题目

题目链接🔗
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

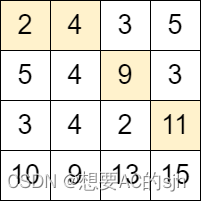
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：

• (0, 0) -> (0, 1).
• (0, 1) -> (1, 2).
• (1, 2) -> (2, 3).

可以证明这是能够移动的最大次数。

示例 2：

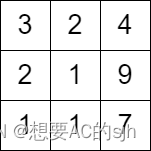
输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10⁵
• 1 <= grid[i][j] <= 10⁶

思路

这道题可以使用动态规划进行完成，题目的意思就是每一次可以移动到右上角或者与右边或者是i右下角，那么我们直接反过来对左边的上中下进行选取即可，$dp[i][j]$表示到当前位置最多要多少步，这个数字取决于前面的$dp[i-1][j-1]$、$dp[i][j-1]$、$dp[i+1][j-1]$，取三者里面的最大值加一赋值给$dp[i][j]$。最后统计最多移动的次数的时候需要注意这样子的计算方法包含中间开始的，而题目要求的是最左边的那一列开始，所以我们可以在统计的时候加上一个条件限制，如果符合题目要求的话移动的次数刚好等于dp数组对应的列下标。

代码

class Solution {
public:int maxMoves(vector<vector<int>>& grid) {int n=grid.size(),m=grid[0].size();vector<vector<int>> dp(n, vector<int>(m, 0));int maxzhi=1;for(int i=0;i<n;++i)dp[i][0]=1;for(int j=1;j<m;++j){for(int i=0;i<n;++i){if(i==0){if(grid[i][j]>grid[i][j-1])dp[i][j]=max(dp[i][j],dp[i][j-1]+1);if(grid[i][j]>grid[i+1][j-1])dp[i][j]=max(dp[i][j],dp[i+1][j-1]+1);}else if(i==n-1){if(grid[i][j]>grid[i-1][j-1])dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);if(grid[i][j]>grid[i][j-1])dp[i][j]=max(dp[i][j],dp[i][j-1]+1);}else{if(grid[i][j]>grid[i-1][j-1])dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1);if(grid[i][j]>grid[i][j-1])dp[i][j]=max(dp[i][j],dp[i][j-1]+1);if(grid[i][j]>grid[i+1][j-1])dp[i][j]=max(dp[i][j],dp[i+1][j-1]+1);}if(j+1==dp[i][j])maxzhi=max(maxzhi,dp[i][j]);}}for(int i=0;i<n;++i){for(int j=0;j<m;++j){cout<<dp[i][j]<<"  ";}cout<<"\n";}return maxzhi-1;}
};

结果