目录
引言
思想
动图
过程展开图
gap的取值
时间复杂度
空间复杂度
代码及其解释
引言
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。
思想
希尔排序是把原数组按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的元素越来越多,当增量减至 1 时,整个数组恰被分成一组,算法便终止。
换种说法,希尔排序是先将整个待排数组分割成若干个子数组,再对子数组分别进行直接插入排序,使整个数组趋近于有序,再对整个数组进行一次直接插入排序。
可以总结其步骤为:
一、用直接插入排序进行预排序——接近有序
二、直接插入排序
动图

过程展开图
图中颜色相同的为一组。
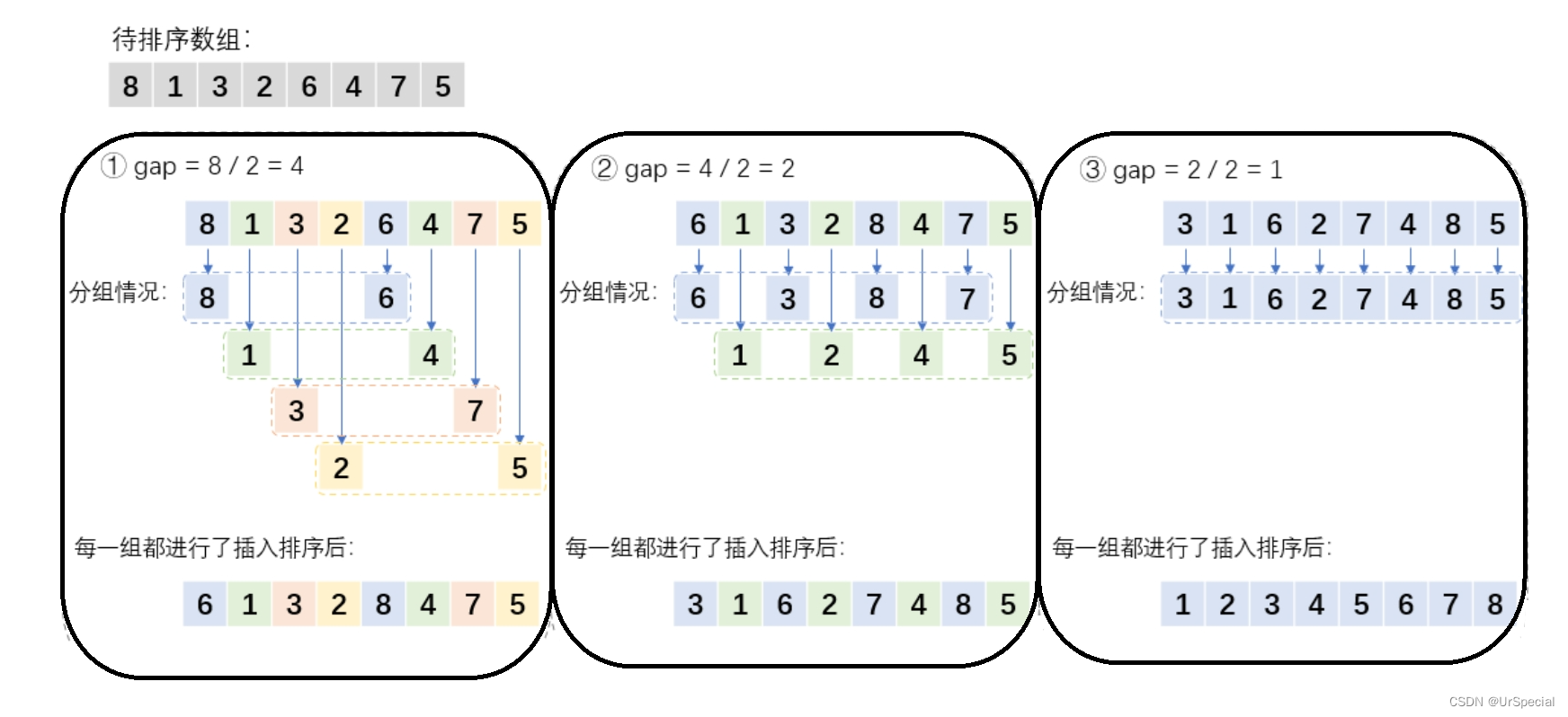
间隔为gap的分为一组,总计gap组。
动态计算增量gap。
从上述过程可以看到,希尔排序的一个特点是:子数组的构成不是简单的“逐段分割”,而是将相隔某个增量(gap)的元素组成一个子数组。相较于直接插入排序,当gap不等于1时,元素不是一步一步的挪动的,而是跳跃式的移动,从而使得在进行最后一趟增量gap = 1的插入排序时,数组已基本有序,只要少量移动和比较即可完成排序。因此希尔排序较直接插入排序的时间复杂度低。
gap的取值
在希尔排序中,增量的取值决定了分组的大小以及排序的效率。一般增量的取值有以下两种:
gap = gap / 2
gap = gap / 3 + 1
确保最后一个增量的值为1。
时间复杂度
希尔排序的分析是一个复杂的问题,因为它的时间是所取“增量”序列的函数,这涉及到一些数学上尚未解决的难题。但有人在大量实验的基础上推出:当n在某个特定范围内,希尔排序所需的比较和移动次数约为n^1.3,所以希尔排序的时间复杂度为O(n^1.3)。
空间复杂度
希尔排序是一种原地排序算法,所以空间复杂度为O(1)。
代码及其解释
#include <stdio.h>void Print(int* a, int n)
{for (int i = 0; i < n; i++) printf("%d ", a[i]);printf("\n");
}void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//动态调整gapfor (int i = 0; i < n - gap; i++)//多组并排{int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}int main()
{int a[] = { 5,1,3,8,0,2,6,4,7 };int n = sizeof(a) / sizeof(int);Print(a, n);ShellSort(a, n);Print(a, n);return 0;
}对多组并排的解释:
下图中,颜色相同的为一组。
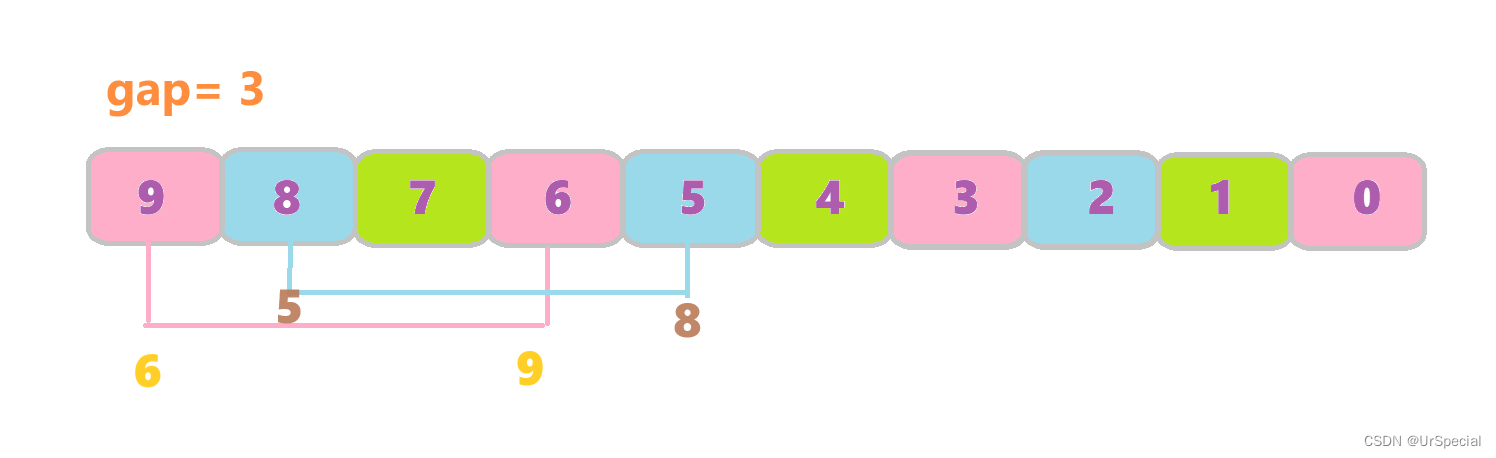
为了说明清楚多组并排,这里拿非多组并排来作为对比。 如果是非多组并排,那么在进行第一趟希尔排序时,就会将粉红色数组中的四个元素看做一个整体进行插入排序,得到的结果为:0 3 6 9。而多组并排呢,是先对9和6进行插入排序得到6 9,接着对下一组(蓝色数组)的8和5进行插入排序,并不是一次性将蓝色数组排好序得到2 5 8,而是不同组之间交替的进行部分插入排序。