Redis中的HyperLogLog以及HyperLogLog原理-编程知识

大家在学习redis的过程中，除了String，list，hash，set，zset这五种基本的数据结构，一定还会接触到几种高级的数据结构，比如bitmap，geo，还有今天我们要说的hyperloglog（下文简称为 HLL）。

HLL是Redis的一种高级数据结构，是统计基数的大杀器。但是我们前提需要了解的是， HLL是一种算法，并非是redis独有的一种数据结构。

HLL的概述：

HLL作为一种基数统计的算法，他的优势在于可以在输入元素的数量或者体积非常非常大时，计算基数所需的空间总是固定的、并且是很小的。

在 Redis 里面，每个 HyperLogLog 键只需要花费 12 KB 内存，就可以计算接近 2^64 个不同元素的基数。这和计算基数时，元素越多耗费内存就越多的集合形成鲜明对比。

但是，因为 HyperLogLog 只会根据输入元素来计算基数，而不会储存输入元素本身，所以 HyperLogLog 不能像集合那样，返回输入的各个元素。

但是统计存在一定的误差，误差率整体较低，标准误差为 0.81%；
误差可以被设置辅助计算因子进行降低。

何为基数？

在数学上，基数或势，即集合中包含的元素的“个数”，是日常交流中基数的概念在数学上的精确化（并使之不再受限于有限情形）。
有限集合的基数，其意义与日常用语中的“基数”相同，例如{{a,b,c}的基数是3。
无限集合的基数，其意义在于比较两个集的大小，例如整数集和有理数集的基数相同；整数集的基数比实数集的小。

基数估计就是在误差可接受的范围内，快速计算基数。

在介绍HyperLogLog的原理之前，请你先来思考一下，如果让你来统计基数，你会用什么方法。

HLL的使用场景：

一般可以bitmap和hyperloglog配合使用，bitmap标识哪些用户活跃，hyperloglog计数一般使用：

统计注册 IP 数
统计每日访问 IP 数
统计页面实时 UV 数
统计在线用户数
统计用户每天搜索不同词条的个数

例如在我们实际开发的过程中，可能会遇到这样一个问题，当我们需要统计一个大型网站的独立访问次数时，该用什么的类型来统计？

如果我们使用 Redis 中的集合来统计，当它每天有数千万级别的访问时，将会是一个巨大的问题。因为这些访问量不能被清空，我们运营人员可能会随时查看这些信息，那么随着时间的推移，这些统计数据所占用的空间会越来越大，逐渐超出我们能承载最大空间。

例如，我们用 IP 来作为独立访问的判断依据，那么我们就要把每个独立 IP 进行存储，以 IP4 来计算，IP4 最多需要 15 个字节来存储信息，例如：110.110.110.110。当有一千万个独立 IP 时，所占用的空间就是 15 bit*10000000 约定于 143MB，但这只是一个页面的统计信息，假如我们有 1 万个这样的页面，那我们就需要 1T 以上的空间来存储这些数据，而且随着 IP6 的普及，这个存储数字会越来越大，那我们就不能用集合的方式来存储了，这个时候我们需要开发新的数据类型 HyperLogLog 来做这件事了。

Redis中 HyperLogLog 命令

1 PFADD key element [element …]
添加指定元素到 HyperLogLog 中。

2 PFCOUNT key [key …]
返回给定 HyperLogLog 的基数估算值。

3 PFMERGE destkey sourcekey [sourcekey …]
将多个 HyperLogLog 合并为一个 HyperLogLog

HLL的原理

HLL是一种优化后的概率算法。

概率算法

目前还没有发现更好的在大数据场景中准确计算基数的高效算法，因此在不追求绝对准确的情况下，使用概率算法算是一个不错的解决方案。概率算法不直接存储数据集合本身，通过一定的概率统计方法预估基数值，这种方法可以大大节省内存，同时保证误差控制在一定范围内。

目前用于基数计数的概率算法包括:

Linear Counting(LC)：早期的基数估计算法，LC在空间复杂度方面并不算优秀，实际上LC的空间复杂度与上文中简单bitmap方法是一样的（但是有个常数项级别的降低），都是O(Nmax)；
LogLog Counting(LLC)：LogLog Counting相比于LC更加节省内存，空间复杂度只有O(log2(log2(Nmax)))；
HyperLogLog Counting(HLL)：HyperLogLog Counting是基于LLC的优化和改进，在同样空间复杂度情况下，能够比LLC的基数估计误差更小。

算法原理：

HyperLogLog 算法来源于论文 HyperLogLog the analysis of a near-optimal cardinality estimation algorithm。

伯努利试验

想要了解 HLL 的原理，先要从伯努利试验说起，伯努利实验说的是抛硬币的事。一次伯努利实验相当于抛硬币，不管抛多少次只要出现一个正面，就称为一回合伯努利实验，回合结束。我们用0表示反面，用1表示正面。
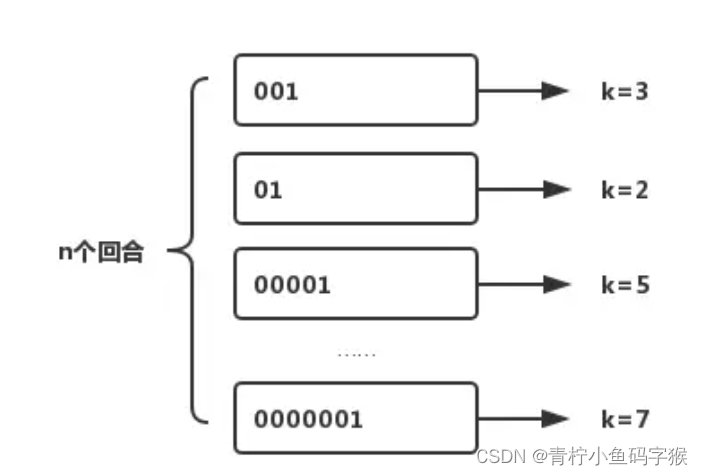
在这里插入图片描述

我们用 k 来表示每回合抛硬币的次数，n 表示回合数量，用 k_max 来表示所有回合中抛硬币的最高次数，最终根据估算发现 n 和 k_max 存在的关系是 n=2^(k_max)。

其实如果稍微懂一点概率论，同学并不用这么麻烦的理解这个概念。我们仅从最大的次数k来看，相当于问，我在抛硬币，连续六次为0，第七次为1，这种0000001的概率为多大？当然很容易理解，每次为1的概率为二分之一，一共的可能结果为二分之一的七次方，而0000001的结果是（1/2）^7，实验样本足够大的情况下，平均每出现一次这种情况，需要2的七次方次实验。则为 n=2^(k_max)。

当然我这是用实验结果来理解实验原理了，很不严谨，只是为了容易理解一些。

但同时我们也发现了另一个问题当试验次数很小的时候，这种估算方法的误差会很大，例如我们进行以下 3 次实验：

第 1 次试验：抛 3 次出现正面，此时 k=3，n=1；
第 2 次试验：抛 2 次出现正面，此时 k=2，n=2；
第 3 次试验：抛 6 次出现正面，此时 k=6，n=3。
对于这三组实验来说，k_max=6，n=3，但放入估算公式明显 3≠2^6。为了解决这个问题 HLL 引入了分桶算法和调和平均数来使这个算法更接近真实情况。

分桶算法

指把原来的数据平均分为 m 份，在每段中求平均数在乘以 m，以此来消减因偶然性带来的误差，提高预估的准确性，简单来说就是把一份数据分为多份，把一轮计算，分为多轮计算。

调和平均数

指的是使用平均数的优化算法，而非直接使用平均数。

例如小明的月工资是 1000 元，而小王的月工资是 100000 元，如果直接取平均数，那小明的平均工资就变成了 (1000+100000)/2=50500‬ 元，这显然是不准确的，而使用调和平均数算法计算的结果是 2/(1/1000+1/100000)≈1998 元，显然此算法更符合实际平均数。

最终的公式如图
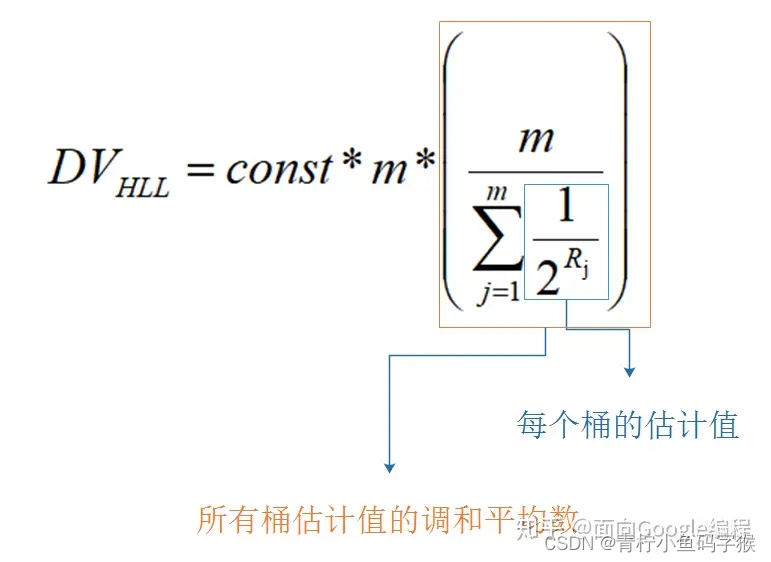
在这里插入图片描述
其中m是桶的数量，const是修正常数，它的取值会根据m而变化。

switch (p) {
case 4:
constant = 0.673 * m * m;
case 5:
constant = 0.697 * m * m;
case 6:
constant = 0.709 * m * m;
default:
constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}

所以综合以上情况，在 Redis 中使用 HLL 插入数据，相当于把存储的值经过 hash 之后，再将 hash 值转换为二进制，存入到不同的桶中，这样就可以用很小的空间存储很多的数据，统计时再去相应的位置进行对比很快就能得出结论，这就是 HLL 算法的基本原理。

Redis中HLL的使用

回到Redis，对于一个输入的字符串，首先得到64位的hash值，
前14位来定位桶的位置（共有 2^14，即16384个桶）。
后面50位即为伯努利过程，每个桶有6bit，记录第一次出现1的位置count，如果count>oldcount，就用count替换oldcount。

了解原理之后，我们再来聊一下HyperLogLog的存储。HyperLogLog的存储结构分为密集存储结构和稀疏存储结构两种，默认为稀疏存储结构，而我们常说的占用12K内存的则是密集存储结构。

密集存储结构

密集存储比较简单，就是连续16384个6bit的串成的位图。由于每个桶是6bit，因此对桶的定位要麻烦一些。

#define HLL_BITS 6 /* Enough to count up to 63 leading zeroes. */
#define HLL_REGISTER_MAX ((1<<HLL_BITS)-1)
/* Store the value of the register at position 'regnum' into variable 'target'.* 'p' is an array of unsigned bytes. */
#define HLL_DENSE_GET_REGISTER(target,p,regnum) do { \uint8_t *_p = (uint8_t*) p; \unsigned long _byte = regnum*HLL_BITS/8; \unsigned long _fb = regnum*HLL_BITS&7; \unsigned long _fb8 = 8 - _fb; \unsigned long b0 = _p[_byte]; \unsigned long b1 = _p[_byte+1]; \target = ((b0 >> _fb) | (b1 << _fb8)) & HLL_REGISTER_MAX; \
} while(0)/* Set the value of the register at position 'regnum' to 'val'.* 'p' is an array of unsigned bytes. */
#define HLL_DENSE_SET_REGISTER(p,regnum,val) do { \uint8_t *_p = (uint8_t*) p; \unsigned long _byte = regnum*HLL_BITS/8; \unsigned long _fb = regnum*HLL_BITS&7; \unsigned long _fb8 = 8 - _fb; \unsigned long _v = val; \_p[_byte] &= ~(HLL_REGISTER_MAX << _fb); \_p[_byte] |= _v << _fb; \_p[_byte+1] &= ~(HLL_REGISTER_MAX >> _fb8); \_p[_byte+1] |= _v >> _fb8; \
} while(0)

如果我们要定位的桶编号为regnum，它的偏移字节量为(regnum * 6) / 8，起始bit偏移为(regnum * 6) % 8，例如，我们要定位编号为5的桶，字节偏移是3，位偏移也是6，也就是说，从第4个字节的第7位开始是编号为3的桶。这里需要注意，字节序和我们平时的字节序相反，因此需要进行倒置。我们用一张图来说明Redis是如何定位桶并且得到存储的值（即HLL_DENSE_GET_REGISTER函数的解释）。

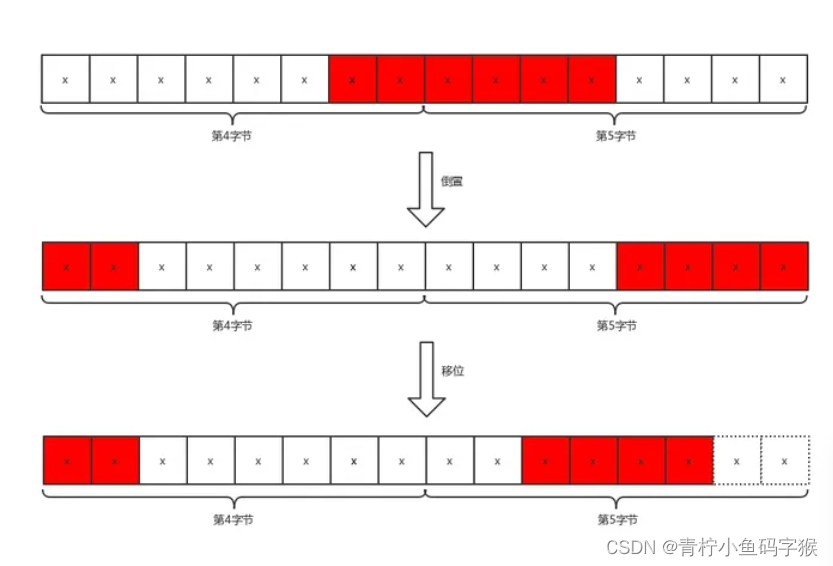
在这里插入图片描述

对于编号为5的桶，我们已经得到了字节偏移_byte和为偏移_fb，b0 >> _fb和b1 << _fb8操作是将字节倒置，然后进行拼接，并且保留最后6位。

稀疏存储结构

你以为Redis真的会用16384个6bit存储每一个HLL对象吗，那就too naive了，虽然它只占用了12K内存，但是Redis对于内存的节约已经到了丧心病狂的地步了。因此，如果比较多的计数值都是0，那么就会采用稀疏存储的结构。

对于连续多个计数值为0的桶，Redis使用的存储方式是：00xxxxxx，前缀两个0，后面6位的值加1表示有连续多少个桶的计数值为0，由于6bit最大能表示64个桶，所以Redis又设计了另一种表示方法：01xxxxxx yyyyyyyy，这样后面14bit就可以表示16384个桶了，而一个初始状态的HyperLogLog对象只需要用2个字节来存储。

如果连续的桶数都不是0，那么Redis的表示方式为1vvvvvxx，即为连续(xx+1)个桶的计数值都是(vvvvv+1)。例如，10011110表示连续3个8。这里使用5bit，最大只能表示32。因此，当某个计数值大于32时，Redis会将这个HyperLogLog对象调整为密集存储。

Redis用三条指令来表达稀疏存储的方式：

ZERO:len 单个字节表示 00[len-1]，连续最多64个零计数值
VAL:value,len 单个字节表示 1[value-1][len-1]，连续 len 个值为 value 的计数值
XZERO:len 双字节表示 01[len-1]，连续最多16384个零计数值

Redis从稀疏存储转换到密集存储的条件是：

任意一个计数值从 32 变成 33，因为VAL指令已经无法容纳，它能表示的计数值最大为 32
稀疏存储占用的总字节数超过 3000 字节，这个阈值可以通过 hll_sparse_max_bytes 参数进行调整。

小结：

HyperLogLog是一种算法，并非redis独有。目的是做基数统计，故不是集合，不会保存元数据，只记录数量而不是数值。
耗空间极小，支持输入非常体积的数据量。核心是基数估算算法，主要表现为计算时内存的使用和数据合并的处理。最终数值存在一定误差。
redis中每个hyperloglog key占用了12K的内存用于标记基数（官方文档）。
pfadd命令并不会一次性分配12k内存，而是随着基数的增加而逐渐增加内存分配；而pfmerge操作则会将sourcekey合并后存储在12k大小的key中，这由hyperloglog合并操作的原理（两个hyperloglog合并时需要单独比较每个桶的值）可以很容易理解。
误差说明：基数估计的结果是一个带有 0.81% 标准错误（standard error）的近似值。是可接受的范围。
Redis 对 HyperLogLog 的存储进行了优化，在计数比较小时，它的存储空间采用稀疏矩阵存储，空间占用很小，仅仅在计数慢慢变大，稀疏矩阵占用空间渐渐超过了阈值时才会一次性转变成稠密矩阵，才会占用12k 的空间。

部分内容转载为：知乎Jackey https://zhuanlan.zhihu.com/p/58519480