C语言分析基础排序算法——归并排序-编程知识

归并排序

递归版本

非递归版本

非递归版本的问题

归并排序小优化

归并排序

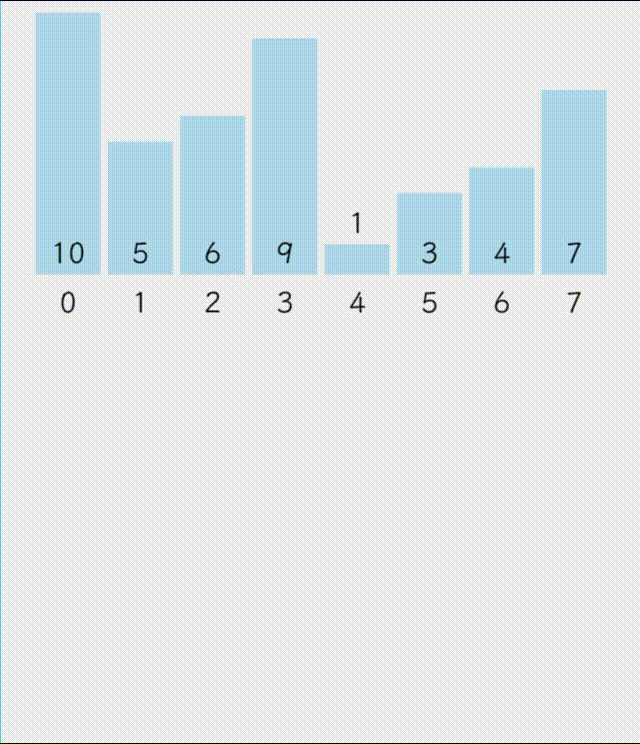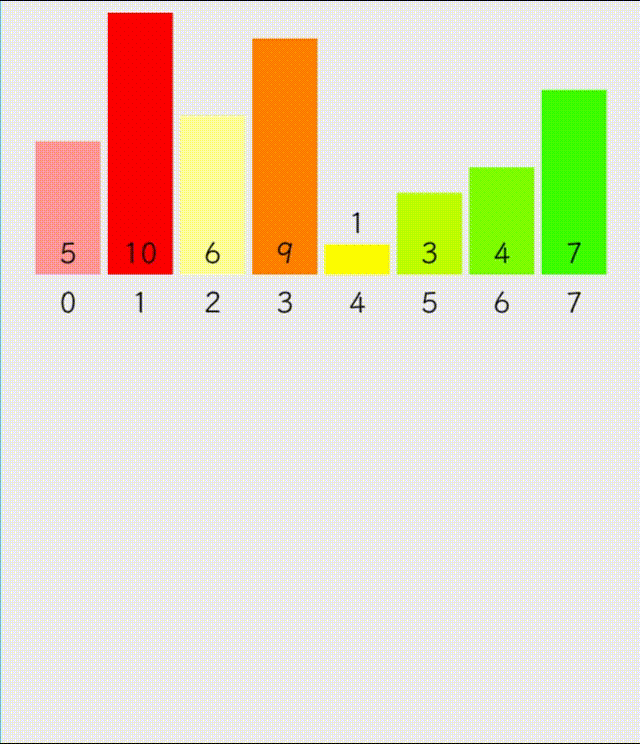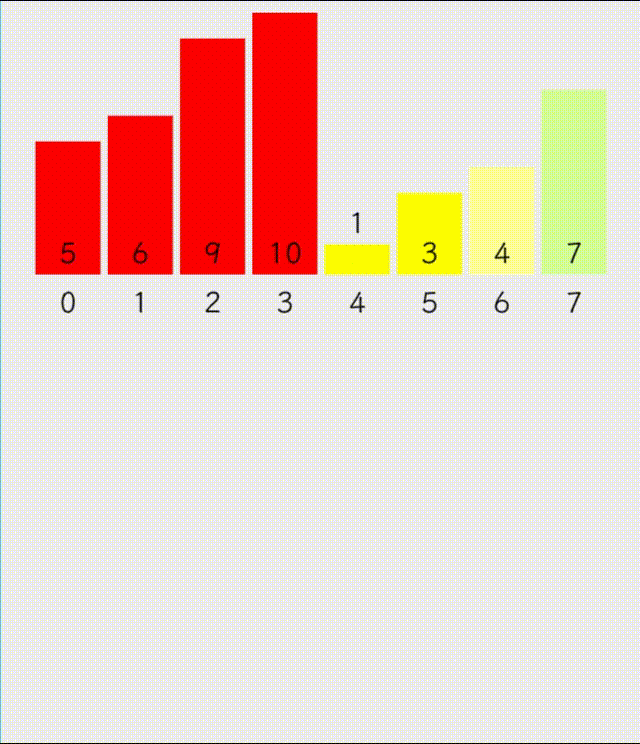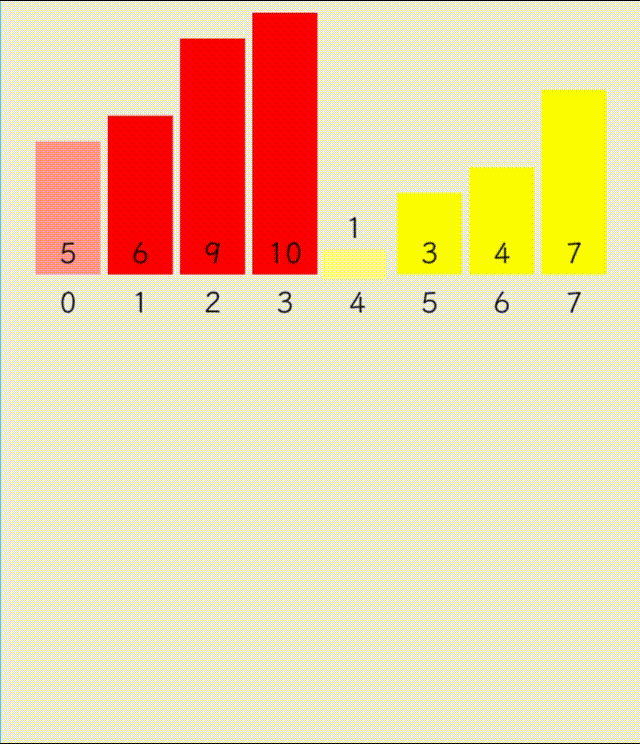
归并排序，分为分治以及合并，分治部分可以使用递归或者非递归完成，归并排序的基本思路是：将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

递归版本

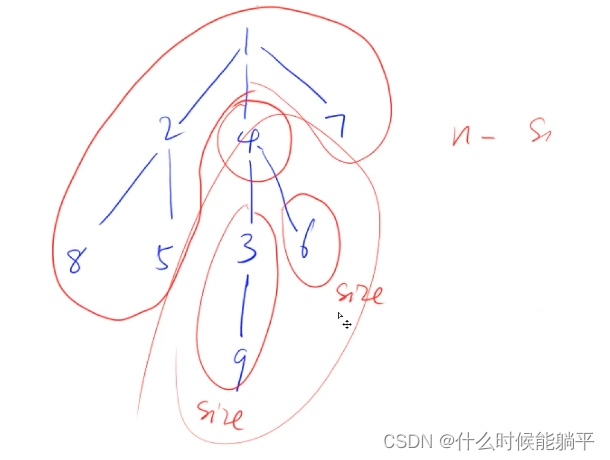
递归版本的归并排序思路如下：先将数组分为不可再分割的只有一个数据的部分，再取小的部分进行尾插，每排序一次就将排序好的数据拷贝到原来的数组中

//以下面的数组为例
int data[] = { 10,5,6,9,1,3,4,7 };

void _MergeSort(int* data, int* tmp, int left, int right)
{//确定递归结束条件if (left == right){return;}//分割数组，首先确定当前数组的中间位置int mid = (left + right) / 2;_MergeSort(data, tmp, left, mid);_MergeSort(data, tmp, mid + 1, right);//取小的数值尾插到tmp数组中int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (data[begin1] < data[begin2]){tmp[i++] = data[begin1++];}else{tmp[i++] = data[begin2++];}}//存在一个数组先走完的情况while (begin1 <= end1){tmp[i++] = data[begin1++];}while (begin2 <= end2){tmp[i++] = data[begin2++];}//排序完之后将tmp数组中的数据拷贝回原来的数组memcpy(data + left, tmp + left, sizeof(int) * (right - left + 1));
}//归并排序递归版
void MergeSort(int* data, int sz)
{//因为需要将排序好的数据重新拷贝到原来的数组中，所以需要开辟数组int* tmp = (int*)malloc(sizeof(int) * sz);assert(tmp);//防止主函数递归导致每次都会重新开辟空间，所以使用子函数_MergeSort(data, tmp, 0, sz - 1);free(tmp);
}

非递归版本

在归并排序中，不使用递归版本时，需要考虑如何对数据进行分堆以及区间的控制，基本思路如下：在循环中，排序间隔为gap的部分数值，再改变gap值，重复前面的步骤，直到最后排序完成。具体思路如下：

//以下面的数组为例
int data[] = { 10,5,6,9,1,3,4,7 };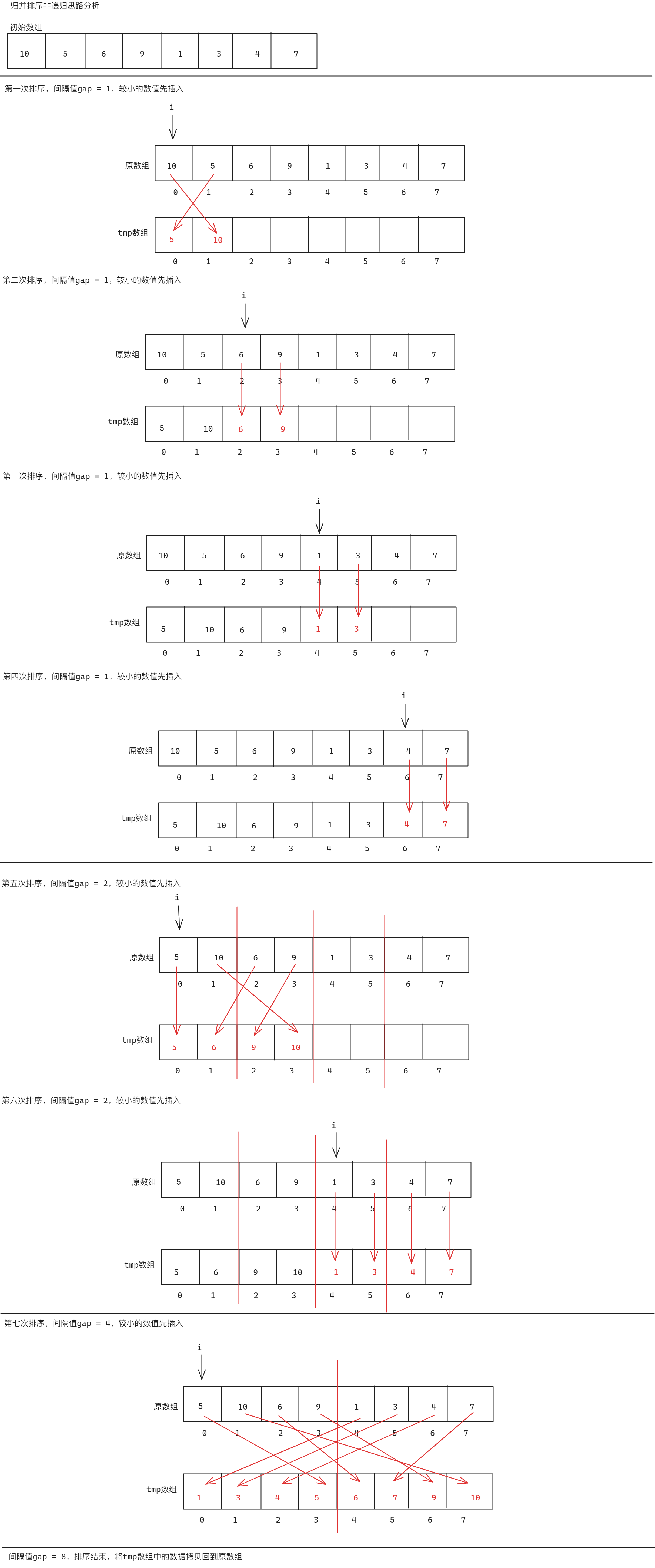

//归并排序非递归版本
void MergeSort_NotRecursion(int* data, int sz)
{//因为需要将排序好的数据重新拷贝到原来的数组中，所以需要开辟数组int* tmp = (int*)malloc(sizeof(int) * sz);assert(tmp);//开始间隔为1int gap = 1;while (gap < sz){//注意i每一次更新为两倍的gap，因为gap只是代表一组有多少个数据，需要i找到下一组for (int i = 0; i < sz; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (data[begin1] < data[begin2]) {tmp[j++] = data[begin1++];}else{tmp[j++] = data[begin2++];}}while (begin1 <= end1){tmp[j++] = data[begin1++];}while (begin2 <= end2){tmp[j++] = data[begin2++];}}memcpy(data, tmp, sizeof(int) * sz);gap *= 2;}free(tmp);
}

非递归版本的问题

但是上面的方法存在一个问题，如果数组的数据不是2的次方个，那么将无法完成排序，存在越界问题

//下面是当数组数据为9个时的越界情况
[0, 0] [1 1]
[2, 2] [3 3]
[4, 4] [5 5]
[6, 6] [7 7]
[8, 8] [9 9][0, 1] [2 3]
[4, 5] [6 7]
[8, 9] [10 11][0, 3] [4 7]
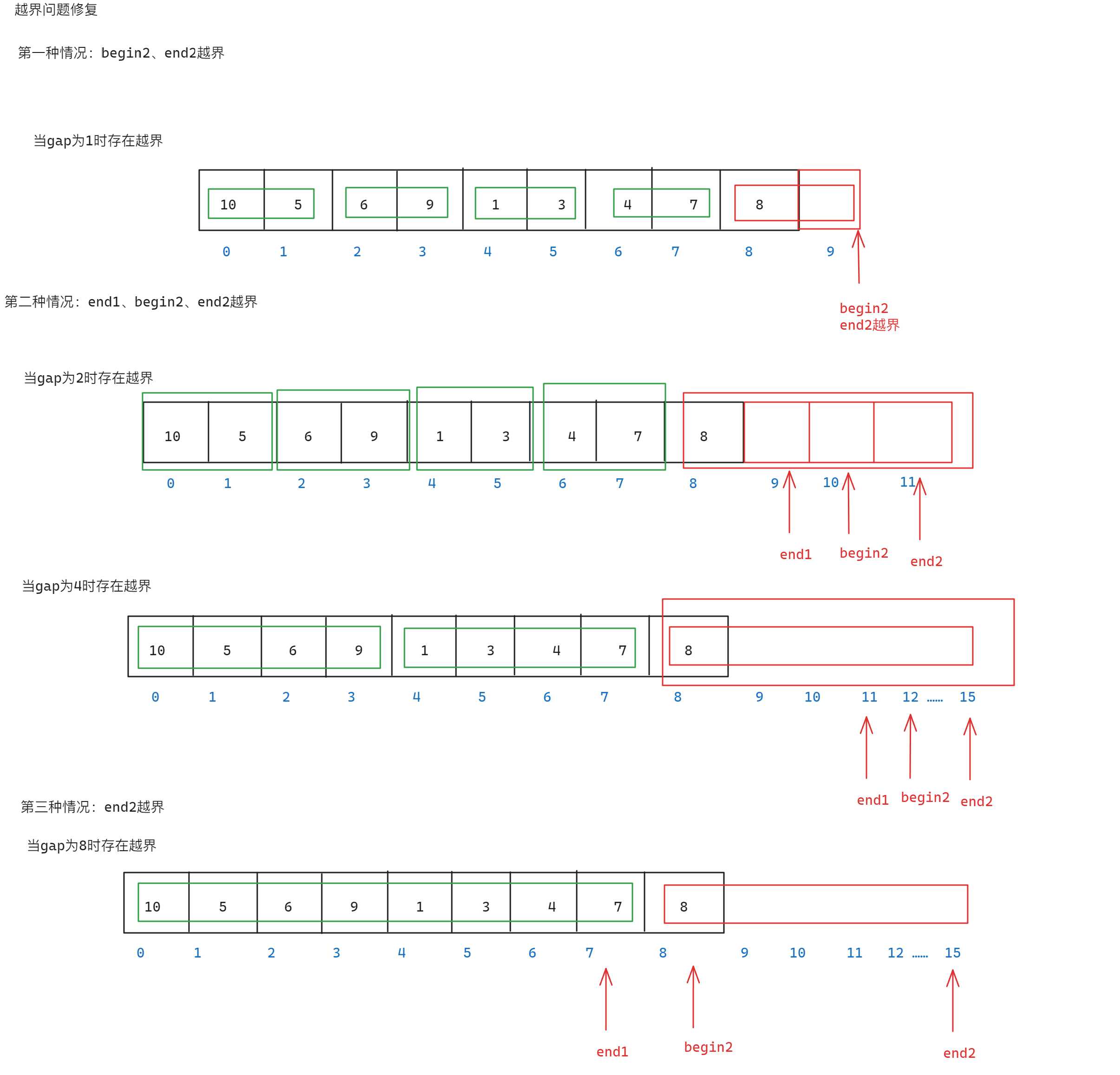
[8, 11] [12 15][0, 7] [8 15]

越界的情况分为三种：

end1、begin2、end2越界，例如[8, 11]、[12, 15]
begin2、end2越界，例如[10, 11]
end2越界，例如[8, 15]

对于上面的问题可以考虑对边界进行修正

第一种解决方法：

当begin2和end1越界时，跳出循环不进行后方数据的调整
当end2越界时，修正end2为数组最后一个元素的位置

//归并排序非递归版本
void MergeSort_NotRecursion(int* data, int sz)
{//因为需要将排序好的数据重新拷贝到原来的数组中，所以需要开辟数组int* tmp = (int*)malloc(sizeof(int) * sz);assert(tmp);//开始间隔为1int gap = 1;while (gap < sz){    //注意i每一次更新为两倍的gap，因为gap只是代表一组有多少个数据，需要i找到下一组for (int i = 0; i < sz; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = begin1;if (begin2 >= sz || end1 >= sz){break;}if (end2 >= sz){end2 = sz - 1;}while (begin1 <= end1 && begin2 <= end2){if (data[begin1] < data[begin2]) {tmp[j++] = data[begin1++];}else{tmp[j++] = data[begin2++];}}while (begin1 <= end1){tmp[j++] = data[begin1++];}while (begin2 <= end2){tmp[j++] = data[begin2++];}memcpy(data + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}

第二种解决方法：

直接对所有区间进行修正，将越界的区间修正成左区间大于右区间的不存在区间，此时不存在的区间将不会进入循环，而存在的区间也是有效区间，直接整体拷贝即可

void MergeSort_NotRecursion1(int* data, int sz)
{int* tmp = (int*)malloc(sizeof(int) * sz);assert(tmp);int gap = 1;while (gap < sz){for (int i = 0; i < sz; i += 2*gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = i;//1. end1 begin2 end2越界if (end1 >= sz){end1 = sz - 1;//修正的不存在区间begin2 = sz;end2 = sz - 1;}else if (begin2 >= sz)//2. begin2 end2 越界{//修正的不存在区间begin2 = sz;end2 = sz - 1;}else if(end2 >= sz)//3. end2越界{end2 = sz - 1;}while (begin1 <= end1 && begin2 <= end2){if (data[begin1] <= data[begin2])//当使用<=时防止出现相等时进行交换，使得排序稳定{tmp[j++] = data[begin1++];}else{tmp[j++] = data[begin2++];}}while (begin1 <= end1){tmp[j++] = data[begin1++];}while (begin2 <= end2){tmp[j++] = data[begin2++];}}memcpy(data, tmp, sizeof(int) * sz);gap *= 2;}free(tmp);
}

归并排序小优化

如果数据的个数特别大时，再让数据一直递归到只有一个数据的一层时会导致递归太深从而栈溢出，可以考虑在只有十个数据递归时采用其他排序算法进行优化，此处可以采用直接插入排序，因为每进行一次递归，数据会被分成两部分，所以当递归到只有十个数据时时，数据个数就已经比较小了

💡

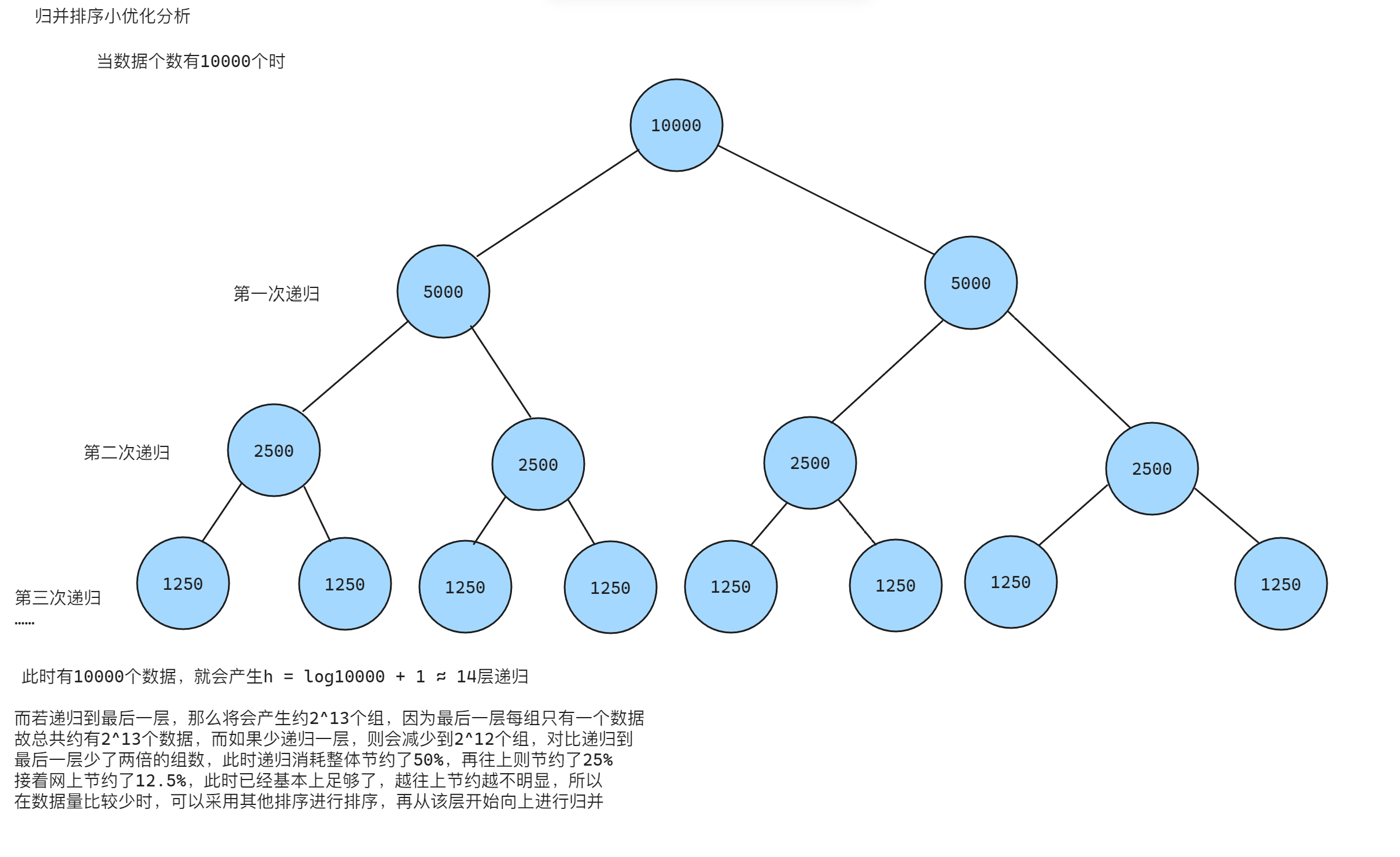
这个优化只是在一定程度上有节省，当数据量特别大时，消耗和递归基本上一致

void InsertSort(int* data, int sz)
{for (int i = 1; i < sz; i++){int tmp = data[i];int end = i - 1;while (end > 0){if (data[end] > tmp){data[end + 1] = data[end];end--;}else{break;}}data[end + 1] = tmp;}
}//归并排序递归版本优化
void _MergeSort_modified(int* data, int* tmp, int left, int right)
{//确定递归结束条件if (left == right){return;}//小区间优化——直接插入排序if ((left - right + 1) < 10){InsertSort(data, left - right + 1);}//分割数组，首先确定当前数组的中间位置int mid = (left + right) / 2;_MergeSort_modified(data, tmp, left, mid);_MergeSort_modified(data, tmp, mid + 1, right);//取小的数值尾插到tmp数组中int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (data[begin1] < data[begin2]){tmp[i++] = data[begin1++];}else{tmp[i++] = data[begin2++];}}//存在一个数组先走完的情况while (begin1 <= end1){tmp[i++] = data[begin1++];}while (begin2 <= end2){tmp[i++] = data[begin2++];}//排序完之后将tmp数组中的数据拷贝回原来的数组memcpy(data + left, tmp + left, sizeof(int) * (right - left + 1));
}//归并排序递归版
void MergeSort_modified(int* data, int sz)
{//因为需要将排序好的数据重新拷贝到原来的数组中，所以需要开辟数组int* tmp = (int*)malloc(sizeof(int) * sz);assert(tmp);//防止主函数递归导致每次都会重新开辟空间，所以使用子函数_MergeSort_modified(data, tmp, 0, sz - 1);free(tmp);
}

归并排序的时间复杂度是 $O(Nlog_{2}{N})$ ，空间复杂度为O(N)，归并排序时稳定排序算法