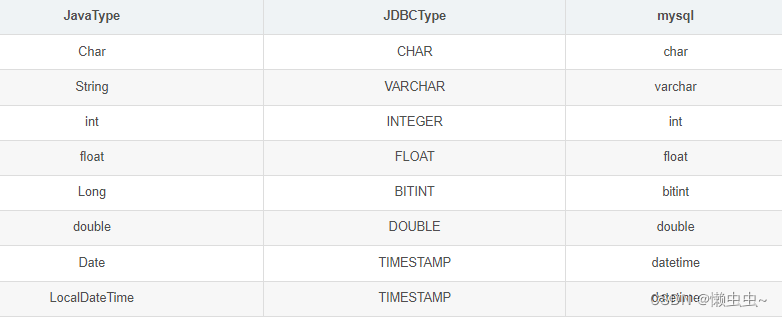
文章目录
- 引言
- 线性规划标准型
- 问题特点
- 单纯形法
引言
很多运筹学的教材都是从线性规划开始的,我平时做算法策略的落地应用时也研发了一部分基于线性规划的技术方案。可以说,如果搞不懂线性规划,很难成为一名优秀的运筹优化算法工程师。
但是我在体系化学习时,却先在其他地方转了一大圈,才来到这里。
主要原因是,这线性规划的原理着实有点难,之前看了很多遍,总有种好像懂了但又没完全懂的挫败感。痛定思痛下终于决定,还是从最简单的无约束问题开始,然后逐渐过渡到有约束问题,以及现在的线性规划问题。
针对无约束优化问题,我细分为一维问题和多维问题,并分别学习了适合解决一维问题的黄金分割法、切线法和进退法等,以及用于解决多维问题的坐标轮转法、最速下降法和拟牛顿法等;针对约束优化问题,相继学习了拉格朗日乘子法和罚函数法。
线性规划问题本质上是一类特殊的约束优化问题,这类优化问题在实际场景中十分常见,同时由于问题的特殊性,也给问题的高效求解带来了新思路。
前面提到过,线性规划对我来说挺难的,只用一篇文章是很难讲清楚。所以打算分成上下两篇:本篇着重讲明白算法原理,下一篇着重研究实践应用。
必须要预警的是,后续内容很枯燥,因为夹杂着非常多的证明和推理过程。我愿意花大量时间在这上面,是希望不仅能知其然,还能知其所以然。不想看细节过程的,可以更多关注整体的逻辑框架:线性规划问题相比一般约束问题的特殊性在哪里–>该特殊性使得线性规划问题具有哪些特点–>基于这些特点,所设计的算法(单纯形法)是如何实现高效求解的。
线性规划标准型
线性规划的标准型矩阵形式为
m i n f ( x ) = c T x s.t. A x = b x ≥ 0 min \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t.} \quad \pmb A\pmb x=\pmb b \\ \quad \quad \ \pmb x ≥ 0 minf(x)=cTxs.t.Ax=b x≥0
也可以写成分量形式
m i n f ( x ) = ∑ j = 1 n c j x j s.t. ∑ j = 1 n a i j x j = b i , i = 1 , 2 , . . . , m x j ≥ 0 , j = 1 , 2 , . . . , n min \quad f(x)=\sum_{j=1}^nc_jx_j \\ \text{s.t.} \quad \sum_{j=1}^na_{ij}x_j=b_i, \quad i=1,2,...,m \\ \quad x_j ≥0 ,\quad j=1,2,...,n\\ minf(x)=j=1∑ncjxjs.t.j=1∑naijxj=bi,i=1,2,...,mxj≥0,j=1,2,...,n
从定义上可以看出,相比一般的约束优化问题,线性规划问题在目标函数、约束条件和变量范围方面都增加了限制:(1)目标函数为线性加和的表达式;(2)约束条件只有线性等式;(3)优化变量大于等于0。
问题特点
增加了上述限制后的线性规划问题,具有哪些特点呢?
先说结论:问题的可行域为凸集–>最优解在凸集的顶点上–>顶点和基本可行解一一对应。
接下来逐个详细说明(证明)。
(1)可行域为凸集。
既然提到凸集,就需要先定义清楚凸集的含义:设 S ∈ R n S \in R^n S∈Rn是 n n n维欧式空间中的一个点集,若对于 x 1 ∈ S , x 2 ∈ S , x 1 ≠ x 2 x_1\in S, x_2 \in S,x_1≠x_2 x1∈S,x2∈S,x1=x2,以及任意 λ ∈ [ 0 , 1 ] \lambda\in [0, 1] λ∈[0,1],必有
λ x 1 + ( 1 − λ ) x 2 ∈ S \lambda x_1+(1-\lambda)x_2 \in S λx1+(1−λ)x2∈S
则称 S S S为凸集。
以下是凸集和非凸集的实例

对于线性规划问题,根据标准型约束的定义
A x 1 = b , x 1 ≥ 0 A x 2 = b , x 2 ≥ 0 \pmb A\pmb x_1=\pmb b, \pmb x_1 ≥ 0\\ \pmb A\pmb x_2=\pmb b, \pmb x_2 ≥ 0 Ax1=b,x1≥0Ax2=b,x2≥0
那么,针对任意 λ ∈ [ 0 , 1 ] \lambda\in[0, 1] λ∈[0,1],假设新变量 x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+(1-\lambda)\pmb x_2 x=λx1+(1−λ)x2,可做如下推导
A [ λ x 1 + ( 1 − λ ) x 2 ] = λ A x 1 + ( 1 − λ ) A x 2 = λ b + ( 1 − λ ) b = b \pmb A[\lambda \pmb x_1+(1-\lambda)\pmb x_2]=\lambda \pmb A\pmb x_1+(1-\lambda)\pmb A\pmb x_2=\lambda \pmb b + (1-\lambda) \pmb b=\pmb b A[λx1+(1−λ)x2]=λAx1+(1−λ)Ax2=λb+(1−λ)b=b
即等式约束成立。
由于 x 1 , x 2 , λ ≥ 0 \pmb x_1,\pmb x_2,\lambda≥0 x1,x2,λ≥0,下式显然也成立
λ x 1 + ( 1 − λ ) x 2 ≥ 0 \lambda \pmb x_1+(1-\lambda)\pmb x_2≥0 λx1+(1−λ)x2≥0
即 x \pmb x x大于等于0亦成立。
所以 x \pmb x x也在可行域内。根据凸集定义,线性规划问题的可行域就是个凸集。
可行域是凸集,有什么好处呢——看下一条结论。
(2)最优值一定在凸集的某个顶点上达到。
顶点这个词在物理世界很容易理解,但为了后续推导,还是需要用数学语言描述清楚这一概念:针对可行域内的 x \pmb x x,如果不存在 λ , x 1 ∈ S , x 2 ∈ S , x 1 ≠ x 2 \lambda,\pmb x_1\in S,\pmb x_2 \in S,\pmb x_1≠\pmb x_2 λ,x1∈S,x2∈S,x1=x2,使得
x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+ (1-\lambda)\pmb x_2 x=λx1+(1−λ)x2
则这个 x \pmb x x为凸集上的顶点。
要证明以上结论,此处使用反证法。
假设凸集的顶点为 x 1 , x 2 , . . . , x k \pmb x_1,\pmb x_2,...,\pmb x_k x1,x2,...,xk,最优解为 x ∗ \pmb x^\ast x∗。因为 x ∗ \pmb x^\ast x∗在可行域的凸集范围内,所以它可以由顶点表示为
x ∗ = ∑ i = 1 k λ i x i \pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb x_i x∗=i=1∑kλixi
式中, λ i ≥ 0 \lambda_i≥0 λi≥0, ∑ i = 1 k λ i = 1 \sum_{i=1}^k\lambda_i=1 ∑i=1kλi=1。 x \pmb x x能被顶点通过线性组合的方式表示,很容易想象,但证明起来有些难,这里就不深入了,有兴趣的可以参考:多面集的表示定理。
上式两边同时左乘 c T \pmb c^T cT
c T x ∗ = ∑ i = 1 k λ i c T x i \pmb c^T\pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_i cTx∗=i=1∑kλicTxi
设 c T x s = min 1 ≤ i ≤ k c T x i \pmb c^T \pmb x_s= \mathop{\text{min}} \limits_{1≤i≤k} \pmb c^T \pmb x_i cTxs=1≤i≤kmincTxi,上式可以做如下推导
c T x ∗ = ∑ i = 1 k λ i c T x i ≥ ∑ i = 1 k λ i c T x s = c T x s ∑ i = 1 k λ i = c T x s \pmb c^T\pmb x^\ast=\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_i≥\sum_{i=1}^k\lambda_i\pmb c^T\pmb x_s=\pmb c^T\pmb x_s\sum_{i=1}^k\lambda_i=\pmb c^T\pmb x_s cTx∗=i=1∑kλicTxi≥i=1∑kλicTxs=cTxsi=1∑kλi=cTxs
但由于 x ∗ \pmb x^\ast x∗是最优解,并且不在顶点上,所以
c T x ∗ < c T x s \pmb c^T\pmb x^\ast < \pmb c^T\pmb x_s cTx∗<cTxs
上述两式互相矛盾,所以假设不成立,即最优解必定在某个顶点上取到。
这个结论的最大优点在于,把决策空间从一个非常大的可行域空间收缩到了可行域的顶点上,而顶点的数量在大部分情况下是比较有限的,这就极大降低了问题求解的复杂度。
这里其实我还有个小疑惑,就是从证明过程来看,好像并不需要目标函数是线性的,是否说明即使目标函数是非线性表达式,最优解依然在顶点上取到?该疑惑目前暂未搞清楚,如有大佬,望不吝赐教。
(3)可行域凸集的顶点和基本可行解一一对应。
已经知道最优解在顶点上了,那顶点的数学表达式是怎样的呢?上述结论告诉我们,顶点就是基本可行解。
接下来,先看一下基本可行解的定义。
A \pmb A A是 m × n m\times n m×n的约束矩阵,可以从中取到一个非奇异方阵 B \pmb B B,然后把剩下列组成一个子阵 N \pmb N N,它们对应的 x \pmb x x分别表示为基变量 x B \pmb x_B xB和非基变量 x N \pmb x_N xN。等式约束可以表示为
B x b + N x N = b \pmb B\pmb x_b+\pmb N\pmb x_N=\pmb b Bxb+NxN=b
令 x N = 0 \pmb x_N=\pmb 0 xN=0,可以求出 x b = B − 1 b \pmb x_b=\pmb B^{-1}\pmb b xb=B−1b,组合 x b \pmb x_b xb和 x N \pmb x_N xN
x = ( B − 1 b , 0 ) T \pmb x=(\pmb B^{-1}\pmb b, 0)^T x=(B−1b,0)T
如果 B − 1 b ≥ 0 \pmb B^{-1}\pmb b≥0 B−1b≥0,则 x \pmb x x被称为基本可行解。
B \pmb B B的维度是 m × m m\times m m×m,理论上至多可以从任意 n n n列中随机选取 m m m列,所以 B \pmb B B的数量上限是 C n m C_n^m Cnm,即基本可行解的数量上限为 C n m C_n^m Cnm个。
上述结论需要分两步进行论证:(1)基本可行解都是顶点;(2)顶点都是基本可行解。
针对第一步,继续使用反证法。
假设某个基本可行解不是顶点,即存在可行解 x 1 , x 2 \pmb x_1,\pmb x_2 x1,x2和 λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ∈[0,1],使得基本可行解 x \pmb x x可以表示为
x = λ x 1 + ( 1 − λ ) x 2 \pmb x=\lambda \pmb x_1+ (1-\lambda)\pmb x_2 x=λx1+(1−λ)x2
将 x \pmb x x写成基变量 x B \pmb x_B xB和非基变量 x N \pmb x_N xN两部分
x B = λ x 1 B + ( 1 − λ ) x 2 B \pmb x_B=\lambda \pmb x_{1B}+ (1-\lambda)\pmb x_{2B} xB=λx1B+(1−λ)x2B
x N = λ x 1 N + ( 1 − λ ) x 2 N \pmb x_N=\lambda \pmb x_{1N}+ (1-\lambda)\pmb x_{2N} xN=λx1N+(1−λ)x2N
x N \pmb x_N xN等式中,因为 x N = 0 , λ > 0 , 1 − λ > 0 , x 1 N ≥ 0 , x 2 N ≥ 0 \pmb x_N=0,\lambda>0,1-\lambda>0,\pmb x_{1N}≥0,\pmb x_{2N}≥0 xN=0,λ>0,1−λ>0,x1N≥0,x2N≥0,故
x N = x 1 N = x 2 N = 0 \pmb x_N=\pmb x_{1N}=\pmb x_{2N}=0 xN=x1N=x2N=0
所以 x 1 \pmb x_1 x1和 x 2 \pmb x_2 x2都是基本可行解,即
B x 1 B = b \pmb B\pmb x_{1B}=\pmb b Bx1B=b
B x 2 B = b \pmb B\pmb x_{2B}=\pmb b Bx2B=b
由于 B \pmb B B为非奇异方阵,所以 B x = b \pmb B\pmb x=\pmb b Bx=b有唯一解,所以
x B = x 1 B = x 2 B \pmb x_B=\pmb x_{1B}=\pmb x_{2B} xB=x1B=x2B
即 x 1 , x 2 \pmb x_1,\pmb x_2 x1,x2就是基本可行解 x \pmb x x,与基本假设不符,所以基本可行解必为可行解的顶点。
针对第二步,还是使用反证法。
假设 x \pmb x x是可行域的顶点,还是先拆解为非零项 x B \pmb x_B xB和零项 x N \pmb x_N xN
B x B = b \pmb B\pmb x_B=\pmb b BxB=b
但由于不是基本可行解,所以对应 B \pmb B B应该是线性相关的,即存在一组非0向量 w \pmb w w,使得
B w = 0 \pmb B\pmb w=\pmb 0 Bw=0
上式乘以系数 δ \delta δ,然后和上上式分别做加法和减法,得到
B ( x B + δ w ) = b B ( x B − δ w ) = b \pmb B(\pmb x_B+\delta \pmb w)=\pmb b\\ \pmb B(\pmb x_B-\delta \pmb w)=\pmb b B(xB+δw)=bB(xB−δw)=b
先令 x B 1 = x B + δ w , x B 2 = x B − δ w \pmb x_B^1=\pmb x_B+\delta \pmb w,\pmb x_B^2=\pmb x_B-\delta \pmb w xB1=xB+δw,xB2=xB−δw,再令 x 1 = ( x B 1 , 0 ) , x 2 = ( x B 2 , 0 ) \pmb x_1=(\pmb x_B^1, \pmb 0),\pmb x_2=(\pmb x_B^2, \pmb 0) x1=(xB1,0),x2=(xB2,0),首先可得
x = 1 2 x 1 + 1 2 x 2 \pmb x=\frac{1}{2}\pmb x_1+\frac{1}{2}\pmb x_2 x=21x1+21x2
同时只要 δ \delta δ足够小
x ± δ w > = 0 \pmb x\pm\delta \pmb w >=\pmb 0 x±δw>=0
即 x 1 \pmb x_1 x1和 x 2 \pmb x_2 x2都是可行解,这说明 x \pmb x x不能是顶点,两者矛盾,所以顶点也必定都是基本可行解。
有了该结论后,理论上,只要算出所有基本可行解的目标函数值,并返回最小值,即得到了最优解。但基本可行解的数量上限是 C n m C_n^m Cnm个,如果 n n n的数量比较大,用遍历的方式寻找最小值貌似就有些吃不消了。
此时大名鼎鼎的单纯形法就该登场了。
单纯形法
同样先给结论,单纯形法最厉害的地方在于:任意给定一个基本可行解后,通过简单的计算评估后,便可以告诉我们,该解是否还有改进空间,如果有,朝着哪个方向改进最好。这样的话,便不再需要去遍历所有基本可行解,所以能极大提升问题求解的效率。
假设已经得到一个基本可行解
x 0 = [ x B , 0 ] = [ B − 1 b , 0 ] \pmb x_0=[\pmb x_B,\pmb 0]=[\pmb B^{-1}\pmb b,\pmb 0] x0=[xB,0]=[B−1b,0]
对应的目标函数值为
f 0 = c B T B − 1 b f_0=\pmb c_B^T\pmb B^{-1}\pmb b f0=cBTB−1b
先把 x 0 \pmb x_0 x0写成基本可行解的通用表达式 [ x B , x N ] [\pmb x_B,\pmb x_N] [xB,xN],代入等式约束
B x B + N x N = b \pmb B\pmb x_B+\pmb N\pmb x_N=\pmb b BxB+NxN=b
移项, x B \pmb x_B xB可以表示为
x B = B − 1 b − B − 1 N x N \pmb x_B=\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N xB=B−1b−B−1NxN
通用表达式结合上式后,再代入目标函数表达式
f = c B T ( B − 1 b − B − 1 N x N ) + c N T x N f=\pmb c_B^T(\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N)+\pmb c_N^T\pmb x_N f=cBT(B−1b−B−1NxN)+cNTxN
重组一下
f = c B T B − 1 b − ( c B T B − 1 N − c N T ) x N f=\pmb c_B^T\pmb B^{-1}\pmb b-(\pmb c_B^T\pmb B^{-1}\pmb N-\pmb c_N^T)\pmb x_N f=cBTB−1b−(cBTB−1N−cNT)xN
上式可以描述为
f = f 0 − ∑ j ∈ R ( z j − c j ) x j f=f_0-\sum_{j\in R}(z_j-c_j)x_j f=f0−j∈R∑(zj−cj)xj
其中, R R R是非基变量集合, z = c B T B − 1 N \pmb z=\pmb c_B^T\pmb B^{-1}\pmb N z=cBTB−1N。
在当前的 x 0 \pmb x_0 x0中,由于 x j = 0 x_j=0 xj=0,即 f f f的后一项为0;所以目标函数能继续降低的基本条件是:至少存在一个 j j j,使得 z j − c j > 0 z_j-c_j>0 zj−cj>0,同时 x j x_j xj也能够从0增加为正数。
z j − c j z_j-c_j zj−cj是参数不是变量,是否存在大于0的 j j j,是无法改变的;但是 x j x_j xj的值理论上是可以优化的,当然该值也不能随意增大,其需要满足的约束是
x B = B − 1 b − B − 1 N x N ≥ 0 \pmb x_B=\pmb B^{-1}\pmb b-\pmb B^{-1}\pmb N\pmb x_N≥0 xB=B−1b−B−1NxN≥0
假设 x k ∈ x N x_k\in \pmb x_N xk∈xN,将从0变为正数(专业术语叫入基),为了保证基本可行解的要求, x B \pmb x_B xB中需要有一个值变为0(专业术语叫出基)
x B = [ x B 1 x B 2 ⋅ ⋅ ⋅ x B m ] = [ b ˉ 1 b ˉ 2 ⋅ ⋅ ⋅ b ˉ m ] − [ y 1 k y 2 k ⋅ ⋅ ⋅ y m k ] x k ≥ 0 \pmb x_B=\left [ \begin{matrix} x_{B1} \\ x_{B2} \\ ··· \\ x_{Bm} \\ \end{matrix} \right ]= \left [ \begin{matrix} \bar b_1 \\ \bar b_2 \\ ··· \\ \bar b_m \\ \end{matrix} \right ]- \left [ \begin{matrix} y_{1k} \\ y_{2k} \\ ··· \\ y_{mk} \\ \end{matrix} \right ]x_k≥0 xB= xB1xB2⋅⋅⋅xBm = bˉ1bˉ2⋅⋅⋅bˉm − y1ky2k⋅⋅⋅ymk xk≥0
其中, b ˉ = B − 1 b \pmb {\bar b}=\pmb B^{-1}\pmb b bˉ=B−1b, y k = B − 1 N k \pmb y_k=\pmb B^{-1}\pmb N_k yk=B−1Nk。为了保证 x B ≥ 0 \pmb x_B≥0 xB≥0, x k x_k xk的最优值是
x k = m i n { b ˉ 1 y 1 k , b ˉ 2 y 2 k , . . . , b ˉ m y m k } x_k=min\{\frac{\bar b_1}{y_{1k}},\frac{\bar b_2}{y_{2k}},...,\frac{\bar b_m}{y_{mk}}\} xk=min{y1kbˉ1,y2kbˉ2,...,ymkbˉm}
基于以上逻辑,我们可以描述为:如果存在 k k k,使得 z k − c k > 0 z_k-c_k>0 zk−ck>0,此时令 x k = m i n b ˉ i y i k x_k=min{\frac{\bar b_i}{y_{ik}}} xk=minyikbˉi,可以使得目标函数值得到最大程度的降低。
这里还有一些特殊情况需要单独考虑:
(1) 所有 z i − c i ≤ 0 z_i-c_i≤0 zi−ci≤0,即 f ≤ f 0 f≤f_0 f≤f0,此时当前基本可行解就是最优解。
(2) x k = m i n b ˉ i y i k x_k=min{\frac{\bar b_i}{y_{ik}}} xk=minyikbˉi中, b ˉ i \bar b_i bˉi是原基本可行解的分量,所以其值≥0是毋庸置疑的;但是 y i k y_{ik} yik的大小是不确定的,如果其部分值≤0,结合 x k ≥ 0 x_k≥0 xk≥0的自身约束,原有流程还能继续进行;但如果全部≤0,流程就无法再继续进行了,事实上,即使 x k x_k xk取无穷大, x B = b ˉ − y k x k ≥ 0 \pmb x_B=\pmb {\bar b}-\pmb y_kx_k≥0 xB=bˉ−ykxk≥0的约束依然能够满足, f f f将变为无穷小,所以此时原问题无下界,不存在最小值。
综上,单纯形法的基本步骤可以概述为:
(1) 将所给的线性规划问题化为标准型;
(2) 找出一个初始基本可行解。
(3) 检验 z i − c i z_i-c_i zi−ci和 b ˉ i y i k \frac{\bar b_i}{y_{ik}} yikbˉi,判断当前解的状态:最优解或不存在最优解,则退出;否则继续。
(4) 找到最佳 k k k,更新 x B \pmb x_B xB,得到一个新的基本可行解,转至(3)。
好了,总算是搞明白求解线性规划问题的算法原理了。