【Godot4.2】Rect2拓展——mRect2类-编程知识

概述

Rect2存在一些问题，比如难以获取除position、end和center之外的其他点。虽然计算并不复杂，就是简单的向量加减。但每次手动计算则比较麻烦。
其实在ShapePoints静态函数库中，已经尝试返回矩形的四个顶点，用于绘制矩形。

# 返回矩形的顶点
# 注意：以(0,0)为几何中心
static func rect(size:Vector2) -> PackedVector2Array:var points:PackedVector2Array = [-size/2,-size/2 + Vector2.RIGHT * size.x,size/2,-size/2 + Vector2.DOWN * size.y,-size/2]return points

mRect2要做的是基于一个Rect2，快速返回九个位置点。

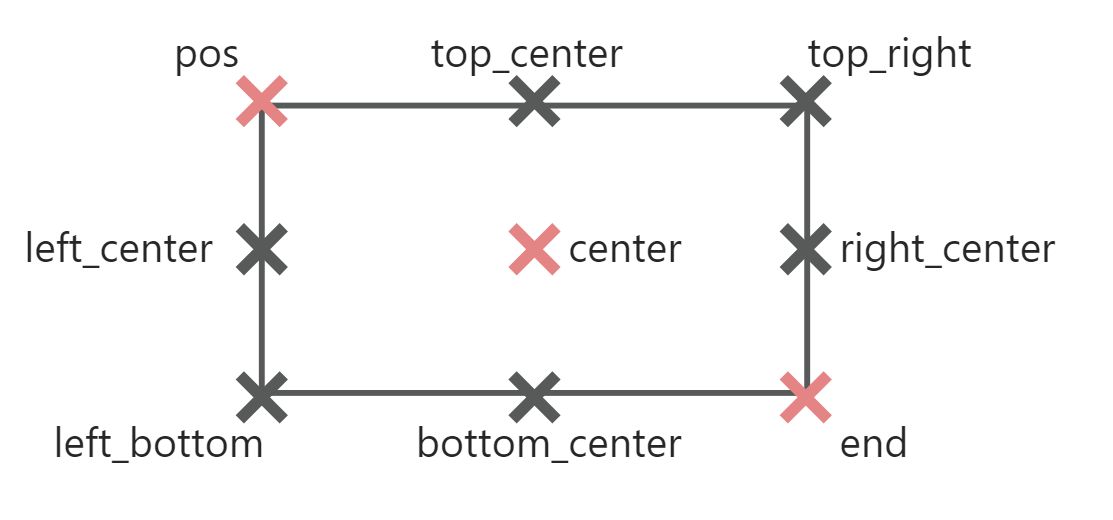
源代码

基于简单的思想，简单的实现了mRect2。

# ========================================================
# 名称：mRect2
# 类型：自定义类
# 作者：巽星石
# Godot版本：4.1-stable (official) --> v4.2.1.stable.official [b09f793f5]
# 基于Rect2获取更多的边角点信息。
# 创建时间：2023-07-09 17:46:49
# 最后修改时间：2024年3月21日21:09:52
# ========================================================class_name mRect2var _rect:Rect2# =================================== 构造 ===================================
func _init(rect:Rect2):_rect = rect# =================================== 静态方法 ===================================
# 根据position和size构造
static func by_size(position:Vector2,size:Vector2) -> mRect2:var rect = Rect2(position,size)return mRect2.new(rect)# 根据x,y,width,height 构造
static func by_xywh(x:float,y:float,width:float,height:float) -> mRect2:var rect = Rect2(x,y,width,height)return mRect2.new(rect)# =================================== 方法 ===================================
## 矩形 - 左上角 - 坐标
func top_left() -> Vector2:return _rect.position## 矩形 - 顶边中心 - 坐标
func top_center() -> Vector2:return _rect.position + Vector2.RIGHT * (_rect.size.x/2)## 矩形 - 顶边中心 - 坐标
func top_right() -> Vector2:return _rect.position + Vector2.RIGHT * _rect.size.x## 矩形 - 左边中心 - 坐标
func left_center() -> Vector2:return _rect.position + Vector2.DOWN * (_rect.size.y/2)## 矩形 - 矩形中心 - 坐标
func center() -> Vector2:return _rect.get_center()## 矩形 - 右边中心 - 坐标
func right_center() -> Vector2:return  _rect.get_center() + Vector2.RIGHT * (_rect.size.x/2)## 矩形 - 左下角 - 坐标
func left_bottom() -> Vector2:return _rect.position + Vector2.DOWN * _rect.size.y## 矩形 - 底边中心 - 坐标
func bottom_center() -> Vector2:return _rect.get_center()  + Vector2.DOWN * (_rect.size.y/2)## 矩形 - 右下角 - 坐标
func right_bottom() -> Vector2:return  _rect.end## 矩形 - 四个角坐标点 - 数组
## 可同于绘制矩形
func corners() -> PackedVector2Array:return [top_left(),top_right(),right_bottom(),left_bottom()]# 返回向外扩展一定距离的四个角顶点
func expend_corners(length:float) -> PackedVector2Array:var arr:PackedVector2Arrayvar v1 = - Vector2.ONE * lengtharr.append(top_left() + v1)arr.append(top_right() + v1.rotated(deg_to_rad(90)))arr.append(right_bottom() + v1.rotated(deg_to_rad(180)))arr.append(left_bottom() + v1.rotated(deg_to_rad(270)))return arr# 返回向外扩展一定距离的四个角顶点水平和垂直延伸出一定距离的点坐标
func expend_corners_lines(length:float,a:float = 10.0,b:float =10.0) -> PackedVector2Array:var arr:PackedVector2Arrayvar v1 = - Vector2.ONE * lengthvar p1 = top_left() + v1  # 第一个扩展点var v_a1 = Vector2.RIGHT * a  # 水平向量var v_b1 = Vector2.DOWN * b   # 垂直向量arr.append_array([p1,p1+v_a1]) # 添加水平线arr.append_array([p1,p1+v_b1]) # 添加垂直线# 右上角点var rad2 = deg_to_rad(90)var p2 = top_right() + v1.rotated(rad2)arr.append_array([p2,p2 - v_a1]) # 添加水平线arr.append_array([p2,p2 + v_b1]) # 添加垂直线# 右上角点var rad3 = deg_to_rad(180)var p3 = right_bottom() + v1.rotated(rad3)arr.append_array([p3,p3 - v_a1]) # 添加水平线arr.append_array([p3,p3 - v_b1]) # 添加垂直线# 右上角点var rad4 = deg_to_rad(270)var p4 = left_bottom() + v1.rotated(rad4)arr.append_array([p4,p4 + v_a1]) # 添加水平线arr.append_array([p4,p4 - v_b1]) # 添加垂直线return arr## 返回矩形对应的9个点 - 数组
func points() -> PackedVector2Array:return [top_left(),top_center(),top_right(),right_center(),right_bottom(),bottom_center(),left_bottom(),left_center(), center()]

使用

可以通过以下3种方式构建mRect2实例：

可以通过给mRect2的new()传入一个Rect2类型来创建mRect2实例
可以通过by_size静态方法，基于position和size2个参数创建mRect2实例
可以通过by_xywh静态方法，基于x、y、width和height4个参数创建mRect2实例

var rect = mRect2.new(Rect2.new())
var rect = mRect2.by_size(Vector2(100,100),Vector2(300,400))
var rect = mRect2.by_xywh(100,100,300,400)

快速获取矩形的某个特殊点坐标

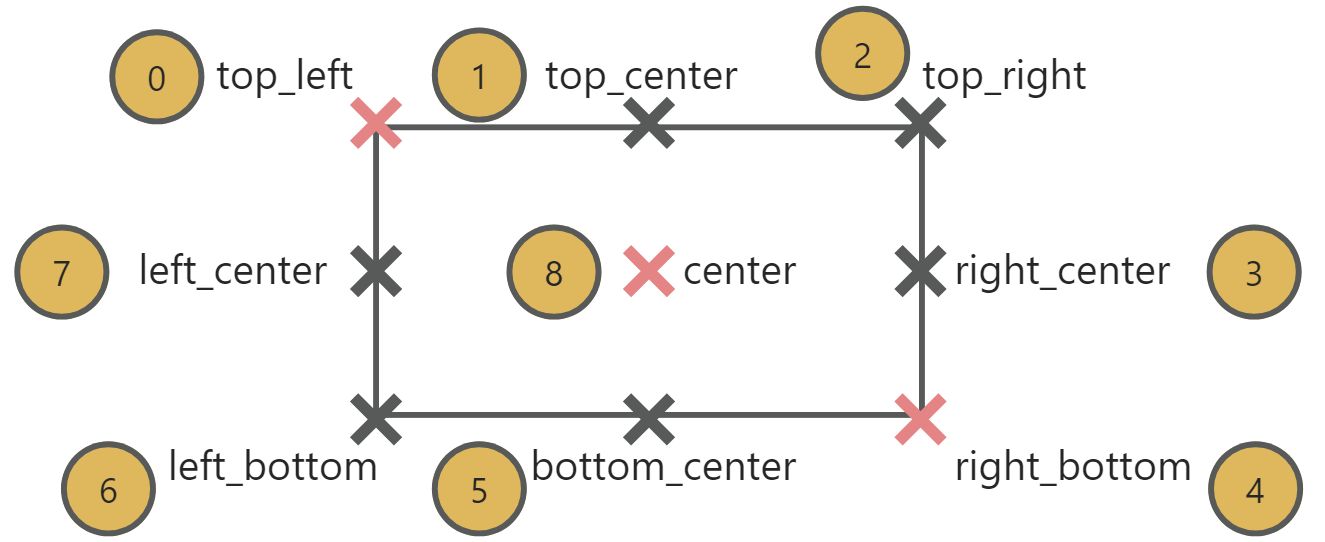
mRect2中，将一个矩形的4个顶点、4个边的中点以及矩形中心点，共9个特殊点，从左上角开始，顺时针存入points方法所返回的数组中，你可以通过points()[下标]形式获取相应的点。
或者也可以通过对应名称的方法获取。

# 获取安全矩形
var rect = mRect2.new(get_draw_safety_rect())
print(rect.top_left())       # 左上角 -- 等价于rect.points()[0]
print(rect.top_center())     # 上边中点 -- 等价于rect.points()[1]
print(rect.top_right())      # 右上角	 -- 等价于rect.points()[2]
print(rect.right_center())   # 右边中点 -- 等价于rect.points()[3]
print(rect.right_bottom())   # 右下角	 -- 等价于rect.points()[4]
print(rect.bottom_center())  # 下边中点 -- 等价于rect.points()[5]
print(rect.left_bottom())    # 左下角	 -- 等价于rect.points()[6]
print(rect.left_center())    # 左边中点 -- 等价于rect.points()[7]
print(rect.center())         # 中点 -- 等价于rect.points()[8]

绘制矩形的9个特殊点

我们创建如下场景：

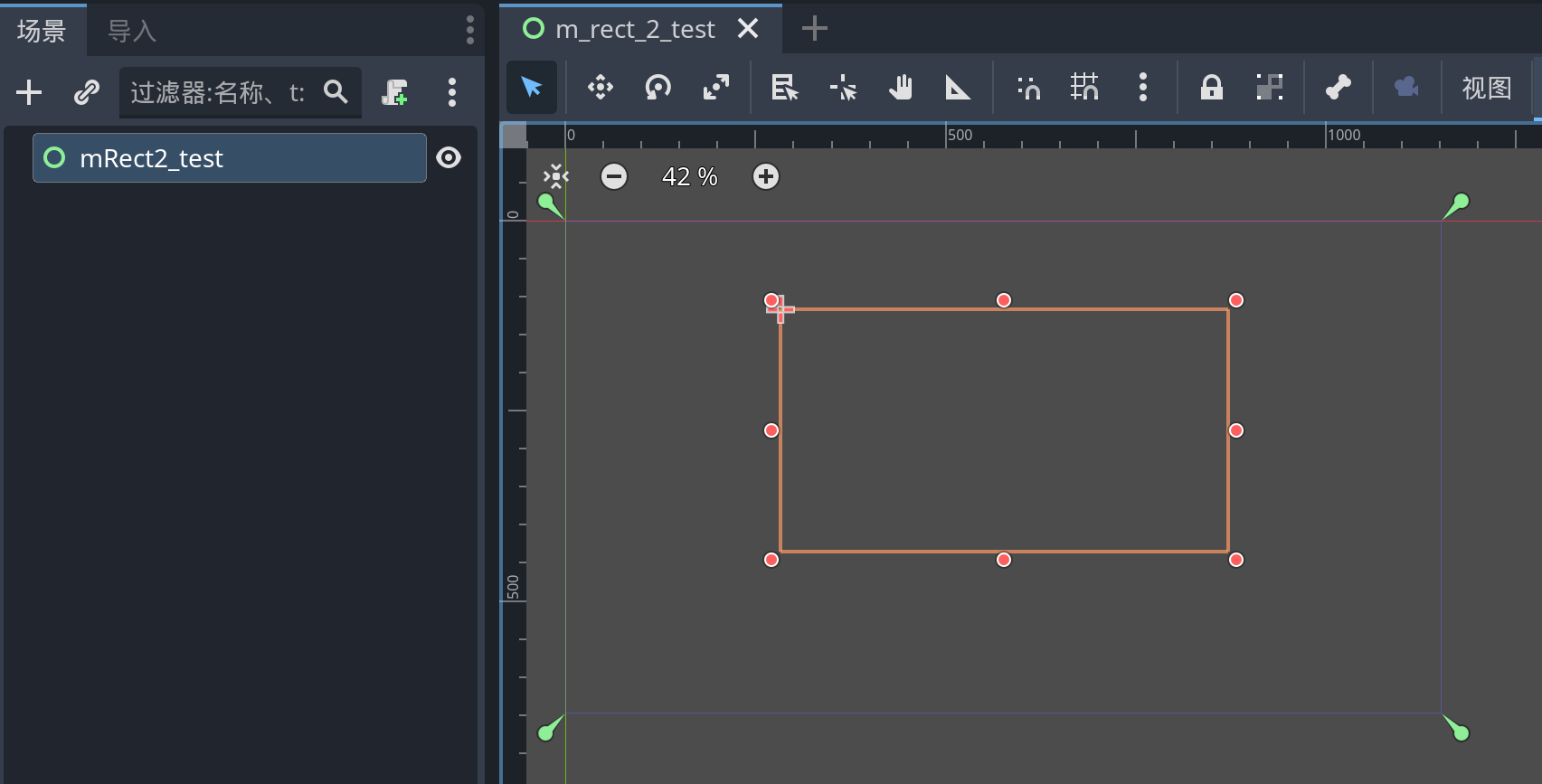
为根节点添加代码如下：

@tool
extends Controlfunc _draw():# 获取安全矩形var rect = mRect2.new(get_draw_safety_rect())# 绘制边框矩形draw_rect(get_draw_safety_rect(),Color.GREEN_YELLOW,false,1)# 绘制9个特殊点for point in rect.points():draw_circle(point,5,Color.GOLDENROD)# 获取绘制函数能正确使用的控件Rect2
func get_draw_safety_rect() -> Rect2:var rect = get_rect()return Rect2(rect.position - position,rect.size/scale)

可以看到绘制出的效果：

之所以大费周章的编写方法获取这9个点的位置，是因为，基于它们我们可以对矩形进行一定的修饰。比如在矩形外四个角上绘制选择框等。

在矩形的四个角外绘制特殊纹理

获取四个角向外扩展一定距离后的坐标

@tool
extends Controlfunc _draw():# 获取安全矩形var rect = mRect2.new(get_draw_safety_rect())draw_rect(get_draw_safety_rect(),Color.YELLOW_GREEN,false,2)# 获取和绘制向外扩展的四个角顶点var points = rect.expend_corners(20) # 获取向外扩展20像素后的四个角顶点坐标for point in points:draw_circle(point,5,Color.YELLOW)# 获取绘制函数能正确使用的控件Rect2
func get_draw_safety_rect() -> Rect2:var rect = get_rect()return Rect2(rect.position - position,rect.size/scale)

通过expend_corners可以获取四个角向外扩展一定距离的坐标，从而可以在矩形的4个角之外，绘制特殊的形状。这里简单的绘制了4个圆点：

获取四个角向外扩展一定距离后水平和垂直延伸的线段

expend_corners_lines更近一步，获取从扩展点水平和垂直延伸出给定长度的线段的坐标。
使用draw_multiline就可以直接绘制。

@tool
extends Controlfunc _draw():# 获取安全矩形var rect = mRect2.new(get_draw_safety_rect())draw_rect(get_draw_safety_rect(),Color.YELLOW_GREEN,false,2)# 获取和绘制向外扩展的四个角顶点var points = rect.expend_corners_lines(20,50,60) # 获取向外扩展20像素后的四个角顶点坐标draw_multiline(points,Color.YELLOW,2)# 获取绘制函数能正确使用的控件Rect2
func get_draw_safety_rect() -> Rect2:var rect = get_rect()return Rect2(rect.position - position,rect.size/scale)

绘制后的效果：

应用之一就是为Sprite2D等绘制选中框。

@tool
extends Sprite2Dfunc _draw():var rect = mRect2.new(get_rect())# 获取和绘制向外扩展的四个角顶点var points = rect.expend_corners_lines(20,50,60) # 获取向外扩展20像素后的四个角顶点坐标draw_multiline(points,Color.YELLOW,2)