前言:剑指offer刷题系列
问题:
桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。
示例:
输入:[4,2,1]
输出:4
解释:第一堆力扣币最少需要拿 2 次,第二堆最少需要拿 1 次,第三堆最少需要拿 1 次,总共 4 次即可拿完。
思路:
题目说的有点曲折,可以稍微修改题目看起来更好理解。即当给出一个包含不同面额硬币的列表coins,如何计算出最少需要多少个硬币来凑成一个给定的总金额。可以使用贪心算法来解决这个问题,一次可以去1次或2次,那默认每次都按最大数量取硬币。
即我的思想是尽可能每次多地拿取每个硬币,因为使用一个硬币只需要一次操作,而不使用硬币需要两次操作。所以,对于每个硬币,我们将其面额加一后再除以2,得到需要的硬币数量,并累加到count中,最后输出count为进行操作的次数。
这个算法的时间复杂度是O(N),其中N是硬币的数量,因为我们只需遍历一次硬币列表。
空间复杂度:O(1)
基于上述思考,代码如下:
class Solution:def minCount(self, coins: List[int]) -> int:count = 0for coin in coins:count += (coin + 1) // 2return count
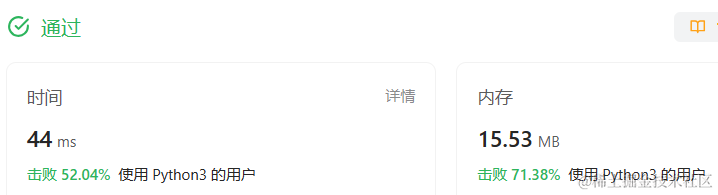
执行结果如下图:
时间运行速度还行,内存消耗还不错。
学到的知识点:
- 贪心算法(Greedy Algorithm): 这段代码使用了贪心算法的思想,即每次选择当前情况下最优的解决方案,而不考虑全局的最优解。在这个例子中,我们每次尽量多地使用每个硬币,以最小化所需的硬币数量,贪心算法在这里的局部最优解也是全局最优解。
- 整数除法和取整: 代码中使用了
(coin + 1) // 2来进行整数除法,这是一种常见的计算方法,可以得到除法结果的整数部分,也可以使用python的ceil函数实现相同操作。