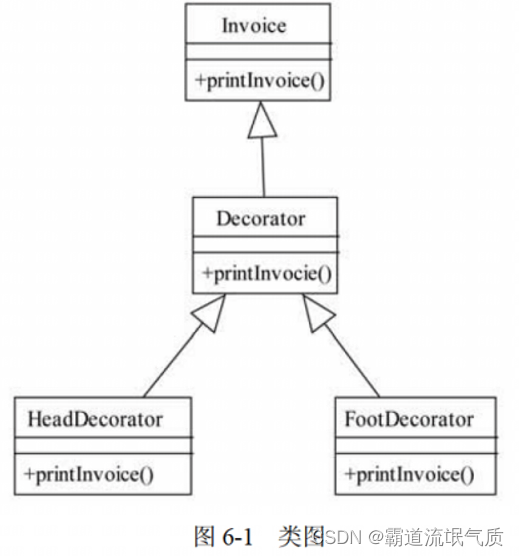
上次总结了Dijkstra算法的案例原理与代码,本文分享第二种比较基础且易懂的方法为Floyd算法,该算法可以有效正确地处理有向图的最短路径问题,与Dijkstra算法不同,Floyd算法是一种动态规划算法,对于稠密图效果显著。原理简单高效,其可以计算任意两个节点的最小距离,时间复杂度为O(n3)。
一、Floyd算法讲解:
本文讲解案例来自于古月学院,该篇也是对笔者学习内容的总结,有需要的朋友可以直接跳转到课程。其算法流程图如下,可能刚开始看着有点懵(笔者也是),没事听着笔者讲解下很容易可以理解的。
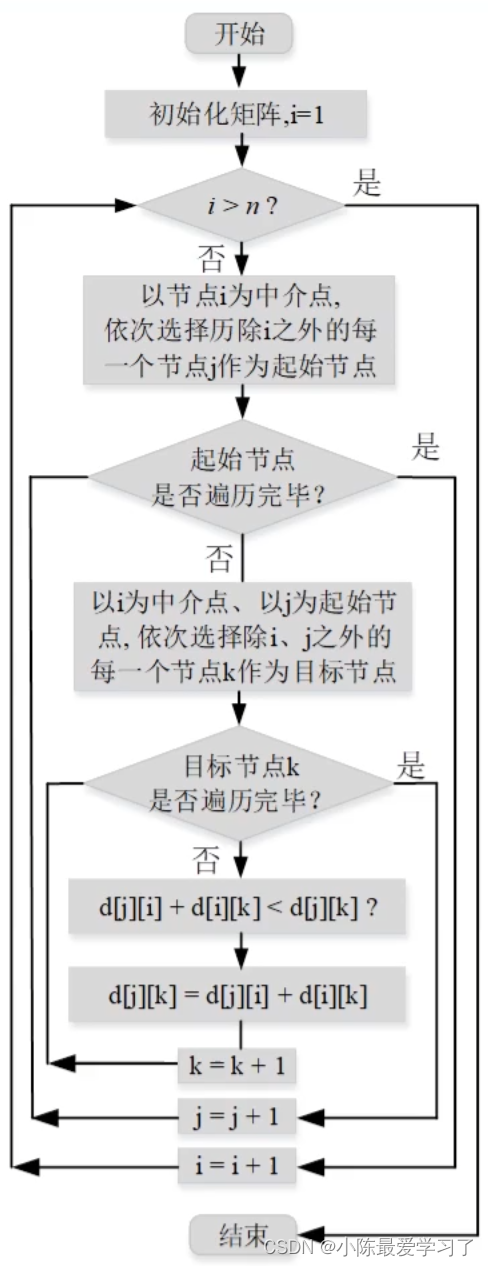
1. 初始化:
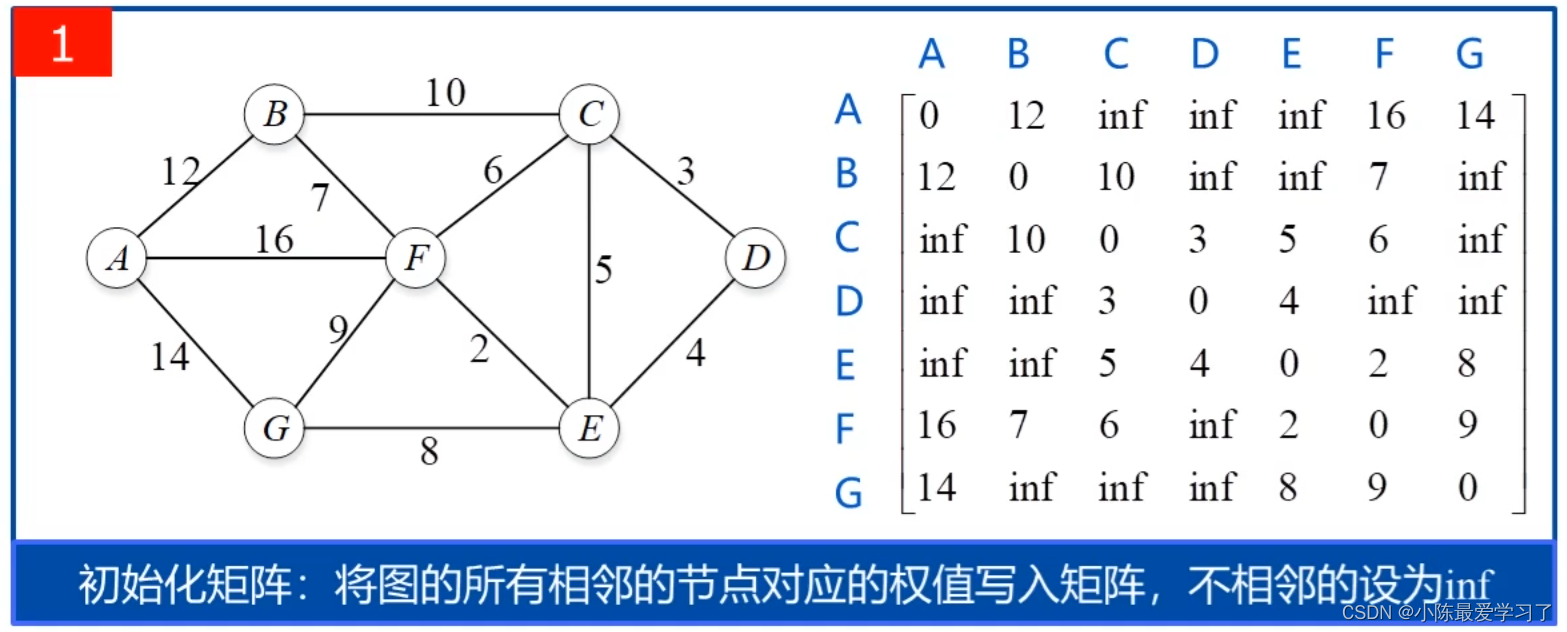
如上图所示,假如有稠密图如上,共有ABCDEFG总共7个节点,故此时上述流程图的n=7,初始化一个7*7的矩阵,记录每两个节点的距离,如第一行第一列的元素代表A到A的距离,为0,看图将矩阵填好,有直接连接的节点填的就是其距离,如BC直接相连,距离如上图记为10,同理CB也为10。无直接连接关系的记为inf代表无穷大的范围。
2. 循环更新代价矩阵(第一个循环):
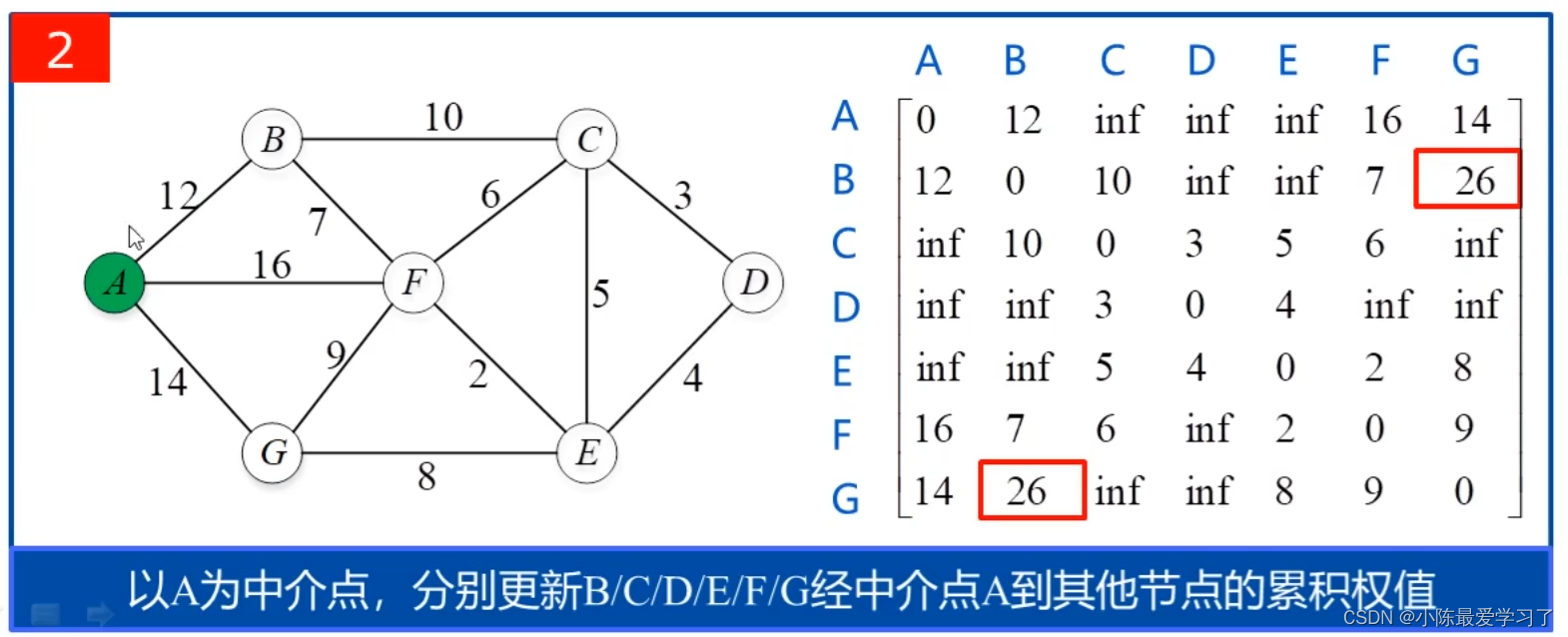
初始化完成后我们进入第一个循环,此时i=1(按顺序排序,i=1234567分别为ABCDEFG为中介点的情况),此时我们需要以A为中间点,此时选取除A外的任一节点,并计算该节点与除开A点与该点以外的任一点的距离,如此时选取B点,计算B点到除A外的任一点的距离,如计算B到C的距离,经过A到达C的距离为AC距离加上BA距离,此时为inf+10>10不更新;下一个计算B到D的距离,B与D不直接连接故为inf,而B经过A到C的距离为AC距离+BD距离为inf+12=inf,故不用更新,同理可以更新B到E、F的距离,当B通过A到达E、F点的距离<B直接连接E、F的距离时,更新矩阵中的距离值。如上述所示,计算B经过A连接到G的距离为BA+AG=12+14=26 < inf(B直接连接G的距离,因为没有直接连接所以为inf),此时更新B到G的距离。
更新完A点为中介点时B到达其他点的距离后,更新以A为中介点C到达其他任意点的距离,以此类推,计算D、E、F、G以A为中介点到达其他节点的距离。上述过程相当于三层循环,此时结束了A点作为中介点的情况。
描述很绕,笔者画了一个图方便大家理解:
3. 循环更新代价矩阵(第二个循环):
此时以A点为中介点的遍历结束,i+1=2,此时中介点为B,更新A、C、D、E、F、G以B为中介点到达彼此的距离,并与直接相连接的距离进行比较,当经过中介点B的距离<直接连接的距离时,更新该值。
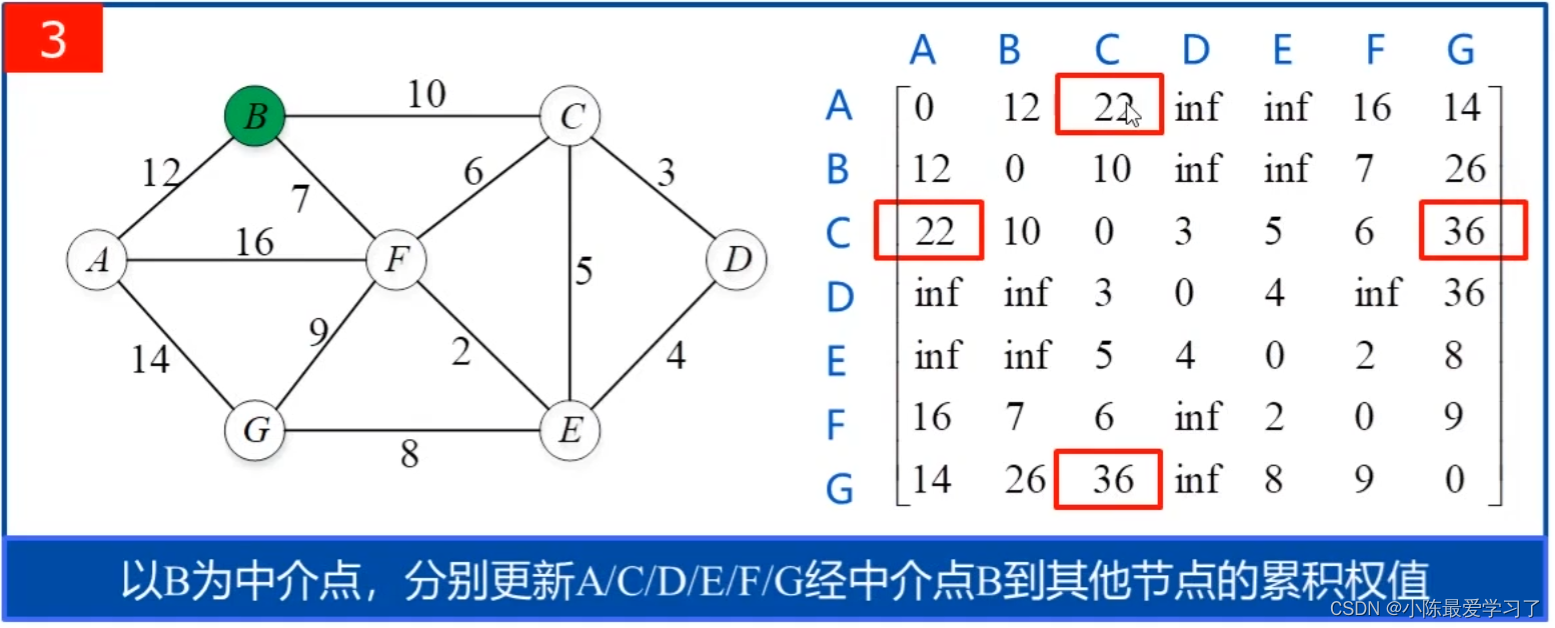
4. 循环更新代价矩阵(第三个循环):
以C点为中介点,更新A、B、D、E、F、G以C为中介点到达彼此的距离,以此类推
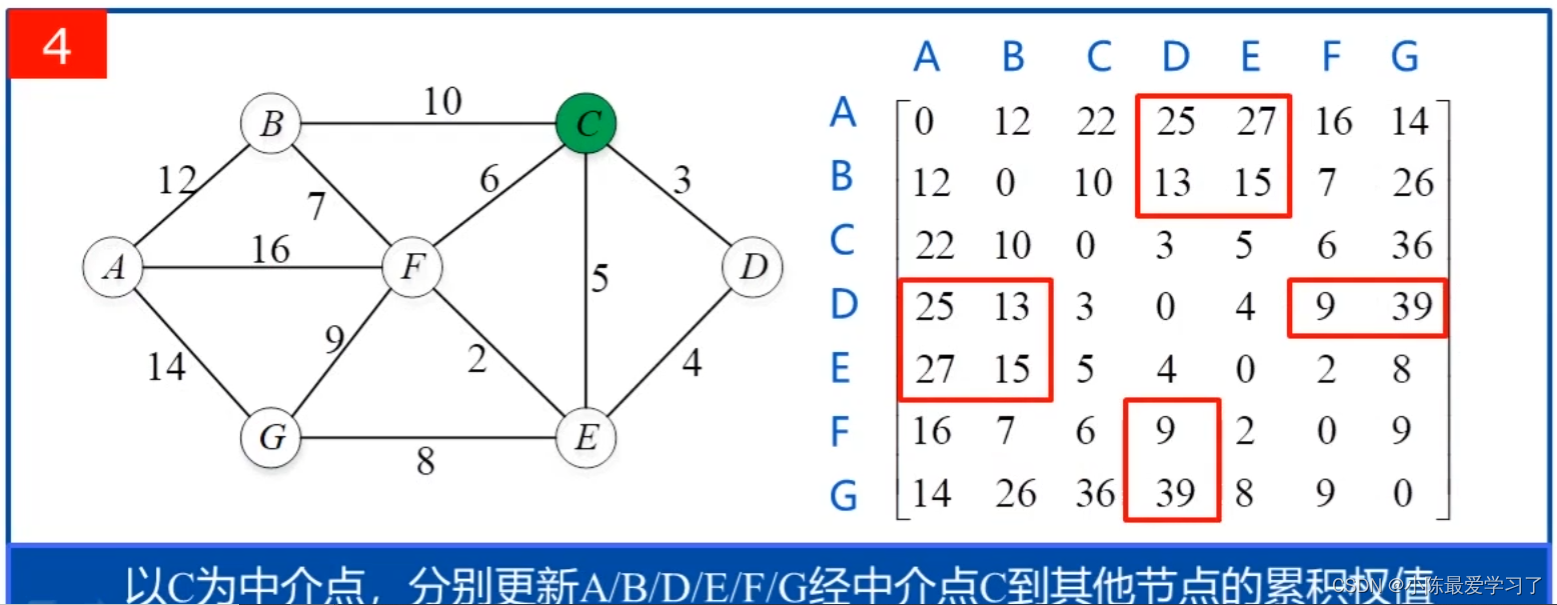
5.不断循环,直到以G为中介点更新彼此距离,最终得到以下矩阵:
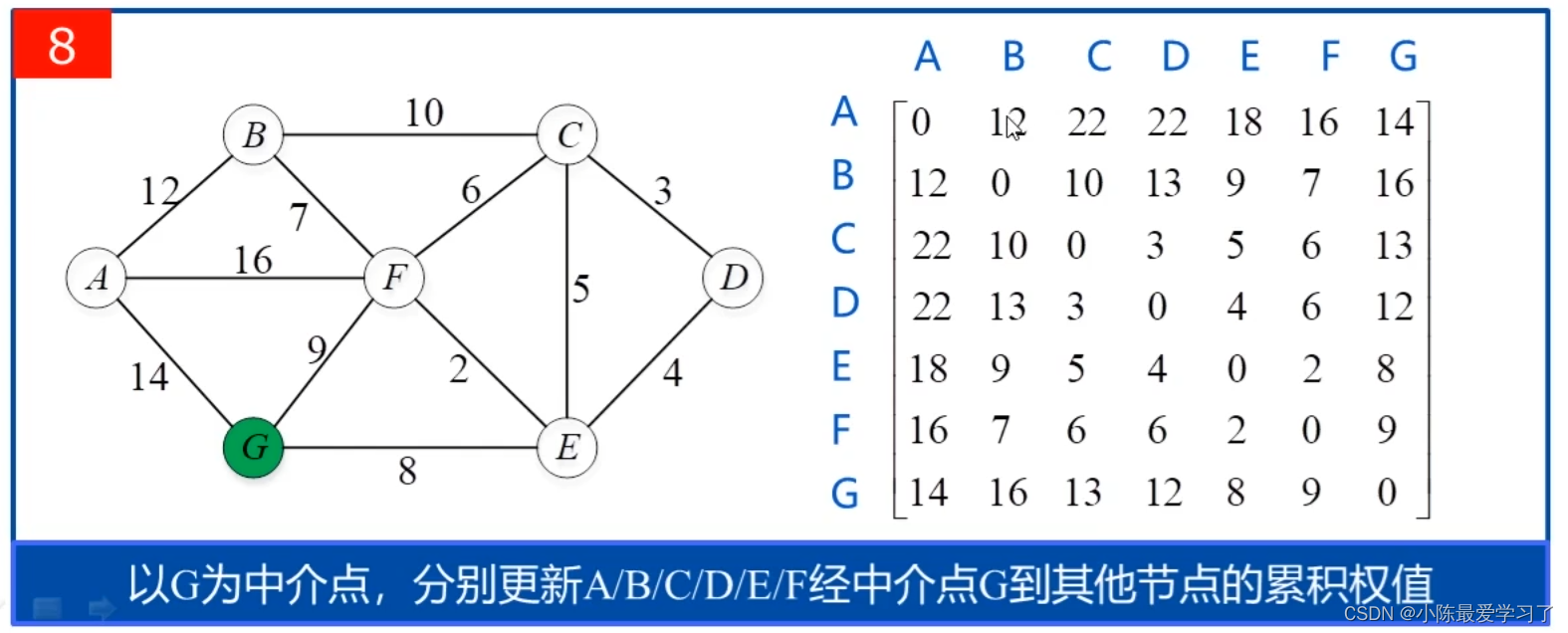
通过该图,我们可以读取任一两点之间的最短距离,如BC最小距离为10,FG为9,很直观,但是具有比较高的时间复杂度,第一层循环为选取中介点有n个节点,第二层循环有n-1个节点,计算与除开第一第二层所选取的两个节点外的n-2个节点的距离,故为O(n3)。
二Floyd*算法核心代码*(原理比较简单,直接用MATLAB仿真了):
已经上传到github上了,注释很详细
GitHub - Adamaser/Path-Planning





![每日一题 --- 数组中的第 K 个最大元素[力扣][Go]](https://img-blog.csdnimg.cn/direct/0aa903ec391b40d59a7f981cfc7d0252.png)