目录
- 采药(01背包)
- 代码实现
- 装箱问题(01背包)
- 代码实现
- *宠物小精灵之收服(二维费用01背包)
- 题目分析
- 代码实现
- 数字组合(01背包)
- 代码实现
- 买书(完全背包)
- 代码实现
- 货币系统(完全背包)
- 代码实现
- 货币系统(完全背包)
- 思路
- 代码实现
- *多重背包问题 III(多重背包单调队列优化)
- 多重背包的三种解法
- 代码实现
- 庆功会(多重背包)
- 二进制优化实现
- 单调队列优化实现
- 混合背包问题(混合背包)
- 继承前次动态规划结果再计算
- 将完全背包转化为多重背包计算
- 二维费用的背包问题(二维费用01背包)
- 代码实现
- *潜水员(不少于&最小价值)
- 问题分析
- 代码实现
- *机器分配(分组背包 + 路径回溯)
- 问题分析
- 代码实现
- 开心的金明(01背包)
- 代码实现
- *有依赖的背包问题(树形DP)
- 状态表示
- 代码实现
- 选课(树形DP)
- 代码实现
- 背包问题求方案数(求最优方案总数)
- 代码实现
- 背包容量不超过思路的解法
- 背包容量恰好思路的解法
- *背包问题求具体方案(路径输出)
- 确保字典序最小输出路径
- 代码实现
- 能量石(贪心 + 恰好 + 01背包)
- 题目分析
- 代码实现
- 金明的预算方案(分组 + 二进制枚举)
- 代码实现
采药(01背包)
题目描述:
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。
为此,他想拜附近最有威望的医师为师。
医师为了判断他的资质,给他出了一个难题。
医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式:
输入文件的第一行有两个整数 T T T 和 M M M,用一个空格隔开, T T T 代表总共能够用来采药的时间, M M M 代表山洞里的草药的数目。
接下来的 M M M 行每行包括两个在 1 1 1 到 100 100 100 之间(包括 1 1 1 和 100 100 100)的整数,分别表示采摘某株草药的时间 和 这株草药的价值。
输出格式:
输出文件包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
数据范围:
1 ≤ T ≤ 1000 , 1 ≤ M ≤ 100 1 ≤ T ≤ 1000, 1 ≤ M ≤ 100 1≤T≤1000,1≤M≤100
输入样例:
70 3
71 100
69 1
1 2
输出样例:
3
代码实现
标准的01背包
import sys
input = sys.stdin.readlinet, m = map(int, input().strip().split())
nums = [list(map(int, input().strip().split())) for _ in range(m)]f = [0] * (t + 1)for i in range(m):for j in range(t, nums[i][0] - 1, -1):f[j] = max(f[j], f[j - nums[i][0]] + nums[i][1])print(f[-1])
装箱问题(01背包)
题目描述:
有一个箱子容量为 V V V,同时有 n n n 个物品,每个物品有一个体积(正整数)。
要求 n n n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入格式:
第一行是一个整数 V V V,表示箱子容量。
第二行是一个整数 n n n,表示物品数。
接下来 n n n 行,每行一个正整数(不超过 10000 10000 10000),分别表示这 n n n 个物品的各自体积。
输出格式:
一个整数,表示箱子剩余空间。
数据范围:
0 < V ≤ 20000 , 0 < n ≤ 30 0 < V ≤ 20000, 0 < n ≤ 30 0<V≤20000,0<n≤30
输入样例:
24
6
8
3
12
7
9
7
输出样例:
0
代码实现
将容量当成权值来进行计算
import sys
input = sys.stdin.readlinev = int(input().strip())
n = int(input().strip())w = [int(input().strip()) for _ in range(n)]f = [0] * (v + 1)for i in range(n):for j in range(v, w[i] - 1, -1):f[j] = max(f[j], f[j - w[i]] + w[i])print(v - f[-1])
*宠物小精灵之收服(二维费用01背包)
题目描述:
宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。
一天,小智和皮卡丘来到了小精灵狩猎场,里面有很多珍贵的野生宠物小精灵。
小智也想收服其中的一些小精灵。
然而,野生的小精灵并不那么容易被收服。
对于每一个野生小精灵而言,小智可能需要使用很多个精灵球才能收服它,而在收服过程中,野生小精灵也会对皮卡丘造成一定的伤害(从而减少皮卡丘的体力)。
当皮卡丘的体力小于等于 0 0 0 时,小智就必须结束狩猎(因为他需要给皮卡丘疗伤),而 使得皮卡丘体力小于等于 0 0 0 的野生小精灵也不会被小智收服。
当小智的精灵球用完时,狩猎也宣告结束。
我们假设小智遇到野生小精灵时有两个选择:收服它,或者离开它。
如果小智选择了收服,那么一定会扔出能够收服该小精灵的精灵球,而皮卡丘也一定会受到相应的伤害;如果选择离开它,那么小智不会损失精灵球,皮卡丘也不会损失体力。
小智的目标有两个:主要目标是收服尽可能多的野生小精灵;如果可以收服的小精灵数量一样,小智希望皮卡丘受到的伤害越小(剩余体力越大),因为他们还要继续冒险。
现在已知小智的精灵球数量和皮卡丘的初始体力,已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。
请问,小智该如何选择收服哪些小精灵以达到他的目标呢?
输入格式:
输入数据的第一行包含三个整数: N N N, M M M, K K K,分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。
之后的 K K K 行,每一行代表一个野生小精灵,包括两个整数:收服该小精灵需要的精灵球的数量,以及收服过程中对皮卡丘造成的伤害。
输出格式:
输出为一行,包含两个整数: C , R C , R C,R,分别表示最多收服 C C C 个小精灵,以及收服 C C C 个小精灵时皮卡丘的剩余体力值最多为 R R R。
数据范围:
0 < N ≤ 1000 , 0 < M ≤ 500 , 0 < K ≤ 100 0 < N ≤ 1000 ,0 < M ≤ 500 ,0 < K ≤ 100 0<N≤1000,0<M≤500,0<K≤100
输入样例1:
10 100 5
7 10
2 40
2 50
1 20
4 20
输出样例1:
3 30
输入样例2:
10 100 5
8 110
12 10
20 10
5 200
1 110
输出样例2:
0 100
题目分析
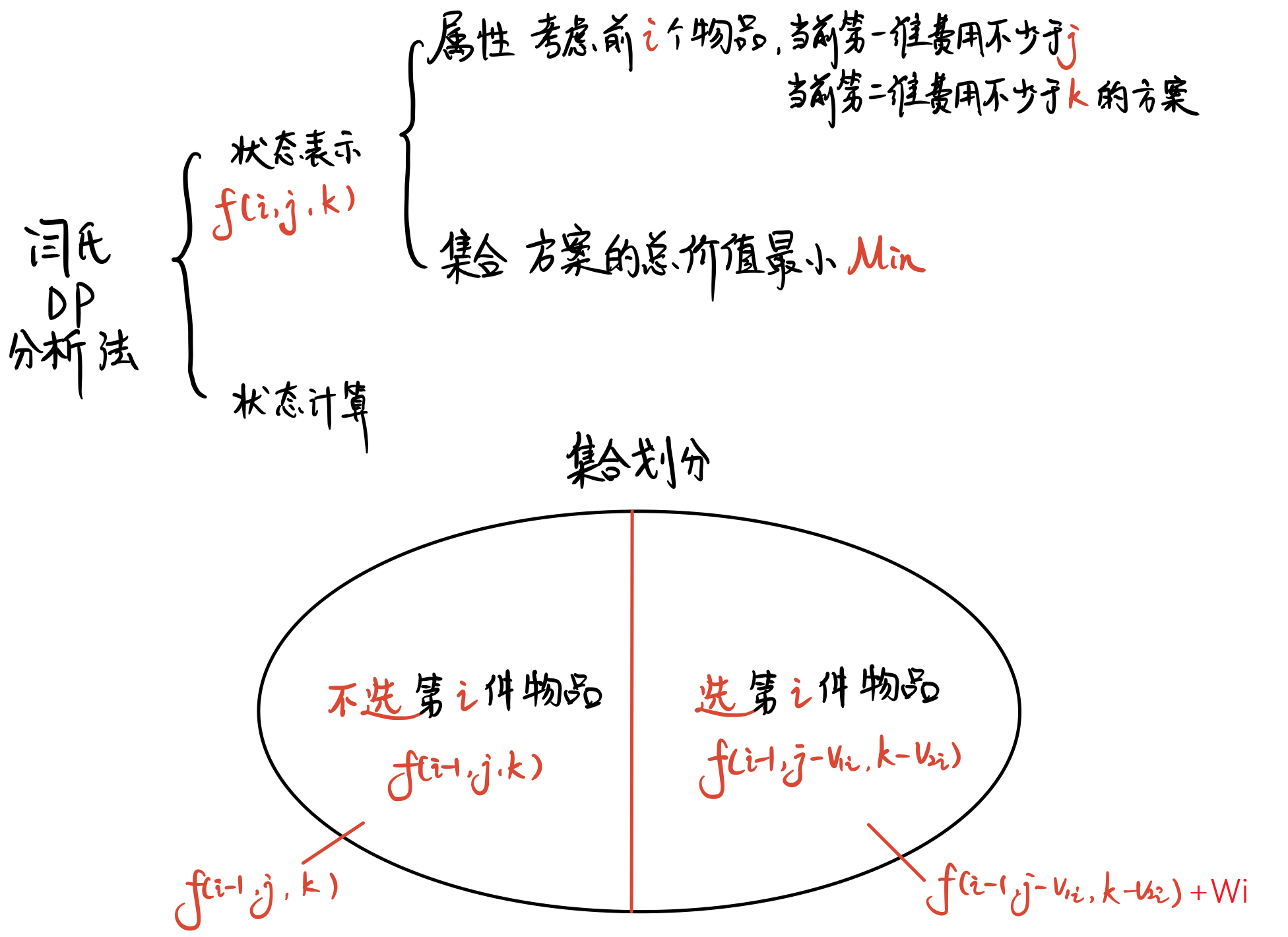
二维费用 01背包问题
把 野生的小精灵 看做物品,则捕捉他需要的 精灵球 个数就是第一费用,皮卡丘要掉的血就是 第二费用。
最后答案要求 物品数量 最多,因此我们可以用 状态的属性 来表示 选择的物品数。
代码实现
import sys
input = sys.stdin.readlinen, m, t = map(int, input().strip().split())
w = [tuple(map(int, input().strip().split())) for _ in range(t)]f = [[[0] * m for _ in range(n + 1)] for _ in range(t + 1)]for i in range(t):for j in range(n + 1):for k in range(m):f[i + 1][j][k] = f[i][j][k]if j >= w[i][0] and k >= w[i][1]:f[i + 1][j][k] = max(f[i][j - w[i][0]][k - w[i][1]] + 1, f[i + 1][j][k])for i in range(m):if f[-1][-1][i] == f[-1][-1][-1]:print(f[-1][-1][-1], m - i, end=' ')break
数字组合(01背包)
题目描述:
给定 N N N 个正整数 A 1 , A 2 , … , A N A_1, A_2, …, A_N A1,A2,…,AN,从中选出若干个数,使它们的和为 M M M,求有多少种选择方案。
输入格式:
第一行包含两个整数 N N N 和 M M M。
第二行包含 N N N 个整数,表示 A 1 , A 2 , … , A N A_1, A_2, …, A_N A1,A2,…,AN。
输出格式:
包含一个整数,表示可选方案数。
数据范围:
1 ≤ N ≤ 100 , 1 ≤ M ≤ 10000 , 1 ≤ A i ≤ 1000 1 ≤ N ≤ 100, 1 ≤ M ≤ 10000, 1 ≤ Ai ≤ 1000 1≤N≤100,1≤M≤10000,1≤Ai≤1000,答案保证在 i n t int int 范围内。
输入样例:
4 4
1 1 2 2
输出样例:
3
代码实现
01背包之恰好装完
import sys
from math import infinput = sys.stdin.readlinen, m = map(int, input().strip().split())
w = list(map(int, input().strip().split()))f = [1] + [0] * mfor i in range(n):for j in range(m, w[i] - 1, -1):f[j] += f[j - w[i]]print(f[-1])
买书(完全背包)
题目描述:
小明有 m m m 块钱,现有 10 10 10 元, 20 20 20 元, 50 50 50 元, 100 100 100 元的书。
每本书可以购买多次,求小明有多少种买书方案,使得花费恰好为 m m m 块钱。
输入格式:
一个整数 n n n,代表总共钱数。
输出格式:
一个整数,代表选择方案种数。
数据范围:
0 ≤ n ≤ 1000 0 ≤ n ≤ 1000 0≤n≤1000
输入样例1:
20
输出样例1:
2
输入样例2:
15
输出样例2:
0
输入样例3:
0
输出样例3:
1
代码实现
f ( i , j ) = f ( i − 1 , j ) + f ( i − 1 , j − v i ) + . . . + f ( i − 1 , j − s ⋅ v i ) ① f ( i , j − v i ) = f ( i − 1 , j − v i ) + . . . + f ( i − 1 , j − s ⋅ v i ) ② f(i,j)=f(i-1,j)+f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)①\\ f(i,j-v_i)= f(i-1,j-v_i)+...+f(i-1,j-s\cdot v_i)② f(i,j)=f(i−1,j)+f(i−1,j−vi)+...+f(i−1,j−s⋅vi)①f(i,j−vi)= f(i−1,j−vi)+...+f(i−1,j−s⋅vi)②
⇒ f ( i , j ) = f ( i − 1 , j ) + f ( i , j − v i ) ⇒ \large f(i,j)=f(i−1,j)+f(i,j−v_i) ⇒f(i,j)=f(i−1,j)+f(i,j−vi)
import sys
input = sys.stdin.readlinew = [10, 20, 50, 100]
n = len(w)
m = int(input().strip())f = [1] + [0] * mfor i in range(n):for j in range(w[i], m + 1):f[j] += f[j - w[i]]
print(f[-1])
货币系统(完全背包)
题目描述:
给你一个 n n n 种面值的货币系统,求组成面值为 m m m 的货币有多少种方案。
输入格式:
第一行,包含两个整数 n n n 和 m m m。
接下来 n n n 行,每行包含一个整数,表示一种货币的面值。
输出格式:
共一行,包含一个整数,表示方案数。
数据范围:
n ≤ 15 , m ≤ 3000 n ≤ 15, m ≤ 3000 n≤15,m≤3000
输入样例:
3 10
1
2
5
输出样例:
10
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
w = [int(input().strip()) for _ in range(n)]f = [1] + [0] * mfor i in range(n):for j in range(w[i], m + 1):f[j] += f[j - w[i]]print(f[-1])
货币系统(完全背包)
题目描述:
在网友的国度中共有 n n n 种不同面额的货币,第 i i i 种货币的面额为 a [ i ] a[i] a[i],你可以假设每一种货币都有无穷多张。
为了方便,我们把货币种数为 n n n、面额数组为 a [ 1.. n ] a[1..n] a[1..n] 的货币系统记作 ( n , a ) (n, a) (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x x x 都应该可以被表示出,即对每一个非负整数 x x x,都存在 n n n 个非负整数 t [ i ] t[i] t[i] 满足 a [ i ] × t [ i ] a[i] × t[i] a[i]×t[i] 的和为 x x x。
然而,在网友的国度中,货币系统可能是不完善的,即可能存在金额 x x x 不能被该货币系统表示出。
例如在货币系统 n = 3 , a = [ 2 , 5 , 9 ] n = 3, a = [2, 5, 9] n=3,a=[2,5,9] 中,金额 1 , 3 1, 3 1,3 就无法被表示出来。
两个货币系统 ( n , a ) (n, a) (n,a) 和 ( m , b ) (m, b) (m,b) 是等价的,当且仅当对于任意非负整数 x x x,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算 简化一下 货币系统。
他们希望找到一个货币系统 ( m , b ) (m, b) (m,b),满足 ( m , b ) (m, b) (m,b) 与原来的货币系统 ( n , a ) (n, a) (n,a) 等价,且 m m m 尽可能的小。
他们希望你来协助完成这个艰巨的任务:找到最小的 m m m。
输入格式:
输入文件的第一行包含一个整数 T T T,表示数据的组数。
接下来按照如下格式分别给出 T T T 组数据。
每组数据的第一行包含一个正整数 n n n。
接下来一行包含 n n n 个由空格隔开的正整数 a [ i ] a[i] a[i]。
输出格式:
输出文件共有 T T T 行,对于每组数据,输出一行一个正整数,表示所有与 ( n , a ) (n, a) (n,a) 等价的货币系统 ( m , b ) (m, b) (m,b) 中,最小的 m m m。
数据范围:
1 ≤ n ≤ 100 , 1 ≤ a [ i ] ≤ 25000 , 1 ≤ T ≤ 20 1 ≤ n ≤ 100, 1 ≤ a[i] ≤ 25000, 1 ≤ T ≤ 20 1≤n≤100,1≤a[i]≤25000,1≤T≤20
输入样例:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例:
2
5
思路
要求等价的货币系统 ( m , b ) (m, b) (m,b) 中,最小的 m m m,可以从 ( n , a ) (n, a) (n,a) 开始将不止被唯一构成的面额剔除,保留只能被本身构成一次的面额,就可以得到最小的m。
通过完全背包模型,把 0 ~ max(a) 的面额方案都求出来。然后根据已有面额依次遍历最终的每个面额的方案数,若 面额方案数 > 1 则代表这个面额表达方式不唯一,代表有其他方式可以构成该面额,即可以剔除,最终结果即为答案。
代码实现
import sys
input = sys.stdin.readlinet = int(input().strip())
for _ in range(t):n = int(input().strip())nums = list(map(int, input().strip().split()))m = max(nums)f = [1] + [0] * mfor i in range(n):for j in range(nums[i], m + 1):f[j] += f[j - nums[i]]ans = nfor i in range(n):if f[nums[i]] > 1:ans -= 1print(ans)
*多重背包问题 III(多重背包单调队列优化)
题目描述:
有 N N N 种物品和一个容量是 V V V 的背包。
第 i i i 种物品最多有 s i s_i si 件,每件体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。
输入格式:
第一行两个整数, N N N, V ( 0 < N ≤ 1000 , 0 < V ≤ 20000 ) V (0 < N ≤ 1000, 0 < V ≤ 20000) V(0<N≤1000,0<V≤20000),用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行三个整数 v i , w i , s i v_i, w_i, s_i vi,wi,si,用空格隔开,分别表示第 i i i 种物品的体积、价值和数量。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N ≤ 1000 0 < N ≤ 1000 0<N≤1000
0 < V ≤ 20000 0 < V ≤ 20000 0<V≤20000
0 < v i , w i , s i ≤ 20000 0 < v_i, w_i, s_i ≤ 20000 0<vi,wi,si≤20000
提示:
本题考查多重背包的单调队列优化方法。
输入样例:
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
多重背包的三种解法
| ①朴素版本 | ②二进制优化版本 | ③单调队列优化版本 |
|---|---|---|
| n ≤ 100 , V ≤ 100 n ≤ 100, V ≤ 100 n≤100,V≤100 | n ≤ 1000 , V ≤ 2000 n ≤ 1000, V ≤ 2000 n≤1000,V≤2000 | n ≤ 1000 , V ≤ 20000 n ≤ 1000, V ≤ 20000 n≤1000,V≤20000 |
单调队列优化视频
代码实现
import sys
from collections import dequeinput = sys.stdin.readline
n, m = map(int, input().strip().split())
f = [[0] * (m + 1) for _ in range(n + 1)]
q = deque()for i in range(n):v, w, s = map(int, input().strip().split()) # 体积、价值、数量for j in range(v):q.clear()for k in range(j, m + 1, v):if q and q[0] < k - v * s:q.popleft()while q and f[i][q[-1]] + (k - q[-1]) // v * w <= f[i][k]:q.pop()q.append(k)f[i + 1][k] = f[i][q[0]] + (k - q[0]) // v * wprint(f[-1][-1])
庆功会(多重背包)
题目描述:
为了庆贺班级在校运动会上取得全校第一名成绩,班主任决定开一场庆功会,为此拨款购买奖品犒劳运动员。
期望拨款金额能购买最大价值的奖品,可以补充他们的精力和体力。
输入格式:
第一行两个数 n n n, m m m,其中 n n n 代表希望购买的奖品的种数, m m m 表示拨款金额。
接下来 n n n 行,每行 3 3 3 个数 v 、 w 、 s v、w、s v、w、s,分别表示第 i i i 种奖品的价格、价值(价格与价值是不同的概念)和能购买的最大数量(买 0 0 0 件到 s s s 件均可)。
输出格式:
一行:一个数,表示此次购买能获得的最大的价值。
数据范围:
n ≤ 500 , m ≤ 6000 , v ≤ 100 , w ≤ 1000 , s ≤ 10 n ≤ 500, m ≤ 6000, v ≤ 100, w ≤ 1000, s ≤ 10 n≤500,m≤6000,v≤100,w≤1000,s≤10
输入样例:
5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1
输出样例:
1040
二进制优化实现
import sysinput = sys.stdin.readlinen, m = map(int, input().strip().split())
nums = []# 二进制优化
for _ in range(n):v, w, s = map(int, input().strip().split())t = 1while t <= s:nums.append((v * t, w * t))s -= tt *= 2if s > 0:nums.append((v * s, w * s))# 转化为01背包解决
n = len(nums)
f = [0] * (m + 1)for i in range(n):for j in range(m, nums[i][0] - 1, -1):f[j] = max(f[j], f[j - nums[i][0]] + nums[i][1])print(f[-1])
单调队列优化实现
import sys
from collections import deque
input = sys.stdin.readline# 单调队列做法
n, m = map(int, input().strip().split())
f = [[0] * (m + 1) for _ in range(n + 1)]
q = deque()for i in range(n):v, w, s = map(int, input().strip().split())for j in range(v):q.clear()for k in range(j, m + 1, v):if q and q[0] < k - s * v:q.popleft()while q and f[i][k] >= f[i][q[-1]] + (k - q[-1]) // v * w:q.pop()q.append(k)f[i + 1][k] = f[i][q[0]] + (k - q[0]) // v * wprint(f[-1][-1])
混合背包问题(混合背包)
题目描述:
有 n n n 种物品和一个容量为 m m m 的背包。
物品分三类:
-
第一类物品只能用 1 1 1 次(01背包)。
-
第二类物品可以用无限次(完全背包)。
-
第三类物品最多只能用 s i s_i si 次(多重背包)。
每种物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解一个选物品的方案,使得物品总体积不超过背包的容量,且总价值最大。
输入格式:
第一行两个整数, N , V N, V N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行三个整数 v i , w i , s i v_i, w_i, s_i vi,wi,si,用空格隔开,分别表示第 i i i 种物品的体积、价值和数量。
s i = − 1 si = -1 si=−1 表示第 i i i 种物品只能用 1 1 1 次;
s i = 0 si = 0 si=0 表示第 i i i 种物品可以用无限次;
s i > 0 si > 0 si>0 表示第 i i i 种物品可以使用 s i s_i si 次;
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N , V ≤ 1000 , 0 < v i , w i ≤ 1000 , − 1 ≤ s i ≤ 1000 0 < N, V ≤ 1000, 0 < v_i, w_i ≤ 1000, -1 ≤ s_i ≤ 1000 0<N,V≤1000,0<vi,wi≤1000,−1≤si≤1000
输入样例:
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出样例:
8
继承前次动态规划结果再计算
将01背包与二进制后的多重背包作为一类,记为 num1, 以01背包模型计算一次动态规划的结果,然后将完全背包单独作为一类,记为 num2, 以完全背包模型,在上回的动态规划的结果上,再计算一次动态规划的结果,便得到答案。
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
nums1 = []
nums2 = []for _ in range(n):v, w, s = map(int, input().strip().split())if s == 0:nums2.append((v, w))elif s == -1:nums1.append((v, w))else:t = 1while t <= s:nums1.append((v * t, w * t))s -= tt *= 2if s > 0:nums1.append((v * s, w * s))n1, n2 = len(nums1), len(nums2)
f = [0] * (m + 1)for i in range(n1):for j in range(m, nums1[i][0] - 1, -1):f[j] = max(f[j - nums1[i][0]] + nums1[i][1], f[j])for i in range(n2):for j in range(nums2[i][0], m + 1):f[j] = max(f[j], f[j - nums2[i][0]] + nums2[i][1])print(f[-1])
将完全背包转化为多重背包计算
import sys
input = sys.stdin.readline# 将完全背包转化为多重背包计算
n, m = map(int, input().strip().split())
nums = []for _ in range(n):v, w, s = map(int, input().strip().split())if s == -1:nums.append((v, w))else:if s == 0:s = m // vt = 1while t <= s:nums.append((v * t, w * t))s -= tt *= 2if s > 0:nums.append((v * s, w * s))n = len(nums)
f = [0] * (n + 1)
for i in range(n):for j in range(m, nums[i][0] - 1, -1):f[j] = max(f[j], f[j - nums[i][0]] + nums[i][1])print(f[-1])
二维费用的背包问题(二维费用01背包)
题目描述:
有 N N N 件物品和一个容量是 V V V 的背包,背包能承受的最大重量是 M M M。
每件物品只能用一次。体积是 v i v_i vi,重量是 m i m_i mi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
输入格式:
第一行三个整数, N , V , M N, V, M N,V,M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N N N 行,每行三个整数 v i , m i , w i v_i, m_i, w_i vi,mi,wi,用空格隔开,分别表示第 i i i 件物品的体积、重量和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围:
0 < N ≤ 1000 0 < N ≤ 1000 0<N≤1000
0 < V , M ≤ 100 0 < V, M ≤ 100 0<V,M≤100
0 < v i , m i ≤ 100 0 < v_i, m_i ≤ 100 0<vi,mi≤100
0 < w i ≤ 1000 0 < w_i ≤ 1000 0<wi≤1000
代码实现
import sys
input = sys.stdin.readlinen, m, t = map(int, input().strip().split())
f = [[0] * (t + 1) for _ in range(m + 1)]for i in range(n):v, s, w = map(int, input().strip().split())for j in range(m, v - 1, -1):for k in range(t, s - 1, -1):f[j][k] = max(f[j][k], f[j - v][k - s] + w)print(f[-1][-1])
*潜水员(不少于&最小价值)
题目描述:
潜水员为了潜水要使用特殊的装备。
他有一个带 2 2 2 种气体的气缸:一个为氧气,一个为氮气。
让潜水员下潜的深度需要各种数量的氧和氮。
潜水员有一定数量的气缸。
每个气缸都有重量和气体容量。
潜水员为了完成他的工作需要特定数量的氧和氮。
他完成工作所需气缸的总重的最低限度的是多少?
例如:潜水员有 5 5 5 个气缸。每行三个数字为:氧,氮的(升)量和气缸的重量:
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
如果潜水员需要 5 5 5 升的氧和 60 60 60 升的氮则总重最小为 249 249 249 ( 1 , 2 1,2 1,2或者 4 , 5 4,5 4,5号气缸)。
你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。
输入格式:
第一行有 2 2 2 个整数 m , n m,n m,n。它们表示氧,氮各自需要的量。
第二行为整数 k k k 表示气缸的个数。
此后的 k k k 行,每行包括 a i , b i , c i a_i,b_i,c_i ai,bi,ci, 3 3 3 个整数。这些各自是:第 i i i 个气缸里的氧和氮的容量及气缸重量。
输出格式:
仅一行包含一个整数,为潜水员完成工作所需的气缸的重量总和的最低值。
数据范围:
1 ≤ m ≤ 21 1 ≤ m ≤ 21 1≤m≤21
1 ≤ n ≤ 79 1 ≤ n ≤ 79 1≤n≤79
1 ≤ k ≤ 1000 1 ≤ k ≤ 1000 1≤k≤1000
1 ≤ a i ≤ 21 1 ≤ a_i ≤ 21 1≤ai≤21
1 ≤ b i ≤ 79 1 ≤ b_i ≤ 79 1≤bi≤79
1 ≤ c i ≤ 800 1 ≤ c_i ≤ 800 1≤ci≤800
输入样例:
5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
输出样例:
249
问题分析
本题是一个 二维费用01背包问题 ,但和一般的 二维费用01背包问题 不同这题要求的是 费用不少于 规定条件,因此我们需要对于 状态的定义进行改变。
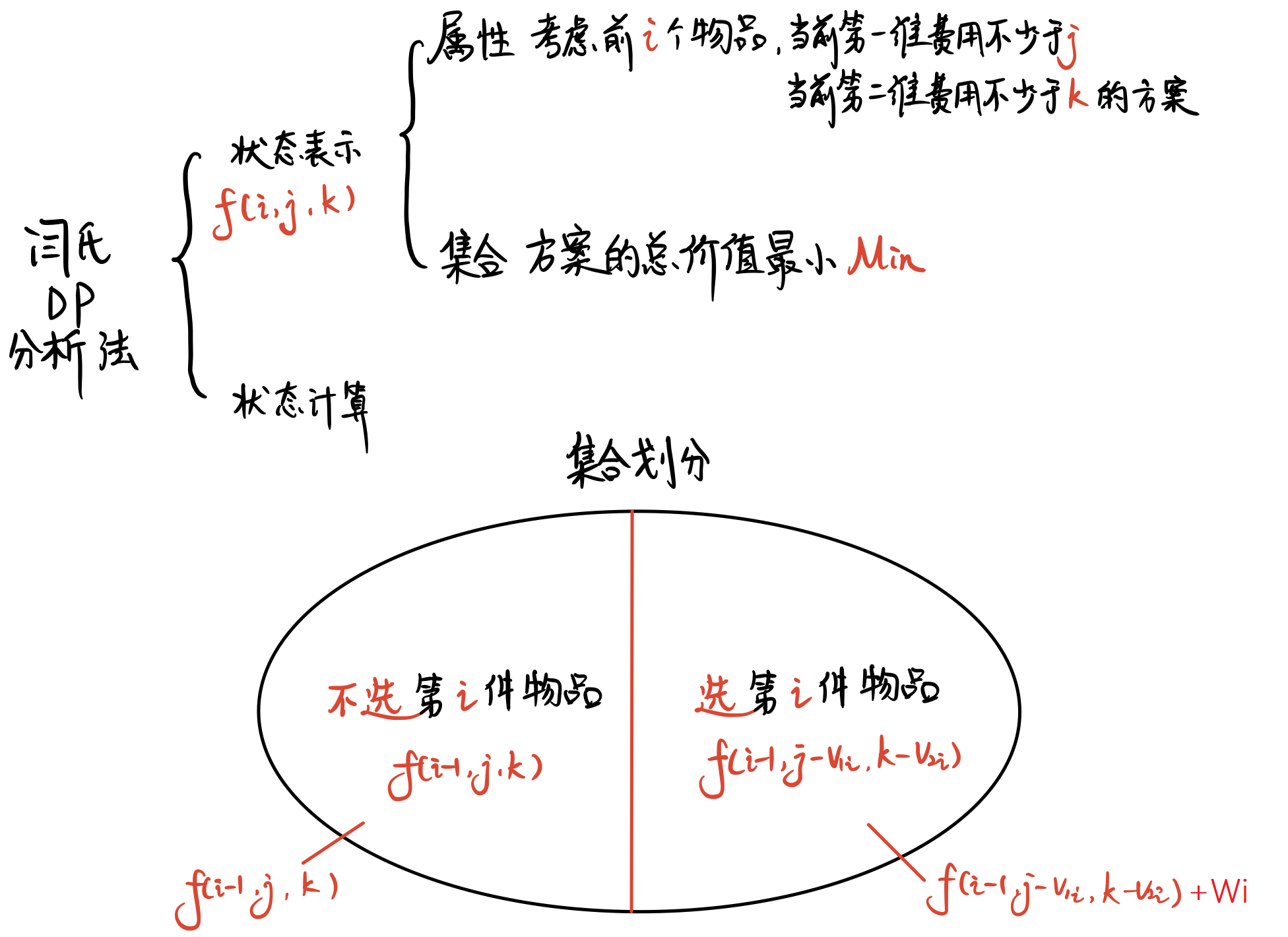
有普通的二维费用背包问题中, j , k j, k j,k 是不能进行超载的,超过了背包就太重, 背包就漏了!在本题中是 可以超载的。
考虑在枚举背包容量不足当前物品的容量时,也将当前物品装入背包(用f[max(0, i - v1)][max(0, j - v2)] + w) 来进行更新),这样枚举到最大容量的同时即可保证背包容量不出现小于目标的情况,也可以表示实际上超出容量的结果。妙!
代码实现
import sys
from math import inf
input = sys.stdin.readlinem, n = map(int, input().strip().split())
t = int(input().strip())
f = [[inf] * (n + 1) for _ in range(m + 1)]
f[0][0] = 0for i in range(t):a, b, c = map(int, input().strip().split())for j in range(m, -1, -1):for k in range(n, -1, -1):# max(j - a, 0) 与 max(k - b, 0) 使得枚举的背包容量可以表示实际上超出容量的结果f[j][k] = min(f[max(j - a, 0)][max(k - b, 0)] + c, f[j][k])print(f[-1][-1])
*机器分配(分组背包 + 路径回溯)
题目描述:
总公司拥有 M M M 台相同的高效设备,准备分给下属的 N N N 个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这 M M M 台设备才能使国家得到的盈利最大?
求出最大盈利值。
分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数 M M M。
输入格式:
第一行有两个数,第一个数是分公司数 N N N,第二个数是设备台数 M M M;
接下来是一个 N × M N×M N×M 的矩阵,矩阵中的第 i i i 行第 j j j 列的整数表示第 i i i 个公司分配 j j j 台机器时的盈利。
输出格式:
第一行输出最大盈利值;
接下 N N N 行,每行有 2 2 2 个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输出任意合法方案即可。
数据范围:
1 ≤ N ≤ 10 , 1 ≤ M ≤ 15 1 ≤ N ≤ 10, 1 ≤ M ≤ 15 1≤N≤10,1≤M≤15
输入样例:
3 3
30 40 50
20 30 50
20 25 30
输出样例:
70
1 1
2 1
3 1
最小字典序的数据:
输入样例:
2 15
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
输出样例:
2
1 0
2 15
问题分析
转化为分组背包问题
将 N N N 个公司看成 N N N 个组,把 M M M 看作背包的最大容量,每个组从得到 1 1 1 ~ M M M 的物品价值。
路径回溯(记录路径法)
for i in range(n):for j in range(m + 1):f[i + 1][j] = f[i][j]for k in range(1, j + 1):val = f[i][j - k] + nums[i][k - 1]if val >= f[i + 1][j]:f[i + 1][j] = valpath[i + 1][j] = k
- 如果 v a l > f [ i ] [ j ] val > f[i][j] val>f[i][j] 转移,打印出来的路径是字典序最大的。
- 如果 v a l ≥ f [ i ] [ j ] val ≥ f[i][j] val≥f[i][j] 转移,打印出来的路径是字典序最小的。
观察 f [ i ] [ j − k ] f[i][j-k] f[i][j−k],计算式是 j − k j - k j−k, k k k 前面的符号是负号,也就是 k k k 越小, j − k j - k j−k 越大; k k k 越大,值越小。按这个逻辑,随着 k k k 长大,就会枚举到更小的 j − k j - k j−k。
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
nums = [list(map(int, input().strip().split())) for _ in range(n)]f = [[0] * (m + 1) for _ in range(n + 1)]
path = [[0] * (m + 1) for _ in range(n + 1)]# 路径回溯
def get_path(x, y):if x == 0:returnget_path(x - 1, y - path[x][y])print(x, path[x][y], end=' ')print()for i in range(n):for j in range(m + 1):f[i + 1][j] = f[i][j]for k in range(1, j + 1):val = f[i][j - k] + nums[i][k - 1]if val >= f[i + 1][j]:f[i + 1][j] = valpath[i + 1][j] = kprint(f[-1][-1])
get_path(n, m)
开心的金明(01背包)
题目描述:
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 N N N 元钱就行”。
今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的 N N N 元。
于是,他把每件物品规定了一个重要度,分为 5 5 5 等:用整数 1 1 1 ~ 5 5 5 表示,第 5 5 5 等最重要。
他还从因特网上查到了每件物品的价格(都是整数元)。
他希望在不超过 N N N 元(可以等于 N N N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j j j 件物品的价格为 v [ j ] v[j] v[j],重要度为 w [ j ] w[j] w[j],共选中了 k k k 件物品,编号依次为 j 1 , j 2 , … , j k j_1, j_2, …, j_k j1,j2,…,jk,则所求的总和为:
v [ j 1 ] × w [ j 1 ] + v [ j 2 ] × w [ j 2 ] + … + v [ j k ] × w [ j k ] v[j_1]×w[j_1]+v[j_2]×w[j_2]+…+v[j_k]×w[j_k] v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]
请你帮助金明设计一个满足要求的购物单。
输入格式:
输入文件的第 1 1 1 行,为两个正整数 N N N 和 m m m,用一个空格隔开。(其中 N N N 表示总钱数, m m m 为希望购买物品的个数)
从第 2 2 2 行到第 m + 1 m+1 m+1 行,第 j j j 行给出了编号为 j − 1 j - 1 j−1 的物品的基本数据,每行有 2 2 2 个非负整数 v v v 和 p p p。(其中 v v v 表示该物品的价格, p p p 表示该物品的重要度)
输出格式:
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(数据保证结果不超过 1 0 8 10^8 108)。
数据范围:
1 ≤ N < 30000 , 1 ≤ m < 25 , 0 ≤ v ≤ 10000 , 1 ≤ p ≤ 5 1 ≤ N < 30000, 1 ≤ m < 25, 0 ≤ v ≤ 10000, 1 ≤ p ≤ 5 1≤N<30000,1≤m<25,0≤v≤10000,1≤p≤5
输入样例:
1000 5
800 2
400 5
300 5
400 3
200 2
输出样例:
3900
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
w = [tuple(map(int, input().strip().split())) for _ in range(m)]f = [0] * (n + 1)
for i in range(m):for j in range(n, w[i][0] - 1, -1):f[j] = max(f[j], f[j - w[i][0]] + w[i][0] * w[i][1])print(f[-1])
*有依赖的背包问题(树形DP)
题目描述:
有 N N N 个物品和一个容量是 V V V 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
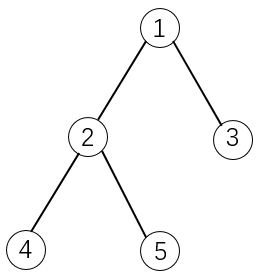
如果选择物品 5 5 5,则必须选择物品 1 1 1 和 2 2 2。这是因为 2 2 2 是 5 5 5 的父节点, 1 1 1 是 2 2 2 的父节点。
每件物品的编号是 i i i,体积是 v i v_i vi,价值是 w i w_i wi,依赖的父节点编号是 p i p_i pi。物品的下标范围是 1 … N 1…N 1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行有两个整数 N , V N, V N,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 N N N 行数据,每行数据表示一个物品。
第 i i i 行有三个整数 v i , w i , p i v_i, w_i, p_i vi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果 p i = − 1 p_i = -1 pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式:
输出一个整数,表示最大价值。
数据范围:
1 ≤ N , V ≤ 100 1 ≤ N, V ≤ 100 1≤N,V≤100
1 ≤ v i , w i ≤ 100 1 ≤ v_i, w_i ≤ 100 1≤vi,wi≤100
父节点编号范围:
-
内部结点: 1 ≤ p i ≤ N 1 ≤ p_i ≤ N 1≤pi≤N
-
根节点 : p i = − 1 p_i = -1 pi=−1
输入样例:
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例:
11
状态表示
枚举每个 状态 分给各个子节点 的 体积
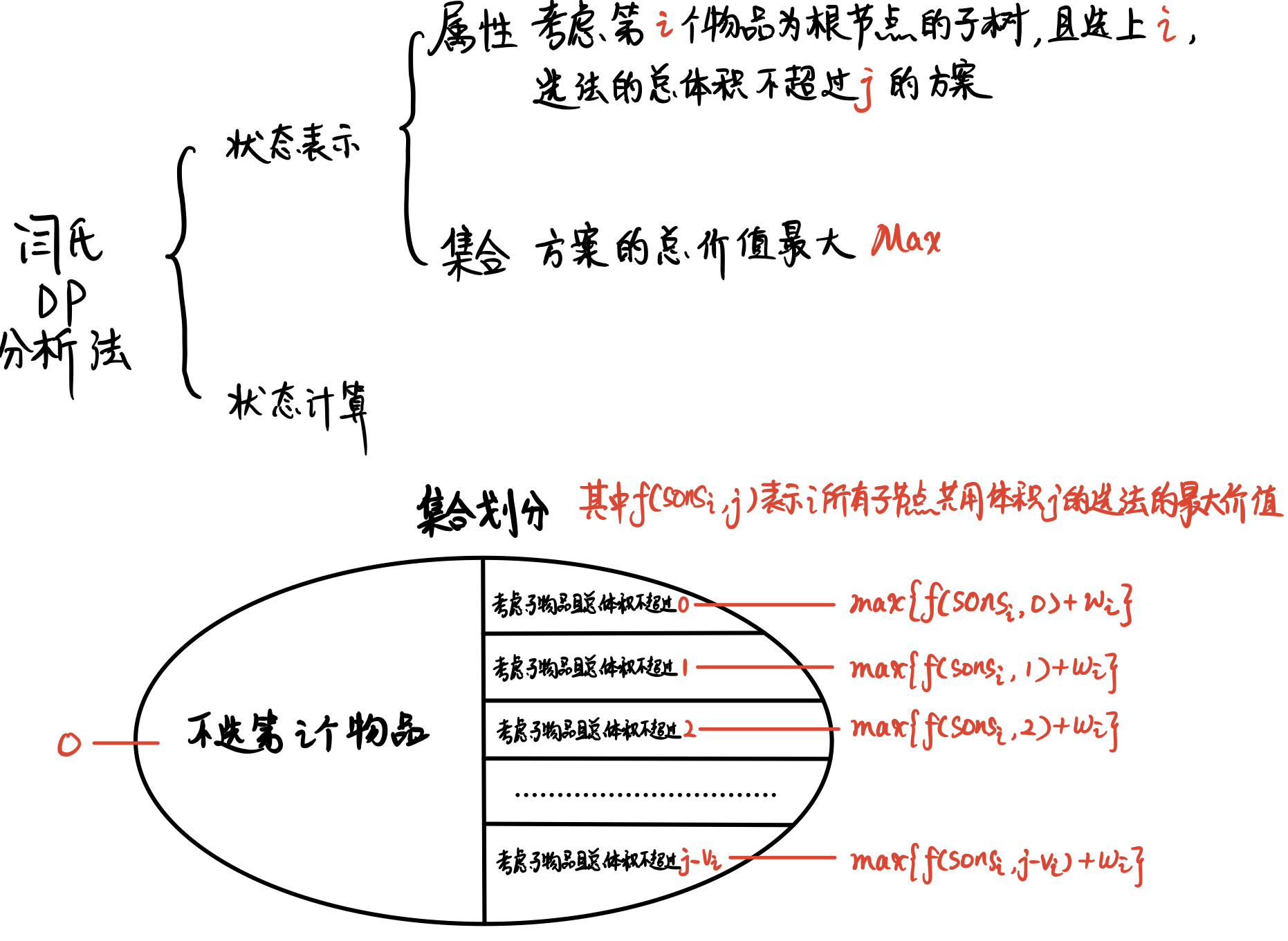
采用倒序遍历 防止一个节点被同一子节点多次更新
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
nums = [(0, 0) for _ in range(n)]
g = [[] for _ in range(n)]
root = 0for i in range(n):v, w, p = map(int, input().strip().split())nums[i] = (v, w)if p == -1:root = ielse:g[p - 1].append(i)f = [[0] * (m + 1) for _ in range(n)]def dfs(x):for y in g[x]:dfs(y)# 类似分组背包的更新模式# 采用倒序遍历 防止一个节点被同一子节点多次更新# 枚举所有要被更新的状态for j in range(m - nums[x][0], -1, -1):# 枚举该子节点在体积j下能使用的所有可能体积数for k in range(j + 1):f[x][j] = max(f[x][j], f[x][j - k] + f[y][k])# 选取for j in range(m, nums[x][0] - 1, -1):f[x][j] = f[x][j - nums[x][0]] + nums[x][1]# 未选取(清零)for j in range(nums[x][0]):f[x][j] = 0dfs(root)
print(f[root][-1])
选课(树形DP)
题目描述:
学校实行学分制。
每门的必修课都有固定的学分,同时还必须获得相应的选修课程学分。
学校开设了 N N N 门的选修课程,每个学生可选课程的数量 M M M 是给定的。
学生选修了这 M M M 门课并考核通过就能获得相应的学分。
在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其他的一些课程的基础上才能选修。
例如《Windows程序设计》必须在选修了《Windows操作基础》之后才能选修。
我们称《Windows操作基础》是《Windows程序设计》的先修课。
每门课的直接先修课最多只有一门。
两门课可能存在相同的先修课。
你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修条件。
假定课程之间不存在时间上的冲突。
输入格式:
输入文件的第一行包括两个整数 N 、 M N、M N、M(中间用一个空格隔开)其中 1 ≤ N ≤ 300 , 1 ≤ M ≤ N 1≤N≤300,1≤M≤N 1≤N≤300,1≤M≤N。
接下来 N 行每行代表一门课,课号依次为 1 , 2 , … , N 1,2,…,N 1,2,…,N。
每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为 0 0 0),第二个数为这门课的学分。
学分是不超过 10 10 10 的正整数。
输出格式:
输出一个整数,表示学分总数。
输入样例:
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
输出样例:
13
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())
g = [[] for _ in range(n + 1)]
nums = [0 for _ in range(n + 1)]for i in range(1, n + 1):fa, w = map(int, input().strip().split())g[fa].append(i)nums[i] = w# 由于把 0 虚拟节点算入,所以容量应再扩大
m += 1
f = [[0] * (m + 1) for _ in range(n + 1)]def dfs(x):for y in g[x]:dfs(y)for j in range(m - 1, -1, -1):for k in range(j + 1):f[x][j] = max(f[x][j], f[x][j - k] + f[y][k])for j in range(m, 0, -1):f[x][j] = f[x][j - 1] + nums[x]dfs(0)
print(f[0][-1])背包问题求方案数(求最优方案总数)
题目描述:
有 N N N 件物品和一个容量是 V V V 的背包。每件物品只能使用一次。
第 i i i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最优选法的方案数。注意答案可能很大,请输出答案模 1 0 9 + 7 10^9 + 7 109+7 的结果。
输入格式:
第一行两个整数 N , V N,V N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i, w_i vi,wi,用空格隔开,分别表示第 i i i 件物品的体积和价值。
输出格式:
输出一个整数,表示 方案数 模 1 0 9 + 7 10^9 + 7 109+7 的结果。
数据范围:
0 < N , V ≤ 1000 0 < N, V ≤ 1000 0<N,V≤1000
0 < v i , w i ≤ 1000 0 < v_i, w_i ≤ 1000 0<vi,wi≤1000
输入样例:
4 5
1 2
2 4
3 4
4 6
输出样例:
2
代码实现
背包容量不超过思路的解法
import sys
input = sys.stdin.readlineMOD = 10 ** 9 + 7n, m = map(int, input().strip().split())
f, g = [0] * (m + 1), [1] * (m + 1)for i in range(n):v, w = map(int, input().strip().split())for j in range(m, v - 1, -1):if f[j] < f[j - v] + w:f[j] = f[j - v] + wg[j] = g[j - v]elif f[j] == f[j - v] + w:g[j] = (g[j] + g[j - v]) % MODprint(g[-1])
背包容量恰好思路的解法
由于定义的状态表示是空间恰好是 i i i,那么最大值的产生,可不一定存储在空间恰好是 m m m 的状态下, m m m及以下的各个状态,都可能装着最大值。
f, g = [0] + [-inf] * m, [1] + [0] * mfor i in range(n):v, w = map(int, input().strip().split())for j in range(m, v - 1, -1):if f[j] < f[j - v] + w:f[j] = f[j - v] + wg[j] = g[j - v]elif f[j] == f[j - v] + w:g[j] = (g[j] + g[j - v]) % MOD# 得到各种空间容量下的最大价值
max_val = max(f)# 添加等于最大价值的方案
ans = sum(g[i] for i in range(m + 1) if max_val == f[i])print(ans)
*背包问题求具体方案(路径输出)
题目描述:
有 N N N 件物品和一个容量是 V V V 的背包。每件物品只能使用一次。
第 i i i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1 … N 1…N 1…N。
输入格式:
第一行两个整数 N , V N,V N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i, w_i vi,wi,用空格隔开,分别表示第 i i i 件物品的体积和价值。
输出格式:
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1 … N 1…N 1…N。
数据范围:
0 < N , V ≤ 1000 0 < N, V ≤ 1000 0<N,V≤1000
0 < v i , w i ≤ 1000 0 < v_i, w_i ≤ 1000 0<vi,wi≤1000
输入样例:
4 5
1 2
2 4
3 4
4 6
输出样例:
1 4
确保字典序最小输出路径
由于是从 0 0 0 到 n − 1 n - 1 n−1 件物品的枚举,所以最后状态的结果是 f [ n ] [ m ] f[n][m] f[n][m]。路径回溯便是从 n − 1 n - 1 n−1 回溯至 0 0 0,从而得到选择的物品,但是由于从后往前的顺序关系,较大序号的物品的更新状态会被优先考虑。比如:状态 f [ 10 ] [ 50 ] f[10][50] f[10][50] 可以分别由 f [ 5 ] [ 20 ] ⇒ f [ 10 ] [ 50 ] f[5][20]⇒ f[10][50] f[5][20]⇒f[10][50] 和 f [ 9 ] [ 30 ] ⇒ f [ 10 ] [ 50 ] f[9][30]⇒ f[10][50] f[9][30]⇒f[10][50] 回溯会优先更新为 [ 9 ] [ 30 ] [9][30] [9][30],从而导致字典序最大。
要求字典序最小输出,即反过来枚举物品,从 n − 1 n - 1 n−1 到 0 0 0 件物品,由此最后状态的结果是 f [ 0 ] [ m ] f[0][m] f[0][m]。再后回溯路径便从 0 0 0 到 n − 1 n - 1 n−1 件物品,开始找选择的物品,此时字典序最小。
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())f = [[0] * (m + 1) for _ in range(n + 1)]w = [tuple(map(int, input().strip().split())) for _ in range(n)]for i in range(n - 1, -1, -1):for j in range(m + 1):f[i][j] = f[i + 1][j]if j >= w[i][0] and f[i + 1][j - w[i][0]] + w[i][1] > f[i][j]:f[i][j] = f[i + 1][j - w[i][0]] + w[i][1]# 路径回溯
j = m
for i in range(n):if j >= w[i][0] and f[i][j] == f[i + 1][j - w[i][0]] + w[i][1]:j -= w[i][0]print(i + 1, end=' ')
能量石(贪心 + 恰好 + 01背包)
题目描述:
岩石怪物杜达生活在魔法森林中,他在午餐时收集了 N N N 块能量石准备开吃。
由于他的嘴很小,所以一次只能吃一块能量石。
能量石很硬,吃完需要花不少时间。
吃完第 i i i 块能量石需要花费的时间为 S i S_i Si 秒。
杜达靠吃能量石来获取能量。
不同的能量石包含的能量可能不同。
此外,能量石会随着时间流逝逐渐失去能量。
第 i i i 块能量石最初包含 E i E_i Ei 单位的能量,并且每秒将失去 L i L_i Li 单位的能量。
当杜达开始吃一块能量石时,他就会立即获得该能量石所含的全部能量(无论实际吃完该石头需要多少时间)。
能量石中包含的能量最多降低至 0 0 0。
请问杜达通过吃能量石可以获得的最大能量是多少?
输入格式:
第一行包含整数 T T T,表示共有 T T T 组测试数据。
每组数据第一行包含整数 N N N,表示能量石的数量。
接下来 N N N 行,每行包含三个整数 S i , E i , L i S_i, E_i, L_i Si,Ei,Li。
输出格式:
每组数据输出一个结果,每个结果占一行。
结果表示为 Case #x: y,其中 x 是组别编号(从 1 1 1 开始),y 是可以获得的最大能量值。
数据范围:
1 ≤ T ≤ 10 1 ≤ T ≤ 10 1≤T≤10
1 ≤ N ≤ 100 1 ≤ N ≤ 100 1≤N≤100
1 ≤ S i ≤ 100 1 ≤ S_i ≤ 100 1≤Si≤100
1 ≤ E i ≤ 1 0 5 1 ≤ E_i ≤ 10^5 1≤Ei≤105
0 ≤ L i ≤ 1 0 5 0 ≤ L_i ≤ 10^5 0≤Li≤105
输入样例:
3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0
输出样例:
Case #1: 105
Case #2: 8
Case #3: 500
题目分析
推公式
经典的推公式类型的贪心。
a n s 1 = E 1 + E 2 − S 1 ∗ L 2 {ans}_1 = E_1 + E_2 - S_1 * L_2 ans1=E1+E2−S1∗L2
a n s 2 = E 1 + E 2 − S 2 ∗ L 1 {ans}_2 = E_1 + E_2 - S_2 * L_1 ans2=E1+E2−S2∗L1
让 a n s 1 ≤ a n s 2 {ans}_1 ≤ {ans}_2 ans1≤ans2 ,可以得到 S 2 ∗ L 1 ≤ S 1 ∗ L 2 S_2 * L_1 ≤ S_1 * L_2 S2∗L1≤S1∗L2, 即 L 1 S 1 ≤ L 2 S 2 \frac{L_1}{S_1} ≤ \frac{L_2}{S_2} S1L1≤S2L2,可以得到贪心公式结果,选择 L i S i \frac{L_i}{S_i} SiLi 越大的越是最优解。从而开始01背包做法,枚举当前时间作为容量,考虑恰好容量做法,通过排序优先选择 L i S i \frac{L_i}{S_i} SiLi 大的物品。
代码实现
import sys
from math import inf
input = sys.stdin.readlinet = int(input().strip())for q in range(1, t + 1):n = int(input().strip())# 排序为最优选取方案nums = sorted([tuple(map(int, input().strip().split())) for _ in range(n)], key=lambda x: x[2] // x[0], reverse=True)m = sum(nums[i][0] for i in range(n))f = [0] + [-inf] * mfor i in range(n):for j in range(m, nums[i][0] - 1, -1):f[j] = max(f[j], f[j - nums[i][0]] + max(nums[i][1] - (j - nums[i][0]) * nums[i][2], 0))print("Case #%d: %d\n" % (q, max(f)))
金明的预算方案(分组 + 二进制枚举)
题目描述:
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 N N N 元钱就行”。
今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
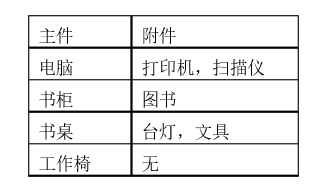
如果要买归类为附件的物品,必须先买该附件所属的主件。
每个主件可以有 0 0 0 个、 1 1 1 个或 2 2 2 个附件。
附件不再有从属于自己的附件。
金明想买的东西很多,肯定会超过妈妈限定的 N N N 元。
于是,他把每件物品规定了一个重要度,分为 5 5 5 等:用整数 1 1 1 ∼ 5 5 5 表示,第 5 5 5 等最重要。
他还从因特网上查到了每件物品的价格(都是 10 10 10 元的整数倍)。
他希望在不超过 N N N 元(可以等于 N N N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j j j 件物品的价格为 v [ j ] v[j] v[j],重要度为 w [ j ] w[j] w[j] ,共选中了 k k k 件物品,编号依次为 j 1 j_1 j1, j 2 j_2 j2,…, j k j_k jk,则所求的总和为:
v [ j 1 ] ∗ w [ j 1 ] + v [ j 2 ] ∗ w [ j 2 ] + … + v [ j k ] ∗ w [ j k ] v[j_1] * w[j_1] + v[j_2] * w[j_2] + … + v[j_k] * w[j_k] v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk](其中 ∗ * ∗ 为乘号)
请你帮助金明设计一个满足要求的购物单。
输入格式:
输入文件的第 1 1 1 行,为两个正整数,用一个空格隔开: N N N m m m,其中 N N N 表示总钱数, m m m 为希望购买物品的个数。
从第 2 2 2 行到第 m + 1 m+1 m+1 行,第 j 行给出了编号为 j − 1 j−1 j−1 的物品的基本数据,每行有 3 3 3 个非负整数 v p q,其中 v v v 表示该物品的价格, p p p 表示该物品的重要度( 1 1 1 ~ 5 5 5), q q q 表示该物品是主件还是附件。
如果 q = 0 q = 0 q=0,表示该物品为主件,如果 q > 0 q > 0 q>0,表示该物品为附件, q q q 是所属主件的编号。
输出格式:
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值( < 200000 < 200000 <200000)。
数据范围:
N < 32000 , m < 60 , v < 10000 N < 32000, m < 60, v < 10000 N<32000,m<60,v<10000
输入样例:
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出样例:
2200
代码实现
import sys
input = sys.stdin.readlinen, m = map(int, input().strip().split())a = [[] for _ in range(m)] # 主件
b = [[] for _ in range(m)] # 附件for i in range(m):w, p, q = map(int, input().strip().split())if not q:a[i].append((w, p * w))else:b[q - 1].append((w, p * w))for i in range(m):if not a[i]:continue# 利用二进制模拟所有 主件 + 附件 的选取情况for j in range(1, 1 << len(b[i])):sv, sw = a[i][0]for k in range(len(b)):if j >> k & 1:sv += b[i][k][0]sw += b[i][k][1]a[i].append((sv, sw)) # 将各种选取情况加入数组a中f = [0] * (n + 1)# 标准分组背包解决
for i in range(m):for j in range(n, -1, -1):for k in range(len(a[i])):if j >= a[i][k][0]:f[j] = max(f[j], f[j - a[i][k][0]] + a[i][k][1])print(f[-1])