01背包

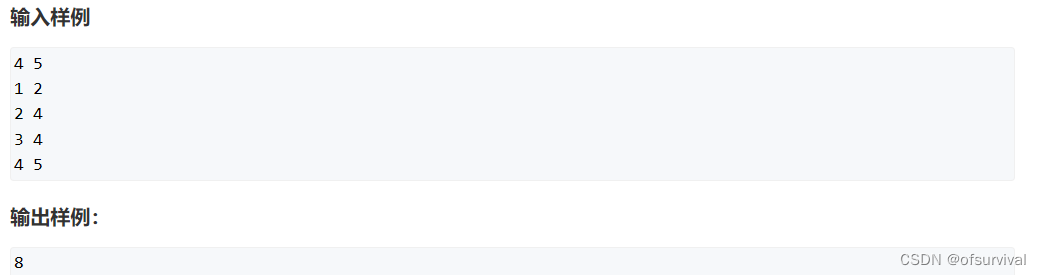
易知状态转移方程为:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])
代码
N,V = map(int,input().split())
v, w = [0],[0] # 体积v,价值w
for i in range(N):a = list(map(int,input().split()))v.append(a[0]) # 体积viw.append(a[1]) # 价值wi
dp = [[0 for j in range(V+1)] for i in range(N+1)] # 创建二维列表并初始化为0,行为物品数量,列为背包容量for i in range(1,N+1): # 物品数从0到Nfor j in range(1,V+1): # 背包容量从0到Vdp[i][j]=dp[i-1][j] # 先不选if j>=v[i]: # 当背包容量大于某个物品体积时选择价值大的那个dp[i][j] = max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])
print(dp[-1][-1])
从状态转移方程看,可以将二维数组dp优化为一维,每次更新第i行的状态值
代码
N,V = map(int,input().split())
v, w = [0],[0] # 体积v,价值w
for i in range(N):a = list(map(int,input().split()))v.append(a[0]) # 体积viw.append(a[1]) # 价值widp =[0 for i in range(V+1)] # 创建一维列表并初始化为0for i in range(1,N+1):for j in range(V,v[i]-1,-1):dp[j]= max(dp[j],dp[j-v[i]]+w[i])
print(dp[-1])