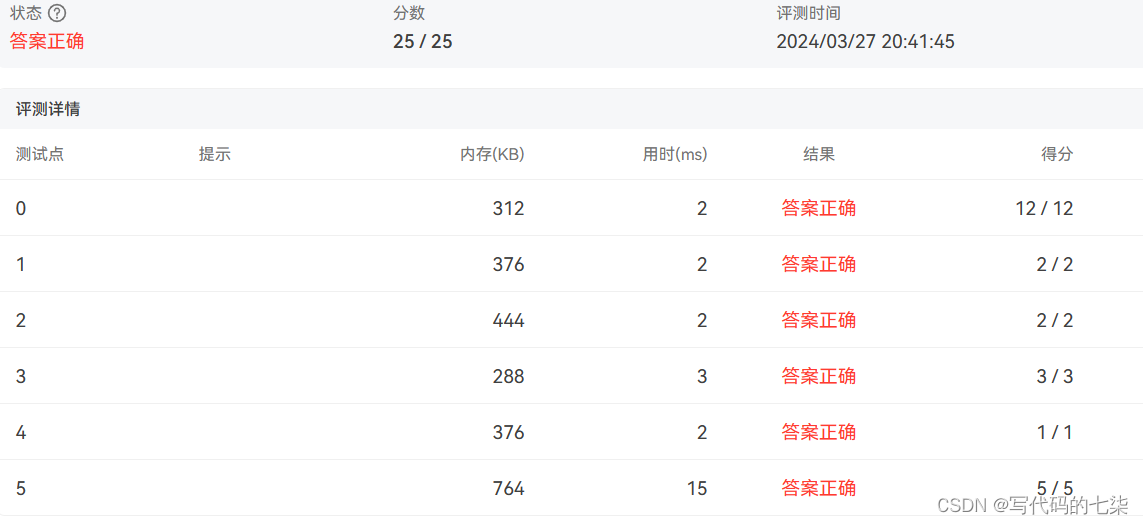
题目:猫粮规划


每种食物都有两种状态,记忆化dfs当然可以,但是你是否觉得这个题很想之前讲过的“小A点菜 ”?那道题问的是对于那些菜要花光她的钱,一共有多少方案?这道题问的是一个区间罢了,那么既然题目意思都这么像,跑不了解法也基本一致:
还是设置f[i][j]表示遍历i个东西获得j能量对应的方案数,
f[i][j]=f[i-1][j]+f[i-1][j-a[i]]
那么最终直接把符合题意的j全部加起来就行了。代码如下:(注意好初始化就行)
#include <bits/stdc++.h>
using namespace std;
int ans,n,l,r,a[50],f[50][500];
int main(){cin>>n>>l>>r;for(int i=1;i<=n;i++)cin>>a[i],f[i][0]=1;f[0][0]=1;for(int i=1;i<=n;i++)for(int j=0;j<=r;j++){f[i][j]=f[i-1][j];if(j-a[i]>=0)f[i][j]+=f[i-1][j-a[i]];}for(int j=l;j<=r;j++){ans+=f[n][j];}cout<<ans;
}既然看到转移仅用到了i-1行的数据,那么i放到外面就可以又降一维,变成这样:
for(int i=1;i<=n;i++)for(int j=r;j>=0;j--){if(j-a[i]>=0)f[j]+=f[j-a[i]];}就变成了如下的一维解法:
#include <bits/stdc++.h>
using namespace std;
int ans,n,l,r,a[50],f[500];
int main(){cin>>n>>l>>r;for(int i=1;i<=n;i++)cin>>a[i];f[0]=1;for(int i=1;i<=n;i++)for(int j=r;j>=a[i];j--){f[j]+=f[j-a[i]];}for(int j=l;j<=r;j++){ans+=f[j];}cout<<ans;
}