[优选算法专栏]专题十五：FloodFill算法(一)-编程知识

[优选算法专栏]专题十五：FloodFill算法(一)

本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：算法从入门到精通
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

专题十五

图像渲染
- 算法原理：
- 代码实现：
岛屿数量
- 算法原理：
- 代码实现：

图像渲染

题目来源：733.图像渲染

有一幅以 m x n 的二维整数数组表示的图画 image ，其中 image[i][j] 表示该图画的像素值大小。

你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行上色填充。

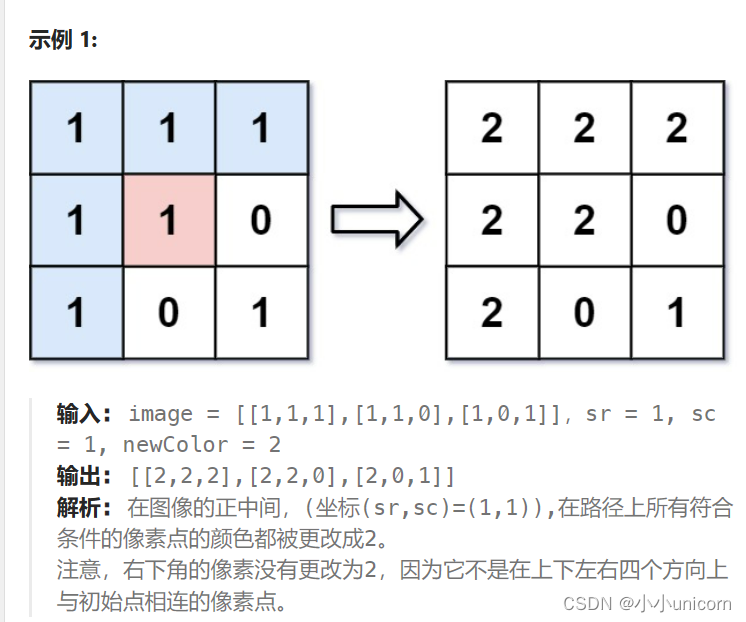
为了完成上色工作，从初始像素开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为 newColor 。

最后返回经过上色渲染后的图像。
在这里插入图片描述

算法原理：

本题要用BFS来解决此问题：
具体如下：
在这里插入图片描述

从给定位置开始，上下左右搜索为第一层。
从第一层两个位起点继续上下左右一层一层剥开。
依次内推…
当某一层上下左右搜索中，没有发现目标值就结束。

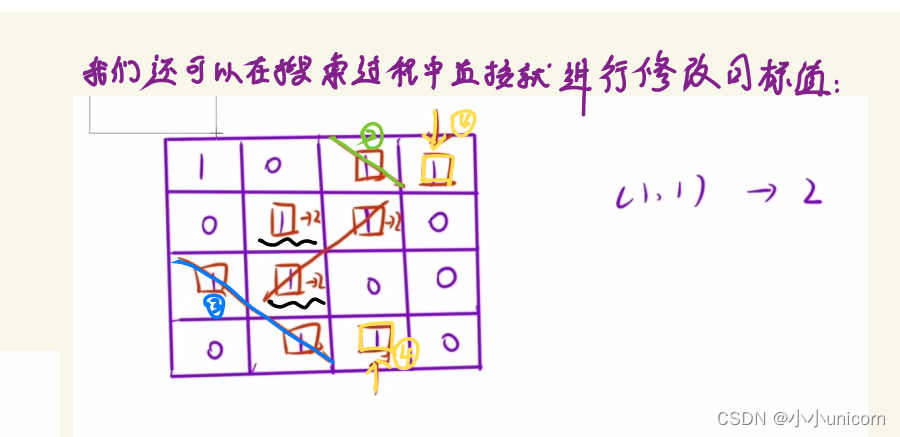
在上面搜索过程中，我们可以边在搜索过程中就进行修改，达到优化效果。

在这里插入图片描述

代码实现：

在代码实现之前，我们先做一下预处理。
通常BFS宽度优先遍历中，要对四个方向或者八个方向进行搜索，此时我们可以定义一个向量数组。
在这里插入图片描述
dx与dy为横坐标与纵坐标的偏移量。我们让坐标加上这个偏移量就是搜索后的宽度优先遍历的四个方向。

class Solution
{//存的是一个数对（坐标）typedef pair<int,int> PII;//向量数组int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};
public:vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {//先标记一下需要修改的像素值int prev=image[sr][sc];//处理边界情况：if(prev==color)return image;queue<PII> q;q.push({sr,sc});//获取起始点位置int m=image.size(),n=image[0].size();while(q.size()){auto [a,b]=q.front();q.pop();image[a][b]=color;for(int i=0;i<4;i++){int x=a+dx[i],y=b+dy[i];//防止越界if(x>=0&&x<m&&y>=0&&y<n&&y<n&&image[x][y]==prev){//满足情况入队q.push({x,y});}}}return image;}
};

岛屿数量

题目来源：岛屿数量
给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

在这里插入图片描述

算法原理：

题目很好理解：
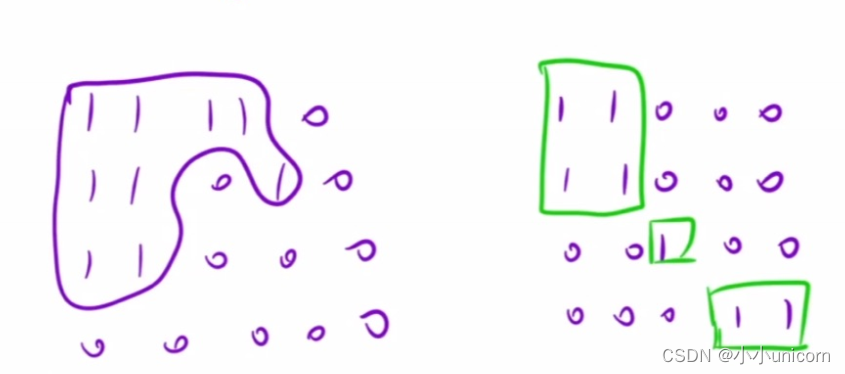
在这里插入图片描述
看到此类问题，首选BFS。
我们来模拟一下这个过程：

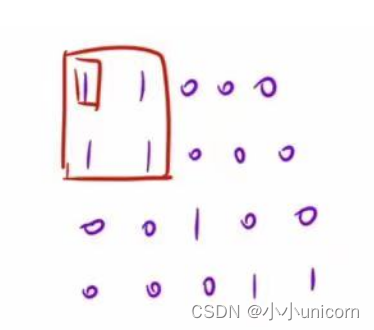
扫描矩阵，找到一个陆地的时候，就将这个陆地连接的联通快找到。怎么找用BFS。
此时找到一个岛屿，定义一个变量，让我们的ret++即可，但是有个问题：在我们层序遍历扩展到一个位置时，是不能让他拓展回去的。
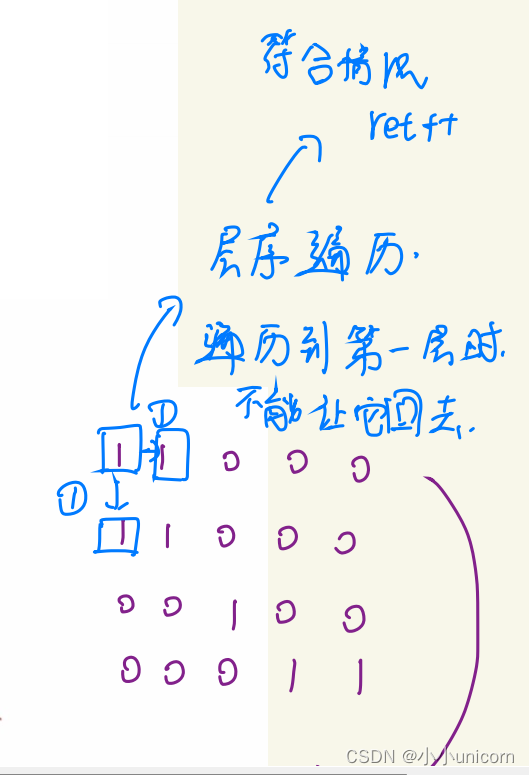
在这里插入图片描述
那么此时有两种办法：

在原数组进行修改
定义一个bool数组

第一种会修改原始数组的值，我们不推荐。
通常我们会采取第二种方式：
定义一个vis[m][n]数组：
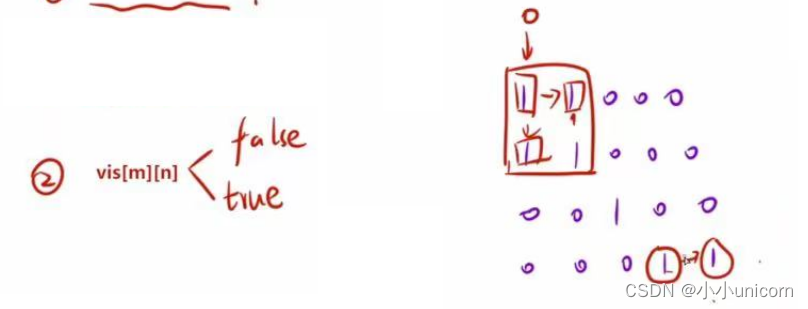
在这里插入图片描述
只要我们遍历过次位置，就将定义为true.数组还有个作用，当我们发现值为1，为true时ret不用++反之false就++。

代码实现：

class Solution 
{//向量数组int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};bool vis[301][301];int m,n;
public:int numIslands(vector<vector<char>>& grid){m=grid.size(),n=grid[0].size();int ret = 0;for(int i=0;i <m; i++){for(int j=0;j<n; j++){    if(grid[i][j]=='1' && vis[i][j]==false){   ret++;bfs(grid,i,j);// 把这块陆地全部标记一下了}}}return ret;}void bfs(vector<vector<char>>& grid,int i,int j){queue<pair<int, int>> q;q.push({i,j});vis[i][j]= true;while(q.size()){auto [a,b]=q.front();q.pop();for(int k=0;k<4;k++){int x=a+dx[k],y=b+dy[k];//防止越界if(x>=0&&x<m&&y>=0&&y<n&&y<n&&grid[x][y]=='1'&&vis[x][y]==false){//满足情况入队q.push({x,y});vis[x][y]=true;}}}}
};