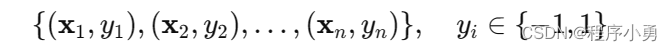Machine Learning机器学习之向量机（Support Vector Machine，SVM）-编程知识

目录

前言

算法提出背景：

核心思想：

原理：

应用领域：

一、支持向量机分类（主要变体）

二、构建常见的支持向量机模型

基于Python 中的 Scikit-learn 库构建线性支持向量机（SVM）

三、向量机应用案列（完整代码）

四、总结

优点：

缺点：

优化方向：

博主介绍：✌专注于前后端、机器学习、人工智能应用领域开发的优质创作者、秉着互联网精神开源贡献精神，答疑解惑、坚持优质作品共享。本人是掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战，深受全网粉丝喜爱与支持✌有需要可以联系作者我哦！

🍅文末三连哦🍅

👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟

前言

支持向量机（Support Vector Machine，SVM）是由Vladimir N. Vapnik等人于1990年提出的一种监督学习算法。它的核心思想是通过在特征空间中找到一个最优的超平面来进行分类，使得两个类别的样本之间的间隔最大化。SVM 在分类、回归分析、异常检测等领域都有着广泛的应用。

算法提出背景：

支持向量机最初是为了解决二分类问题而提出的。其发展背景主要源于统计学习理论和凸优化理论的发展。在提出之初，SVM 主要用于处理线性可分的数据集，后来又发展出了核技巧(kernel trick)，使其能够处理非线性分类问题。

核心思想：

SVM 的核心思想是找到一个最优的超平面，将不同类别的样本分隔开来，并且使得两个类别之间的间隔最大化。具体来说，SVM 算法的目标是找到一个决策边界（超平面），使得所有的样本点到这个边界的距离（即间隔）最大化。

原理：

间隔最大化： SVM 算法通过最大化分类边界与最近的训练样本点之间的间隔来实现分类。
支持向量： 在优化问题中，只有一部分训练样本点被称为支持向量，它们是离分类边界最近的样本点。
核技巧： SVM 使用核技巧来将线性分类扩展到非线性分类。核技巧是一种数学手段，可以在高维特征空间中进行计算，而不需要显式地计算高维空间中的特征向量。

支持向量机的原理的公式来描述：

对于二分类问题，给定一个训练数据集：

支持向量机的原理可以通过以下公式来描述：

对于二分类问题，给定一个训练数据集：

$\{(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \ldots, (\mathbf{x}_n, y_n)\}, \quad y_i \in \{-1, 1\}$

其中 ${x}_i$ 是输入样本的特征向量， $y_i$ 是对应的类别标签，取值为-1或 1。

我们的目标是找到一个超平面 $w^T \mathbf{x} + b = 0$ ，能够将两类样本分开，并且使得两个类别中距离超平面最近的样本点到超平面的距离最大。这个距离称为间隔（margin）。

应用领域：

分类问题： SVM 主要用于解决二分类问题，可以通过调整参数和选择合适的核函数来适应不同的数据特征。
回归分析： SVM 还可以应用于回归分析问题，称为支持向量回归（Support Vector Regression，SVR），通过最小化预测值与真实值之间的误差来拟合数据。
异常检测： SVM 还可以用于异常检测，通过找到与训练样本差异较大的数据点来识别异常。

一、支持向量机分类（主要变体）

向量机广泛应用于分类和回归分析的监督学习算法。

在支持向量机算法中，主要有以下几种主要的变体：

线性支持向量机（Linear SVM）： 最基本的支持向量机形式，用于处理线性可分或近似线性可分的数据。通过构建一个最大间隔超平面来分隔两个类别。

非线性支持向量机（Nonlinear SVM）： 通过使用核技巧（kernel trick），将数据映射到高维空间中进行分类，从而处理非线性可分的数据。常用的核函数包括多项式核、高斯核（径向基函数核）等。

支持向量回归（Support Vector Regression，SVR）： SVM 不仅可以用于分类问题，还可以用于回归分析。支持向量回归尝试通过最大化边界以外数据点的容忍度来拟合数据。

多类别支持向量机（Multiclass SVM）： SVM 最初是针对二分类问题的，但可以通过一对一（One-vs-One）或一对其他（One-vs-Rest）的策略来处理多类别分类问题。

增量式支持向量机（Incremental SVM）： 增量式支持向量机允许在训练数据集发生变化时对模型进行增量式的更新，而无需重新训练整个模型。

稀疏支持向量机（Sparse SVM）： 稀疏支持向量机通过引入稀疏性约束，以减少模型中使用的支持向量的数量，从而降低模型的复杂度。

二、构建常见的支持向量机模型

构建一个常见的支持向量机（SVM）网络通常涉及以下步骤：

数据准备： 准备用于训练和测试的数据集，包括特征和标签。确保数据集经过适当的预处理，如归一化、缺失值处理等。
模型选择： 选择合适的支持向量机模型，包括线性 SVM、非线性 SVM（使用核技巧）等，根据问题的性质选择合适的模型。
模型训练： 使用训练数据对支持向量机模型进行训练。训练过程主要包括优化超参数和拟合数据。
模型评估： 使用测试数据对训练好的模型进行评估，评估模型的性能指标如准确率、精确率、召回率、F1 值等。
模型调优： 根据评估结果调整模型的超参数或者进行特征选择等操作，进一步提高模型的性能。

基于Python 中的 Scikit-learn 库构建线性支持向量机（SVM）

# 导入必要的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 加载数据集（这里以鸢尾花数据集为例）
iris = datasets.load_iris()
X = iris.data
y = iris.target# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 特征标准化（对特征进行归一化处理）
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)# 初始化支持向量机模型
svm = SVC(kernel='linear', random_state=42)# 训练支持向量机模型
svm.fit(X_train, y_train)# 在测试集上进行预测
y_pred = svm.predict(X_test)# 计算模型准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

执行结果：精度为100%

三、向量机应用案列（完整代码）

基于支持向量机（SVM）可以用于图像分类任务，以下通过使用 SVM 对手写数字进行识别。

我们使用了 sklearn 中的手写数字数据集（Digits Dataset）。我们将数据集划分为训练集和测试集，并对特征进行了标准化处理。然后，我们初始化了一个支持向量机模型，并使用训练集对其进行训练。最后，在测试集上进行预测，并计算了模型的准确率。

需要注意的是选择了径向基函数核（RBF Kernel），这是一种常用的非线性核函数，适用于处理非线性分类问题，如图像分类。我们可以根据实际情况选组需要的函数核。

# 导入必要的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 加载手写数字数据集
digits = datasets.load_digits()# 获取特征和标签
X = digits.data
y = digits.target# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 特征标准化（对特征进行归一化处理）
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)# 初始化支持向量机模型
svm = SVC(kernel='rbf', random_state=42)# 训练支持向量机模型
svm.fit(X_train, y_train)# 在测试集上进行预测
y_pred = svm.predict(X_test)# 计算模型准确率
accuracy = accuracy_score(y_test, y_pred)
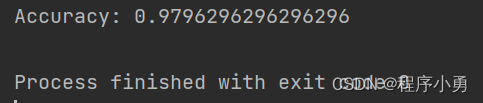
print("Accuracy:", accuracy)

执行结果：精度约为98%