一 相关性分析
相关性分析一般是用来简单的分析数据之间的相关性关系,用来研究的是连续性的数值变量或者量表的数据,只能分析出来每两个变量之间的相关性关系。一般是用于在回归分析之前,用于对于数据进行一个简单的相关性探讨,回归分析说明的是数据之间的因果关系。
spss---分析---相关---双变量
Pearson系数:叫皮尔逊相关系数,也叫线性相关系数,用于进行线性相关分析,是最常用的相关系数,当数据满足正态分布时会使用该系数。
Spearman系数:当数据不满足正态分布时,使用该系数。
Kendall系数:通常用于评分数据一致性水平研究(非关系研究)
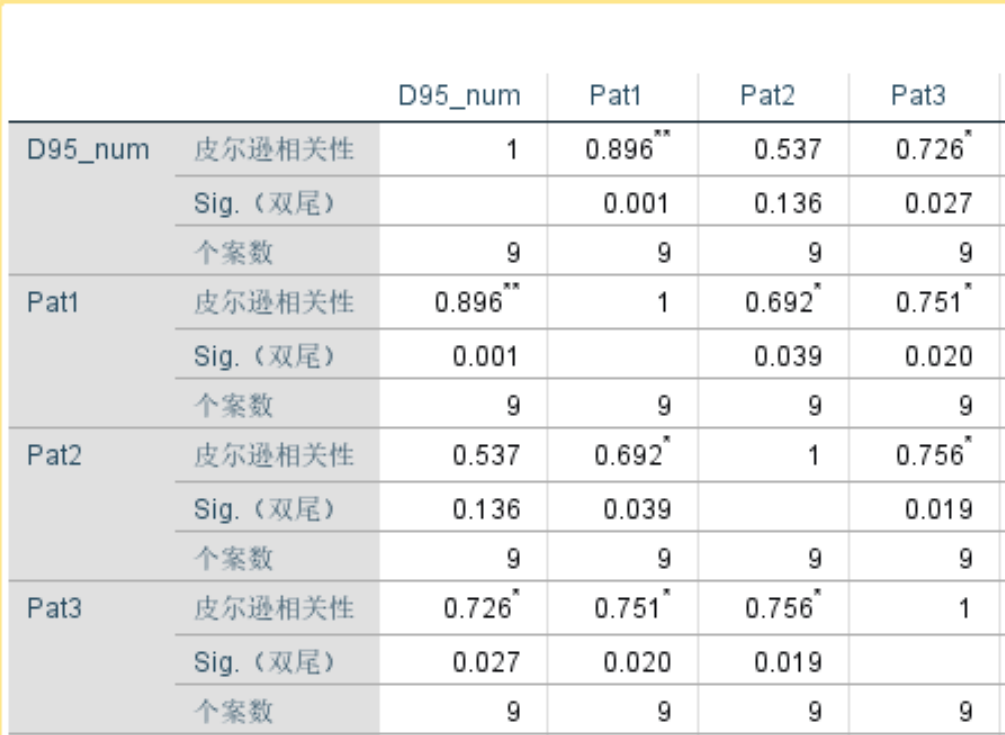
**代表P小于0.01,*代表P小于0.05
相关系数r的绝对值一般在0.8以上,认为A和B有强的相关性。0.3到0.8之间,可以认为有弱的相关性。0.3以下,认为没有相关性。 一般0.7以上说明关系非常紧密;0.4~0.7之间说明关系紧密;0.2~0.4说明关系一般。
数值的正负代表相关是正向相关或者负向相关。
二 回归分析
spss---分析---回归----线性
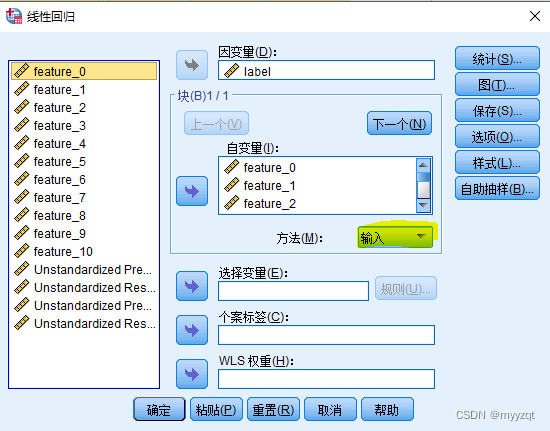
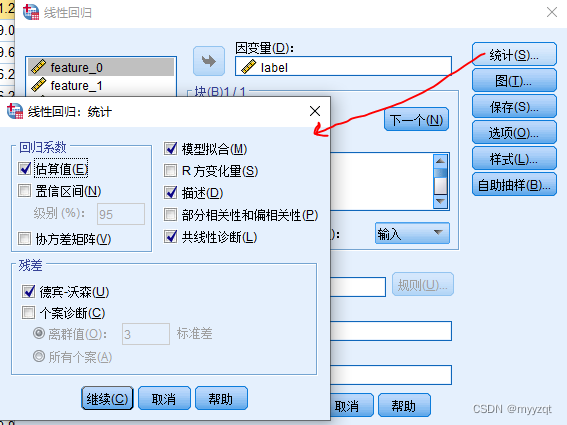
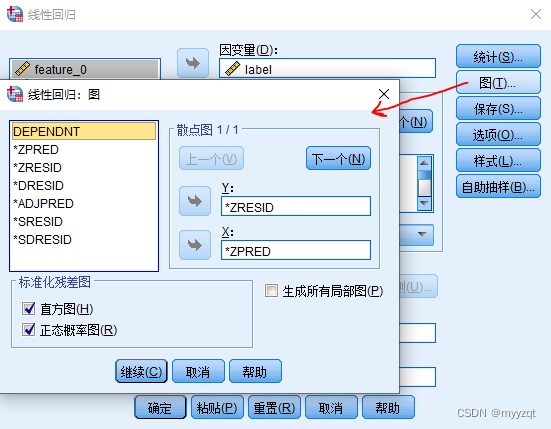
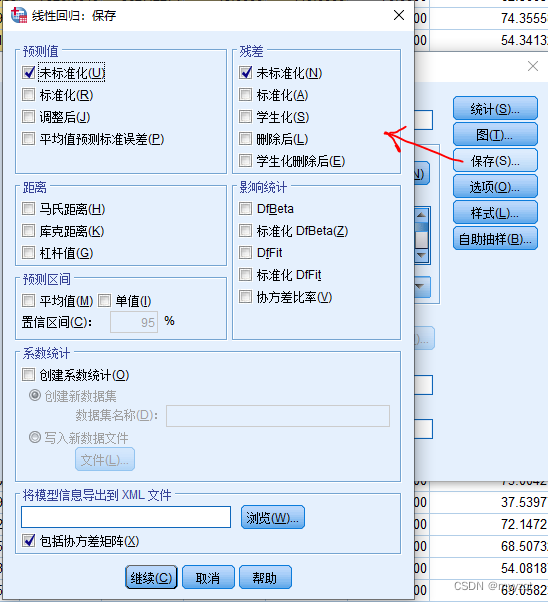
结果解读:
第一,R方结果和残差独立性检验(德宾沃森检验):
模型摘要是判断两者之间线性关系的重要指标,也反映了回归的拟合程度。
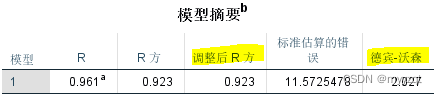
①一般情况下,R²看的是“调整R²”,该值相对不受自变量个数的影响,结果更为可靠。R平方即R的平方,又可以叫判定系数、拟合优度,取值范围是[0,1],R平方值越大,表示模型拟合的越好。一般大于70%就认为拟合的不错,60%以下的就需要修正模型了。这个案例里R平方0.923,表明“所有自变量” 解释“训练比赛满意感”的92.3%变异。
②德宾沃森检验若结果在0-4之间,基本可认为数据独立性符合。本例的德宾沃森值为2.027,符合独立性。
第二个结果为方差分析(ANOVA):
主要探讨模型的是否成功建成。
本案例F=24.464,P<0.001,说明至少有一个自变量解释了一部分的因变量的变异,从而使得回归变异变大,残差变异减少,模型成功建立。
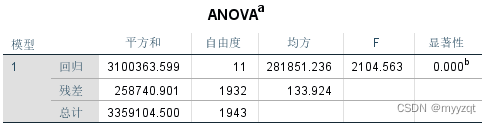
值得注意的是,本题“平方”和即变异程度(离均差平方和),R²=回归变异平方和/总的平方和=3100363.599/3359104.500=0.923。因此方差分析和R²结果同出一源,方差分析侧重于分析模型是否成功,R²侧重于探讨模型有多成功(相当于效应量)。
F检验主要是检验因变量与自变量之间的线性关系是否显著,用线性模型来描述他们之间的关系是否恰当,越小越显著。这个案例里F值很小,说明因变量与自变量之间显著。说明多重线性回归模型中至少有一个自变量的系数不为零。同时,回归模型有统计学意义也说明相较于空模型,纳入自变量有助于预测因变量,或说明该模型优于空模型。
第三个结果,回归分析的主要结果:
计算回归系数、并对回归系数进行假设检验,探讨影响因素。
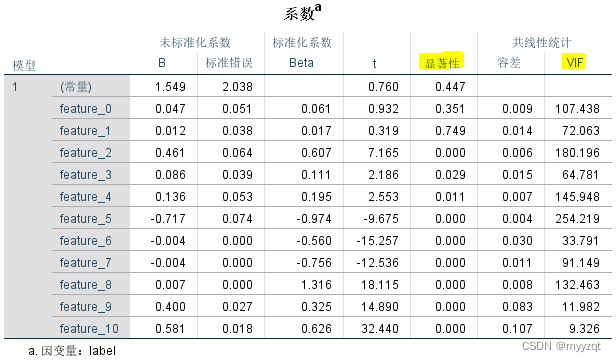
重点关注P-value,也就是P值,用来检验回归方程系数的显著性,又叫T检验,T检验看P值,是在显著性水平α(常用取值0.01或0.05)下F的临界值,一般以此来衡量检验结果是否具有显著性,如果P值>0.05,则结果不具有显著的统计学意义,如果0.01<P值<0.05,则结果具有显著的统计学意义,如果P<=0.01,则结果具有极其显著的统计学意义。T检验是看某一个自变量对于因变量的线性显著性,如果该自变量不显著,则可以从模型中剔除。
系数的正负代表了对应的特征向量时正向预测还是负向预测label。
共线性统计包括方差膨胀因子(VIF)和容差两个指标,事实上,VIF=容差的倒数(1/容差),只需要判断其中一个指标即可。如果容忍度小于0.1(或方差膨胀因子大于10),提示数据存在多重共线性。多重共线性可以考虑stepwise 回归或者岭回归。
第四个结果,由于本例选择计算残差和预测值,可以通过下表来看预测值和残差结果

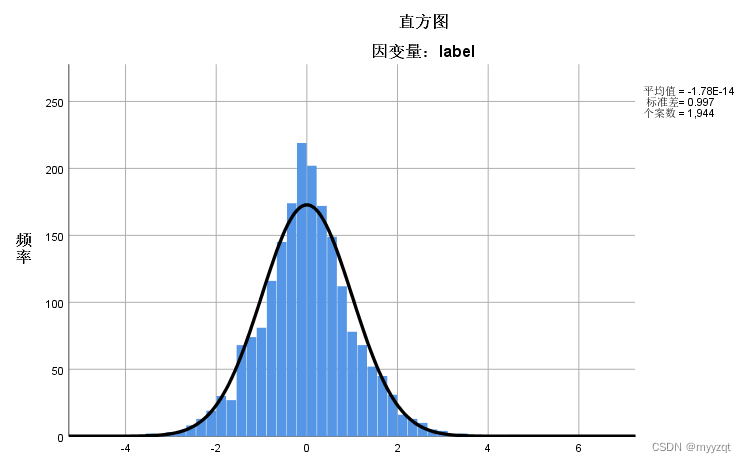
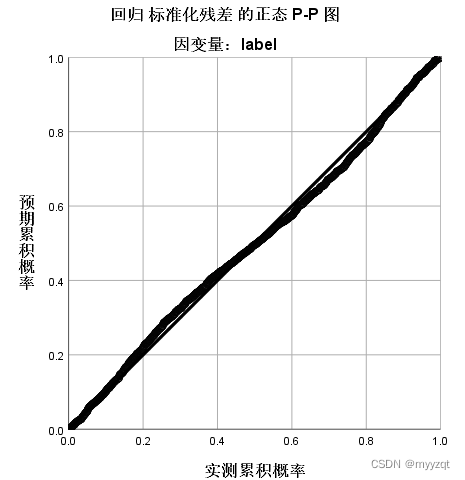
第五个结果,残差直方图和P-P图。
可以看出,本例残差直方图服从正态分布,且均数接近于0,标准差接近于1(标准正态分布),这意味着线性回归在正态性条件是达到的。P-P图也表明满足正态性条件。
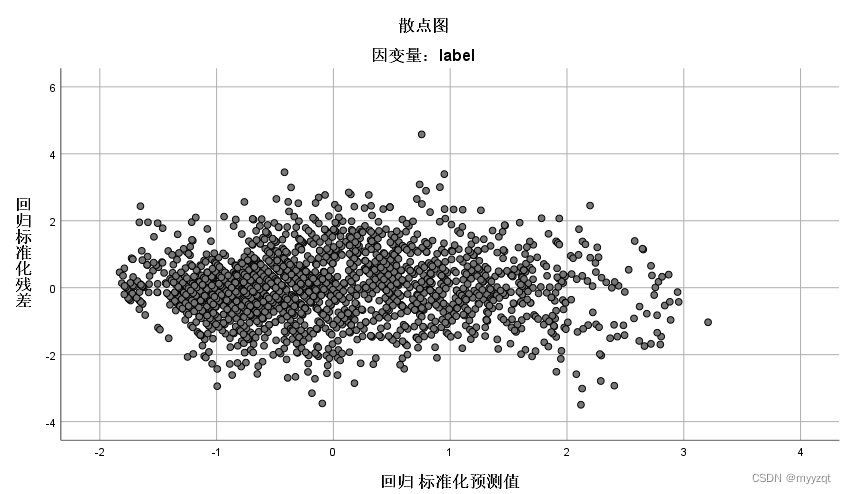
第六个结果,残差图。
残差图的x、y轴分别是因变量预测值的标准化值和残差的标准化值(一般x轴是预测值的标准化值)。本例从图形来看,标准化残差图分布在0值周围,基本是上下对称分布,分布特征不随预测值的增加而发生改变,意味着数据方差齐性、独立性条件符合。
使用excel做回归分析
数据---数据分析
如果没有数据分析,则File---option添加数据分析
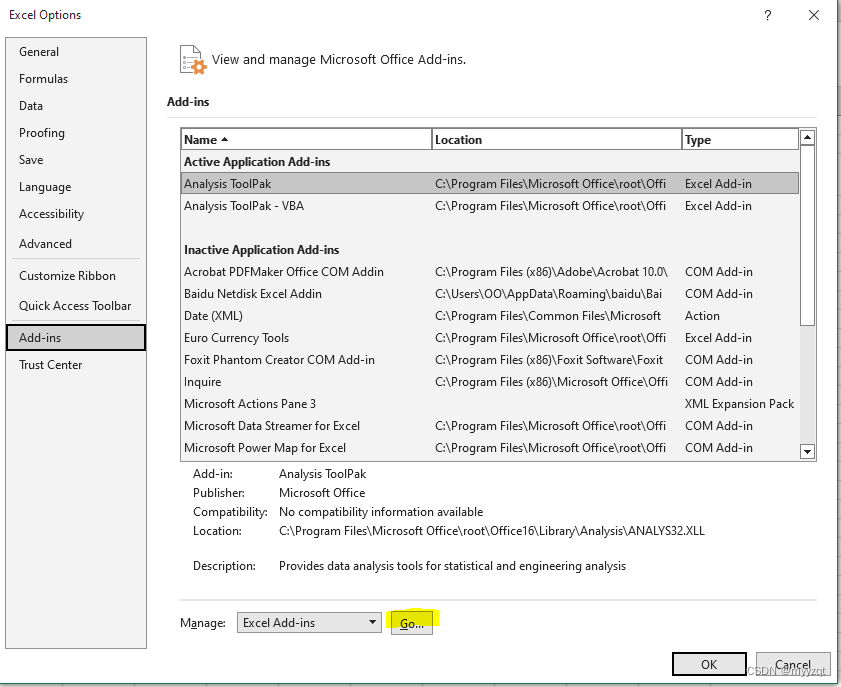
结果如下所示:各参数的意义与spss得到的一样