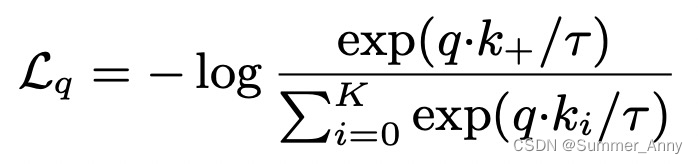数据结构/C++:位图 & 布隆过滤器
- 位图
- 实现
- 应用
- 布隆过滤器
- 实现
- 应用
哈希表通过映射关系,实现了O(1)的复杂度来查找数据。相比于其它数据结构,哈希在实践中是一个非常重要的思想,本博客将介绍哈希思想的两大应用,位图与布隆过滤器。
位图
看到以下题目:
给40亿个无序不重复的无符号整数(unsigned int)。如何判断一个数字是否在这40亿个数字之中?
大部分人拿到这道题,也许会想到map,set,哈希这样的容器。但是其有40亿个数据,而且是整型,最后估算下来,光是数据就占用了十多个G,何况还要用红黑树,哈希表这样的结构存储下来,这是不现实的。
仔细想想,对于这道题目而言,一个数据只有两种状态:在/不在。如果我们想要标识两种状态,其实只需要一个比特位就够了,0表示不存在,1表示存在。通过哈希的映射思想,我们可以把每一个数据映射到一个比特位中,这就是位图的概念。
在STL库中,已经为我们提供了位图bitset,我先简单讲解一下bitset的接口,再给大家实现一个位图。

在bitset中,存在着一个非类型模板参数N,其代表位图中要开多少个比特位。
| 接口 | 功能 |
|---|---|
operator[] | 返回对应位置的引用 |
count | 计算所有比特位中1的个数 |
size | 返回比特位的个数 |
test | 检测某一个位,是1返回true,是0返回false |
set | 把某一个位的值改为1 |
reset | 把某一个位的值改为0 |
实现
基本框架如下:
template<size_t N>
class bitSet
{
public:private:vector<int> _bits;
};
我们把位图做成了一个模板,模板参数N用于传参,代表要开几个位。那么我们要如何开出N个比特位?其实我们可以用一个int类型的数组vector,一个int有32bit,那么我们开出来的元素个数就是N / 32个。但是由于C++的除法会向下取整,所以我们要额外+1,避免开出来的位不够。这样我们就可以写一个构造函数:
template<size_t N>
class bitSet
{
public:bitSet(){_bits.resize(N / 32 + 1, 0);}private:vector<int> _bits;
};
接着我们来实现bitset中最重要的几个接口:
set:
set接口的功能是把指定的位改为1。
现在传进来一个整数x,我们要如何定位到它属于vector中哪一个元素的哪一个位呢?
其实也很简单,一个元素有32bit,那么我们让x / 32就可以得到其对应的整数了。至于它在整数的第几位,那就是x % 32。
size_t i = x / 32; // vector的第i个元素
size_t j = x % 32; // 第i个元素的第j个比特位
现在我们的任务就是把第i个元素的第j个比特位变成1。我们可以把数字1左移j位,然后让_bits[i]与左移后的值按位或。这样就不会影响到其他位,还能把目标位变为1。
比如把11001100的第4位变为1:
11001100 //待修改数据00000001 //数字100010000 //数字1左移4位
------------11001100| 00010000 //按位或------------11011100
可以看到,我们确实把11001100的第4位变为1了。
set接口如下:
void set(size_t x)
{assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] |= (1 << j);
}
reset:
reset接口的功能是把指定的位改为0。
通过之前同样的办法,定位到第i个元素的第j位,接下来的任务就是把第i个元素的第j位变为0。想要让一个位变为0,只要让它按位与上0就可以了,但是我们其它的位不能变,要按位与1。也就是说我们要拿到第j位为0,其它位为1的数据。
我们之前通过数字1的左移,可以拿到第j位为1,其他位为0的数据。那么我们直接取反,就可以得到第j位为0,其它位为1的数据了。
代码如下:
void reset(size_t x)
{assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);
}
test:
test接口的功能是检测指定位的值是0还是1。
我们直接让1左移j位,按位与就行了,代码如下:
bool test(size_t x)
{assert(x <= N);size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);
}
这就是位图最重要的三个操作了,整体还是非常简单的。至于其他接口,都只是锦上添花的作用,而且实现起来也很简单,这里不做讲解了。
位图在处理大量数据时,有非常明显的优势,其主要功能如下:
- 标识一个数据的状态
- 以O(1)的复杂度查找一个数据的状态
- 排序 + 去重
应用
我们再看到几个题目,来加深对位图的理解:
给两个文件,分别有100亿个整数(unsigned int),我们只有1G内存,如何找到两个文件的交集?
根据估算,一个文件的大小大约就在37G,这是不可能放进内存中直接比较的,因此我们可以考虑位图。因为所有数据都是整数,所以数据范围在0 - 42亿之间,我们要开42亿个位。经过计算,42亿bit,大概也就是0.48GB,对于内存而言,还是很友好的。
我们分别把两个文件的数据分别插入到两个位图中,此时我们就有两个范围是0 - 42亿数的位图了,总共也就是0.96GB,在1G限制范围内。然后我们再遍历两个位图,分别对比每一个位,只要两张位图该位都是1,那就是文件的交集。
一个文件有100亿个整数(int),设计算法找到出现次数不超过2次的所有整数
先前我们通过一个比特位标识了一个数据在与不在,但是此题总数据存在多种状态:不存在,存在一个,存在两个以上三种状态。按照位图的思想,标识三种状态,至少需要2bit,比如00表示不存在,01表示存在一个,10表示存在两个及以上。这样我们就可以设计算法了:
template<size_t N>
class two_bit_set
{
public:void set(size_t x){//00 -> 01if (_bs1.test(x) == false&& _bs2.test(x) == false){_bs2.set(x);}//01 -> 10else if (_bs1.test(x) == false&& _bs2.test(x) == false){_bs1.set(x);_bs2.reset(x);}//10 -> 不处理}int test(size_t x){if (_bs1.test(x) == false&& _bs2.test(x) == false){return 0;}else if (_bs1.test(x) == false&& _bs2.test(x) == false){return 1;}else{return 2;//出现2次以上}}private:bitset<N> _bs1;bitset<N> _bs2;
};
以上代码中,我们在类中定义了两个位图,两个位图的同一个位用于标识一个数据的不同状态,这样就可以区分数据的情况了。
以此类推,当我们发现一张位图无法标识一个数据的状态数目时,就可以用多张位图组合。
布隆过滤器
假设某个游戏公司,在开服第一天因为过于火爆,有大量的玩家同时注册游戏,这给后台游戏服务器造成了大量压力。其中一个问题就是:游戏要求玩家之前不能有重复的名字,但是每次玩家输入一个名字的时候,都要去后台的数据库查询这个名字存不存在。这导致数据库访问非常迟缓,请问要如缓解这个问题?
以上问题在于,每当一个玩家输入一个名称(字符串),都要去数据库查询,看是否存在相同的名字。有没有办法能够快速查询到一个名字是否重复呢?这就不得不提布隆过滤器了。
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概
率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存
在”,它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
现在我们有一下字符串:
"Hello python""Hello C++""Hello C#""Hello Go""Hello CSDN"
假设我们现在有一个位图,接着我们把每一个字符串映射到位图中,我们是否可以通过位图来判定一个字符串存不存在呢?这是不准确的,因为两个字符串有可能会被映射到同一个位上,这就会导致误差,于是布隆觉得,我们能不能把误差降到非常低呢?
于是布隆过滤器的思想就诞生了:
把一个数据通过三套不同的哈希函数,映射到三个位上
当我们查找数据的时候,只有这个数据上的三个位都为1,才说明这个数据存在。
比如这样:
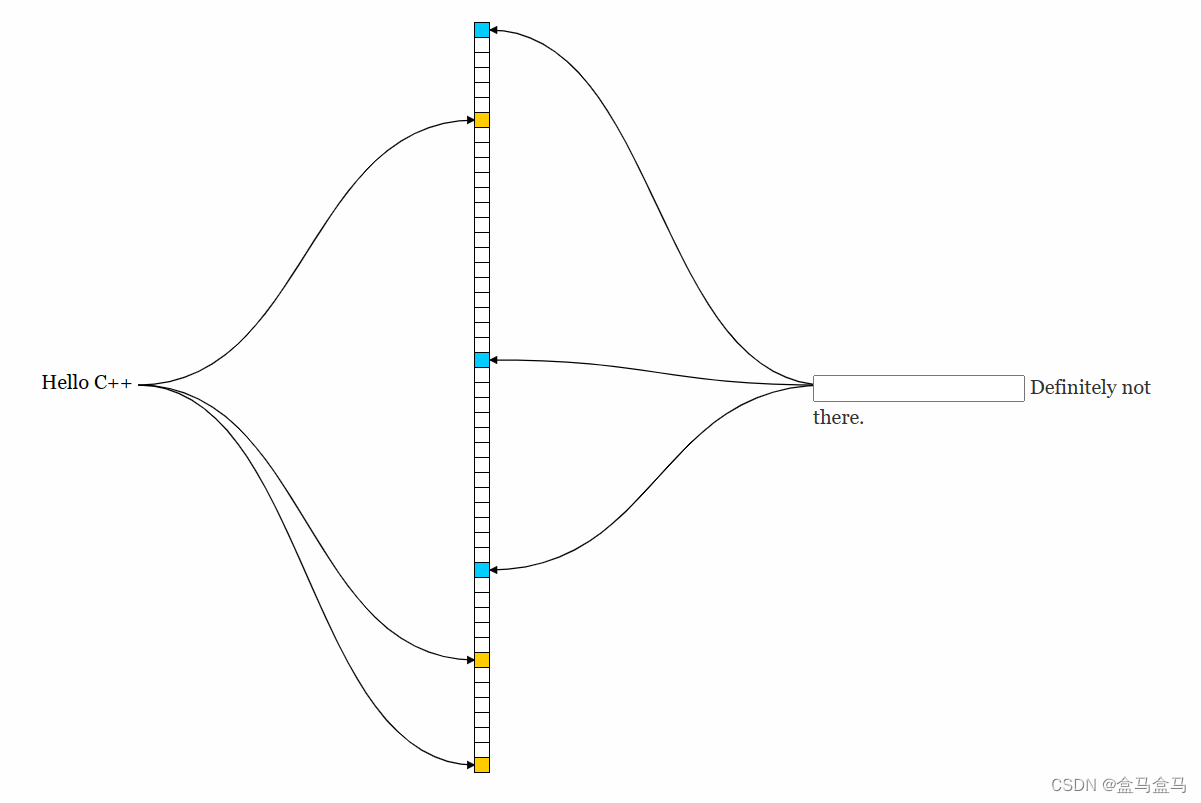
图中竖着的长条,是一个位图,我们输入了一个Hello C++字符串,然后通过三种不同的哈希函数,把这个字符串映射到了三个不同的位上。
接着我们再插入一个Hello python:
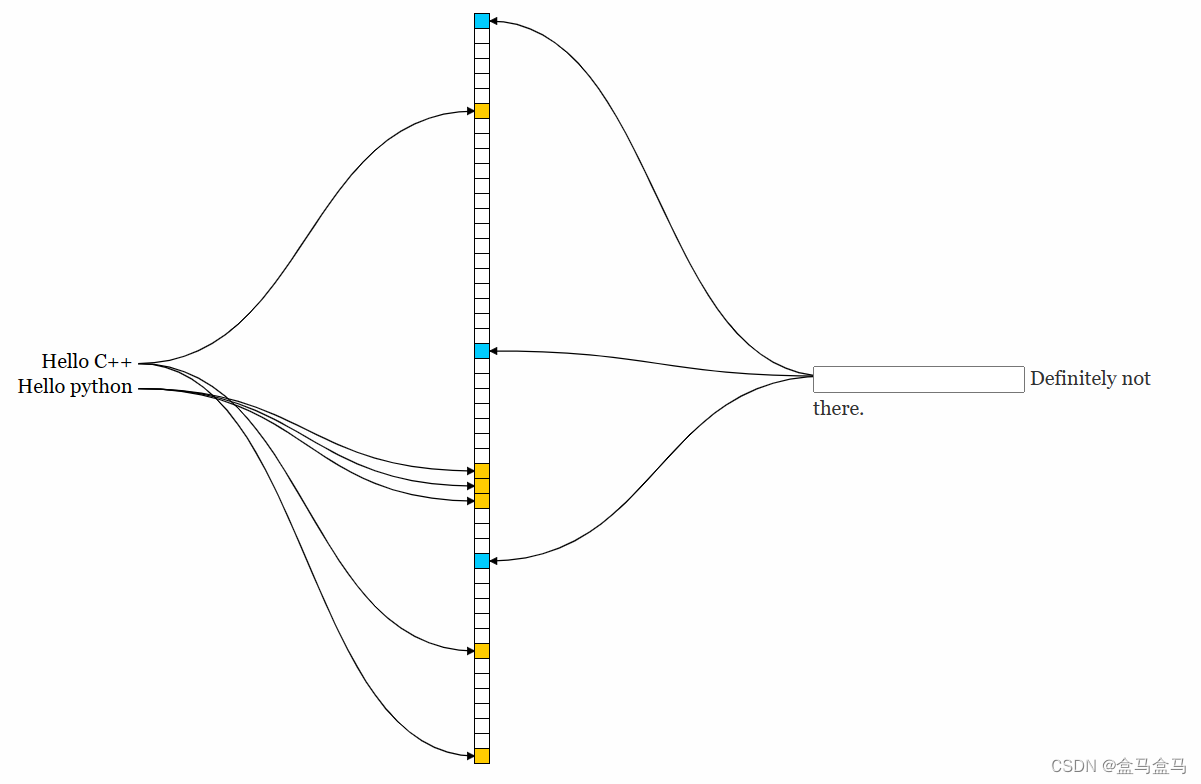
Hello python也映射到了三个位,而且没有与Hello C++发生重复。但是也有特殊的情况,比如我再插入Hello Go:
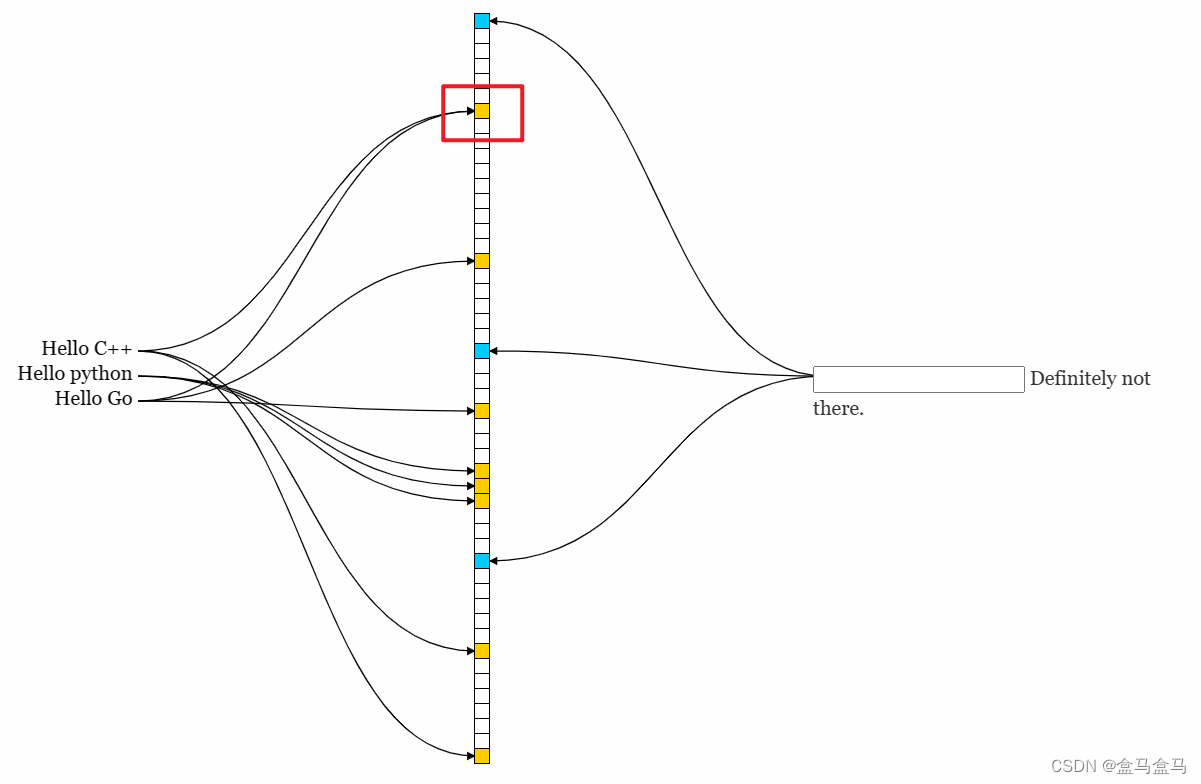
可以看到,Hello C++与Hello Go有一个位发生了重复,这会不会造成数据的误判呢?答案是不会的,因为这两个字符串的另外两个位不同,只有一个字符串的三个位都存在,才说明这个字符串有可能存在,比如我现在查询Hello CSDN是否在位图中:
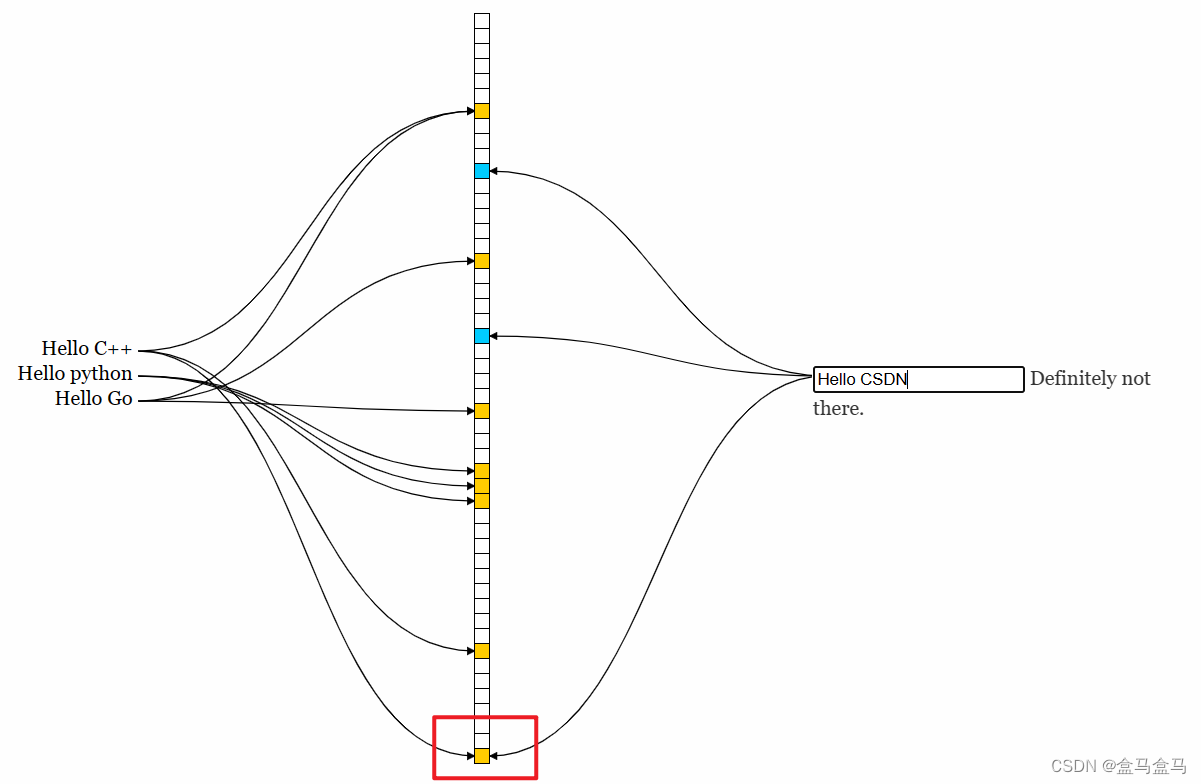
可以看到,Hello CSDN这个字符串,也映射到了三个位,其中有一个位是1,而另外两个位是0,只要有一个位对不上,就说明这个字符串一定不存在。因此Hello CSDN不存在在位图中。
接下来我们就来实现一个这样的布隆过滤器:
实现
哈希函数:
这里我们需要用到三个字符串 -> 整型的哈希函数,这里我取用了目前经过研究效果比较好的三个算法:BKDR,AP,DJB
struct HashFuncBKDR
{//BKDRsize_t operator()(const string& s){size_t hash = 0;for (auto ch : s){hash += ch;hash *= 131;}return hash;}
};struct HashFuncAP
{//APsize_t operator()(const string& s){size_t hash = 0;int i;for (i = 0; i < s.size(); i++){if ((i & 1) == 0)// 偶数位字符hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));else//奇数位字符hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));}return hash;}
};struct HashFuncDJB
{//DJBsize_t operator()(const string& s){register size_t hash = 5381;for (auto ch : s)hash = hash * 33 ^ ch;return hash;}
};
这个算法的内部实现并不重要,我们只需要知道,它们是三套不同的规则,可以把一个字符串映射到三个不同的位上。
基本结构:
template<size_t N,class K = string,class Hash1 = HashFuncBKDR,class Hash2 = HashFuncAP,class Hash3 = HashFuncDJB>
class BloomFilter
{
public:private:bitset<5 * N> _bs;
};
布隆过滤器BloomFilter有五个模板参数,N代表要插入的数据个数,K代表要处理的类型,剩下三个是不同的哈希函数,用于映射不同的位。
假设x为哈希函数的个数,m是布隆过滤器的长度,n是插入元素的个数,经过研究发现,三者满足以下关系式时,布隆过滤器的误判率最低:
x = m n ln 2 x=\frac{m}{n} \ln 2 x=nmln2
此处,我们的哈希函数x = 3,那么我们的m大约是n的4.3倍。因此在哈希函数为3个的情况下,布隆过滤器的长度最好是插入数据个数的4.3倍。此处我们取整数5倍,因此有bitset<5 * N> _bs;。
Set接口:
想要插入一个数据,其实就是通过三个哈希函数计算出三个映射位置,并把它们设置为1。
代码如下:
void Set(const K& key)
{size_t hash1 = Hash1()(key) % (5 * N);size_t hash2 = Hash2()(key) % (5 * N);size_t hash3 = Hash3()(key) % (5 * N);_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);
}
Test接口:
想要检测一个数据是否存在,就是检测出这个数据对应的三个映射位置是否都是1。
代码如下:
bool Test(const K& key)
{size_t hash1 = Hash1()(key) % (5 * N);if (_bs.test(hash1) == false)return false;size_t hash2 = Hash2()(key) % (5 * N);if (_bs.test(hash2) == false)return false;size_t hash3 = Hash3()(key) % (5 * N);if (_bs.test(hash3) == false)return false;return true; // 存在误判
}
布隆过滤器不能轻易地删除一个数据,比如以下情况:
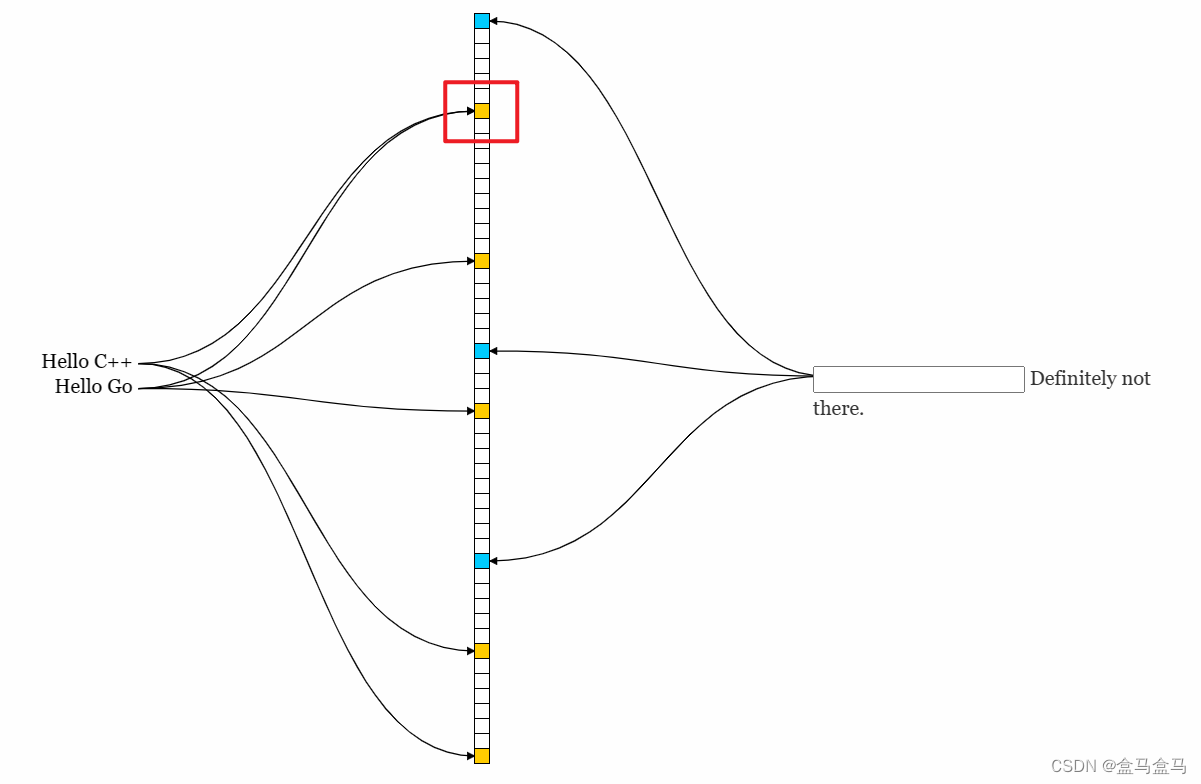
字符串Hello C++与Hello Go有一个位重复了,如果我们贸然删掉字符串Hello Go,那么就会导致Hello C++有一个位丢失了,那么我们不仅查找不到被删除的Hello Go,也查找不到Hello C++了。因此布隆过滤器不支持删除操作。
应用
布隆过滤器有以下特性:
- 如果检测到一个数据不存在,那么这个数据一定不存在
- 如果检测到一个数据存在,那么这个数据有可能存在
布隆过滤器最大特点就在于可以100%检测一个数据的不存在。那么我们回到最开始的问题:
每当一个玩家输入一个名称(字符串),都要去数据库查询,看是否存在相同的名字。有没有办法能够快速查询到一个名字是否重复呢?
我们可以把所有名字映射到布隆过滤器中,所有玩家输入一个字符串后要经过以下过程:
- 检测该字符串在不在布隆过滤器中
- 如果不存在,说明这个字符串一定不存在,此时直接返回结果,告诉玩家该名称可用
- 如果存在,说明这个字符串可能存在,此时再到数据库中去查找
布隆过滤器之所以叫做过滤器,就在于它可以过滤掉所有不存在的情况。
不妨想象一下,现在让两个人给自己的游戏账号取一个名字,它们重复的概率有多高呢?其实很低了。如果一个用户输入一个游戏名称,有80%的概率是不重复的,那么布隆过滤器就可以过滤掉80%的访问量,给数据库降低80%的压力。而且布隆过滤器搜索的时间复杂度仅仅为O(1),可见布隆过滤器有多么强大。