刚刚，百度和苹果宣布联名-编程知识

百度 × Apple

就在刚刚，财联社报道，百度将为苹果今年发布的 iPhone16、Mac 系统和 iOS18 提供 AI 功能。

苹果曾与阿里以及另外一家国产大模型公司进行过洽谈，最后确定由百度提供这项服务，苹果预计采取 API 接口的方式计费。

苹果将国行 iPhone 等设备采用国产大模型 AI 功能主要出于合规需求，因为苹果自身短期内还无法解决合规问题，但国外版 iPhone 等设备 AI 功能均来自苹果自己的大模型。

不是黑百度（我们要正视客观差距），相信大多数国行用户心理多少有点不是滋味，国产苹果味 🤣

为什么说大多数，而不是所有国行用户，剩下的小部分是什么人。

是持有「百度」股票的国行用户：

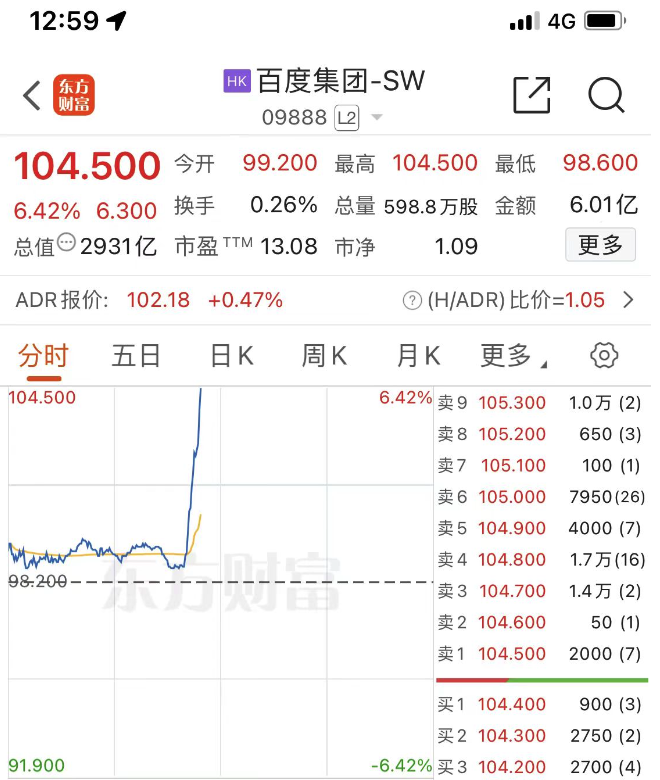
蹭上了果链，百度盘中上涨 6 个点。

本文发出的时候，H 股那边还没收盘，但基本可以断定结局。

中国公司，不管你是 A 股、H 股还是美股，都自带「出利好 = 高开低走」的传统艺能。

关于「百度」和「Apple」本次联名，你怎么看？是否会考虑放弃保修买入海外版？

...

回归主线。

来做一道和「百度」社招相关的算法面试题。

题目描述

平台：LeetCode

题号：649

Dota2 的世界里有两个阵营：Radiant（天辉）和 Dire（夜魇）。

Dota2 参议院由来自两派的参议员组成，现在参议院希望对一个 Dota2 游戏里的改变作出决定，他们以一个基于轮为过程的投票进行。

在每一轮中，每一位参议员都可以行使两项权利中的一项：

禁止一名参议员的权利：参议员可以让另一位参议员在这一轮和随后的几轮中丧失所有的权利。
宣布胜利：如果参议员发现有权利投票的参议员都是同一个阵营的，他可以宣布胜利并决定在游戏中的有关变化。

给你一个字符串 s 代表每个参议员的阵营。字母 'R' 和 'D'分别代表了 Radiant（天辉）和 Dire（夜魇）。

然后，如果有 n 个参议员，给定字符串的大小将是 n。

以轮为基础的过程从给定顺序的第一个参议员开始到最后一个参议员结束，这一过程将持续到投票结束，所有失去权利的参议员将在过程中被跳过。

假设每一位参议员都足够聪明，会为自己的政党做出最好的策略，你需要预测哪一方最终会宣布胜利并在 Dota2 游戏中决定改变。

输出应该是 "Radiant" 或 "Dire"。

示例 1：

输入：s = "RD"

输出："Radiant"

解释：
第 1 轮时，第一个参议员来自 Radiant 阵营，他可以使用第一项权利让第二个参议员失去所有权利。
这一轮中，第二个参议员将会被跳过，因为他的权利被禁止了。
第 2 轮时，第一个参议员可以宣布胜利，因为他是唯一一个有投票权的人。

示例 2：

输入：s = "RDD"

输出："Dire"

解释：
第 1 轮时，第一个来自 Radiant 阵营的参议员可以使用第一项权利禁止第二个参议员的权利。
这一轮中，第二个来自 Dire 阵营的参议员会将被跳过，因为他的权利被禁止了。
这一轮中，第三个来自 Dire 阵营的参议员可以使用他的第一项权利禁止第一个参议员的权利。
因此在第二轮只剩下第三个参议员拥有投票的权利,于是他可以宣布胜利

提示：

senate[i] 为 'R' 或 'D'

基本分析

整理题意：每次选择对方的一个成员进行消除，直到所有剩余成员均为我方时，宣布胜利。

由于每个对方成员执行权利都意味着我方损失一名成员，因此最佳方式是 「尽量让对方的权利不执行，或延迟执行（意味着我方有更多执行权利的机会）」。因此，最优决策为 「每次都选择对方的下一个行权成员进行消除」。

贪心

这个找“最近一个”对方行权成员的操作既可以使用「有序集合」来做，也可以使用「循环队列」来做。

先说使用「有序集合」的做法。

起始我们先将 s 中的 Radiant 和 Dire 分别存入有序集合 rs 和 ds 当中，然后从前往后模拟消除过程，过程中使用 idx 代表当前处理到的成员下标，使用 set 记录当前哪些成员已被消除。

当轮到 s[idx] 行权时（若 s[idx] 已被消除，则跳过本轮），从对方的有序队列中取出 「首个大于等于 idx 的下标」（取出代表移除）；若对方的有序序列不存在该下标，而行权过程又是循环进行的，说明此时下一个行权的对方成员是 「首个大于等于」 的下标，我们对其进行取出消除，随后往后继续决策。

Java 代码：

class Solution {
    public String predictPartyVictory(String s) {
        TreeSet<Integer> rs = new TreeSet<>(), ds = new TreeSet<>();
        int n = s.length();
        for (int i = 0; i < n; i++) {
            if (s.charAt(i) == 'R') rs.add(i);
            else ds.add(i);
        }
        Set<Integer> set = new HashSet<>();
        int idx = 0;
        while (rs.size() != 0 && ds.size() != 0) {
            if (!set.contains(idx)) {
                TreeSet<Integer> temp = null;
                if (s.charAt(idx) == 'R') temp = ds;
                else temp = rs;
                Integer t = temp.ceiling(idx);
                if (t == null) t = temp.ceiling(0);
                set.add(t);
                temp.remove(t);
            }
            idx = (idx + 1) % n;
        }
        return rs.size() != 0 ? "Radiant" : "Dire";
    }
}

不难发现，虽然将所有成员存入有序集合和取出的复杂度均为，但整体复杂度仍是大于。

因为我们在每一轮的消除中，从 idx 位置找到下一个决策者，总是需要遍历那些已被消除的位置，而该无效遍历操作可使用「循环队列」优化。

优化

使用循环队列 rd 和 dd 来取代有序集合 rs 和 ds。起始将各个成员分类依次入队，每次从两队列队头中取出成员，假设从 rs 中取出成员下标为 a，从 dd 中取出成员下标为 b，对两者进行比较：

若有 a < b，说明 a 先行权，且其消除对象为 b， a 行权后需等到下一轮，对其进行大小为的偏移后重新添加到 rd 尾部（含义为本次行权后需要等到下一轮）；
若有 b < a，同理，将 a 消除后，对 b 进行大小为的偏移后重新添加到 dd 尾部。

Java 代码：

class Solution {
    public String predictPartyVictory(String s) {
        Deque<Integer> rd = new ArrayDeque<>(), dd = new ArrayDeque<>();
        int n = s.length();
        for (int i = 0; i < n; i++) {
            if (s.charAt(i) == 'R') rd.addLast(i);
            else dd.addLast(i);
        }
        while (rd.size() != 0 && dd.size() != 0) {
            int a = rd.pollFirst(), b = dd.pollFirst();
            if (a < b) rd.addLast(a + n);
            else dd.addLast(b + n);
        }
        return rd.size() != 0 ? "Radiant" : "Dire";
    }
}

C++ 代码：

class Solution {
public:
    string predictPartyVictory(string s) {
        deque<int> rd, dd;
        int n = s.length();
        for (int i = 0; i < n; i++) {
            if (s[i] == 'R') rd.push_back(i);
            else dd.push_back(i);
        }
        while (!rd.empty() && !dd.empty()) {
            int a = rd.front(), b = dd.front();
            rd.pop_front();
            dd.pop_front();
            if (a < b) rd.push_back(a + n);
            else dd.push_back(b + n);
        }
        return !rd.empty() ? "Radiant" : "Dire";
    }
};

Python 代码：

from collections import deque

class Solution:
    def predictPartyVictory(self, s: str) -> str:
        rd, dd = deque(), deque()
        n = len(s)
        for i in range(n):
            if s[i] == 'R':
                rd.append(i)
            else:
                dd.append(i)
        while rd and dd:
            a, b = rd.popleft(), dd.popleft()
            if a < b:
                rd.append(a + n)
            else:
                dd.append(b + n)
        return "Radiant" if rd else "Dire"

TypeScript 代码：

function predictPartyVictory(s: string): string {
    let rd: Array<number> = [], dd: Array<number> = [];
    let n: number = s.length;
    for (let i = 0; i < n; i++) {
        if (s.charAt(i) == 'R') rd.push(i);
        else dd.push(i);
    }
    while (rd.length != 0 && dd.length != 0) {
        let a: number = rd.shift()!, b: number = dd.shift()!;
        if (a < b) rd.push(a + n);
        else dd.push(b + n);
    }
    return rd.length != 0 ? "Radiant" : "Dire";  
};