什么是Heap?
Heap是一种满足堆属性的专用基于树的数据结构。在一个堆中,对于任何给定节点(除了根节点),该节点的值始终根据其父节点排序。

这种排序可以是以下两种类型:
- **最大堆:**在最大堆中,对于除根节点外的每个节点,节点的值最多等于其父节点的值。这意味着最大的元素位于根节点,随着向下遍历树,元素变得更小。简单来说,所有子节点都必须小于其父节点。
- **最小堆:**在最小堆中,对于除根节点外的每个节点,节点的值至少等于其父节点的值。这意味着最小的元素位于根节点,随着向下遍历树,元素变得更大。
堆的特点
堆还是一颗完全二叉树,这意味着树的所有层级都是完全填充的,如果最后一层不完整,节点会从左到右填充。
优先队列经常使用二叉堆实现,尽管这不是实现的唯一方式。当我们希望根据某些优先级值对队列进行排序时,它用于排序队列。
这意味着每个元素都有一定的优先级。元素的优先级决定了元素从优先队列中删除的顺序。
堆的实现
实现堆最简单的方法是不使用二叉树,而是使用一个数组数据结构。这是因为它们是完全二叉树。
通过使用数组,我们还确保树中没有间隙(除了最后一层必须从左到右填充),允许一种紧凑的表示,而不会浪费任何空间。
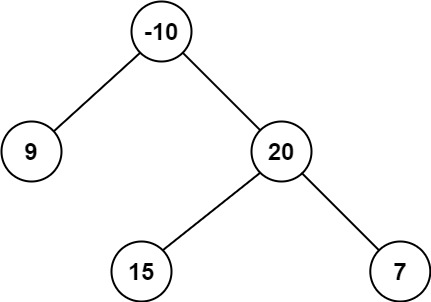
如果你仔细观察这个二叉堆,你会注意到每个节点下面都有一个索引,表示它在数组表示中的索引。
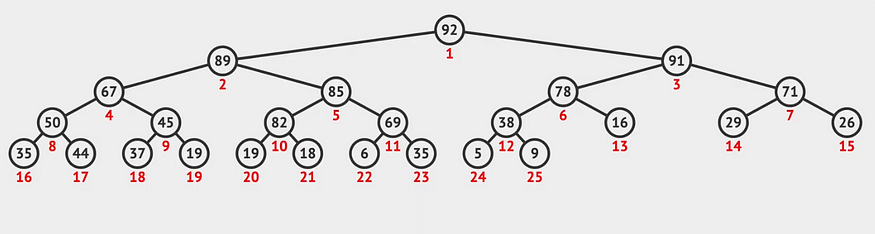
如果我们切换到数组视图,这就是我们的二叉堆的样子:

我们使用基于1的索引,这意味着我们不计算数组中的第0个项,根节点开始于索引1。在这种情况下,如果一个节点在数组中的索引为 i:
- 如果左子节点存在,则其索引为2*i。
- 如果右子节点存在,则其索引为2*i+1。
- 如果其父节点存在且
i不是1(根节点),则其父节点索引为 ⌊i/2⌋。
这意味着根节点从 arr[1] 开始,左节点是 arr[2],右节点是 arr[3] 等等。
这种表示利用了完全二叉树的属性,允许在不需要基于指针/引用的树节点结构之间轻松导航到父节点和子节点。
堆操作
堆的主要操作包括插入元素,提取最大/最小元素以及堆化以维护堆属性。
我建议查看这些操作的可视化表示以更好地理解它们。
插入
class Heap { constructor() { // 在这里使用 null 初始化堆以使用基于1的索引this.heap = [null]; } // 将新值插入堆中 insert(value) { this.heap.push(value); this.heapifyUp(this.heap.length - 1); } // 在插入后堆化以维护堆属性 heapifyUp(index) { while (index