目录
- 一、说明
- 二、球形 CNN概述
- 三、球面数据的对称性
- 四、标准(平面)CNN的局限性
- 五、卷积并发症
- 六、球面卷积
- 七、球面卷积是不够的

一、说明
球面数据的几何深度学习–球形 CNN。通过对物理世界的平移对称性进行编码,卷积神经网络 (CNN) 彻底改变了计算机视觉。
二、球形 CNN概述
在这篇博文中,我们研究了如何将CNN成功的基本原理转移到数据表现出复杂几何形状的问题范围,例如球体。
这篇博文由来自 Kagenova 的 Oliver Cobb 和 Augustine Mavor-Parker 共同撰写。
球面数据示例。[照片由 NASA 在 Unsplash 上拍摄]
T在过去十年中,CNN从传统(平面)图像和视频中提取语义意义的能力得到了迅速提高。如果有足够的数据,通常可以达到人类水平的性能。然而,对具有空间结构的数据进行分析远未解决问题。对于各种问题,数据表现出空间结构,但非平面结构。示例包括虚拟现实中的 360° 图像、来自宇宙大爆炸的宇宙微波背景 (CMB) 辐射、医学成像中的 3D 扫描以及计算机图形学中的网格表面,仅举几例。
对于这些问题中的每一个,我们都希望利用我们对数据结构的了解,特别是它们所遵循的对称性变换。正如在之前的博客文章中所讨论的,将对称性的理解编码到机器学习模型中可以成为限制所考虑模型空间的有效方法,从而可以更有效地学习模型。
对于平面上的图像,通过应用一堆卷积滤波器,可以在图像上平移,从而轻松有效地对平移对称性进行编码。由于在所有位置都应用了相同的卷积滤波器,因此结果操作是平移等变的,即它尊重平移对称性。这意味着无论特征位于图像中的哪个位置,它都会以相同的方式刺激相应位置的激活神经元。
不幸的是,对于非平面结构的问题,通常不存在这种简单的程序来编码对起作用的对称性的理解。然而,对于这些问题,新兴的几何深度学习领域的研究人员正在制定新的方法,这些方法利用了数据几何形式的属性,并尊重了起作用的对称性。最近取得重大进展的一系列问题是那些在球体表面上定义数据的问题。
三、球面数据的对称性
许多字段都涉及固存在于球体上的数据。
在球面上的每个点进行观测时,例如地球的地形图,可能会产生球面数据。然而,当对方向进行观测时,例如宇宙学中的宇宙微波背景 (CMB) 或虚拟现实和计算机视觉中的 360° 图像(见下图),也会出现这种情况。在Kagenova,我们正在努力解决深度学习在这些问题和其他涉及复杂几何数据(如球体)方面取得的巨大成功。

Examples of spherical data. [Original figure created by authors.]
对于平面图像,CNN 规定定义特定特征如何变换的规则不应依赖于特征恰好位于平面中的位置。对于在球体上定义的数据,我们希望规定规则不应取决于要素在球体上的方向和位置。变换特征,然后旋转其变换形式应等同于旋转特征并变换其旋转形式。关于此属性的操作被称为旋转等变的(见下图)。
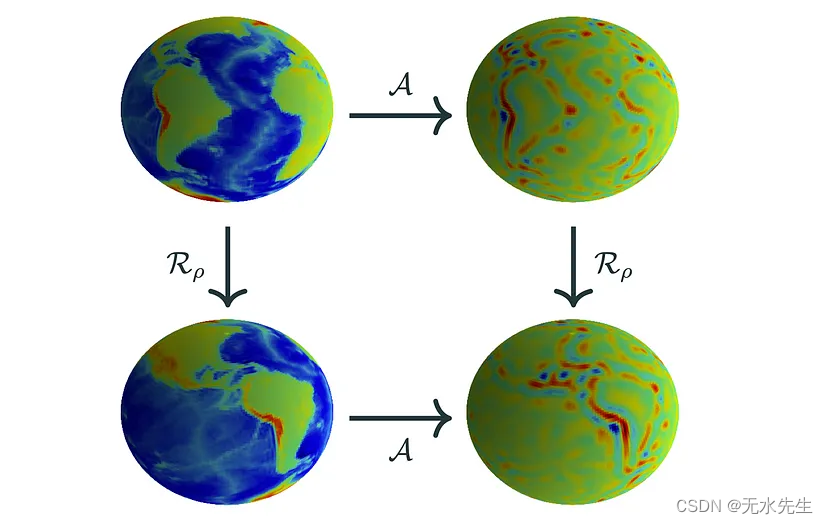
旋转等方差的图示。给定球面数据(左上),应用变换 (A) 获得特征图(右上),然后旋转 (Rρ) 特征图(右下)等效于先旋转数据(左下)然后应用变换(右下)。[作者创作的原始数字。]
在物理学中,规定控制系统行为的物理定律不应取决于系统的方向,从而产生了角动量守恒定律。因此,毫不奇怪,量子物理学中用于研究角动量的一些相同机制可用于定义深度学习中的旋转等变层(我们将在后面看到)。
四、标准(平面)CNN的局限性
在深入研究球形深度学习的想法之前,也许很自然地想知道为什么不能直接利用平面 CNN 的有效性。我们能不能不能将球面数据投射到某个平面表示上,而简单地以通常的方式应用CNN?毕竟,我们熟悉球形世界的平面投影(地图)。
投影的问题在于,不存在从球体到平面的投影,它同时保留了形状和面积。换句话说,扭曲是不可避免的。
这就是为什么格陵兰岛在地球地图上通常看起来与非洲相似,而实际上它的大小不到非洲的十分之一(见下图)。
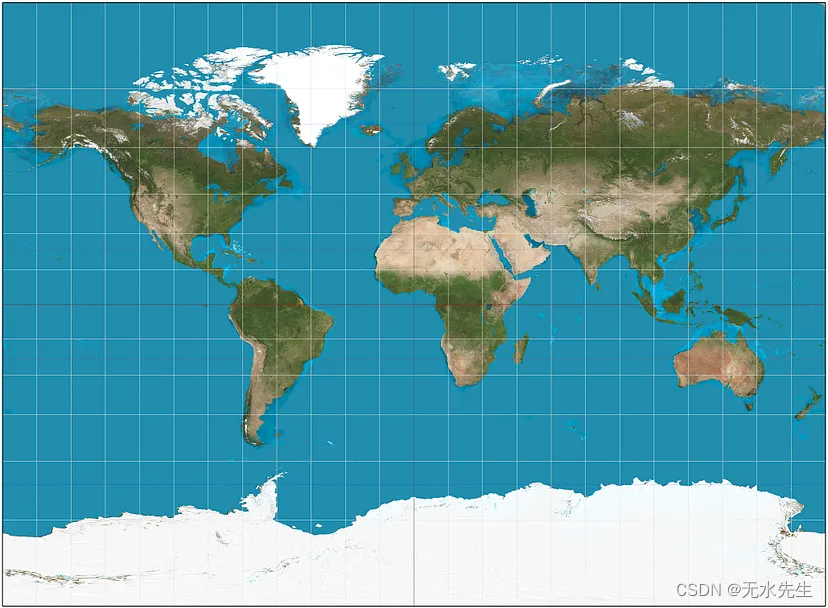
球体到平面的投影会引入不可避免的变形,与所使用的投影方法无关。出于这个原因,格陵兰岛在地球地图上通常看起来与非洲相似,但实际上还不到非洲的十分之一。[图片来自Wikimedia Commons。
这些失真意味着,当将传统CNN应用于球形图像的平面投影时,特征的显示方式会根据它们所在的位置而有所不同。当应用于球面图像的平面投影时,平面 CNN 的平移等方差不会编码旋转等方差。编码旋转等方差需要一个专门为球体几何形状设计的卷积概念。
五、卷积并发症
不幸的是,平面 CNN 实现的简单卷积过程不能应用于球形设置。
要了解为什么会这样,首先考虑平面数据的形式。平面数据表示为像素值的 2D 数组。对于在平面上定义的数据,我们可以在水平和垂直方向上均匀地划分像素位置。平面的这种统一采样意味着每个像素都有关联的邻居,并且所有像素的邻居位于相同的相对位置(北、东北、东等)。这意味着,通过平移,在相同采样位置定义的任何滤波器都可以以输入中的任何像素为中心,从而使样本完全对齐。
不幸的是,没有办法对球体进行采样,使所有像素的邻居都处于相同的相对位置。球体上的位置通常使用球面坐标来描述,θ 测量极角,φ测量方位角。相对于 θ 和 φ 均匀间隔样品可得到下图左侧所示的球体采样。如果我们使用这些采样位置来定义过滤器,然后旋转过滤器,我们会发现样本位置不对齐(见下图)。无论我们如何选择对球体进行采样,这都是正确的。

假设我们使用与球面数据相同的样本位置来定义一个过滤器。这样就不可能评估滤波器在各种旋转下与数据的匹配程度,因为样本不对齐。对于球体的所有采样都是如此。[原创图由作者创作。
众所周知,不可能以不变于旋转的方式离散球体。因此,不可能构造一个严格旋转等变的纯离散球面卷积。
为了构造一个捕捉旋转等方差所需性质的卷积球形概念,我们必须考虑连续表示。值得庆幸的是,存在这样一种表示,可以执行自然的卷积概念。
考虑球体上连续信号的表示。这些是函数 f:S² → R,将值与球体 S² 上的每个点 (θ, φ) 相关联,而不仅仅是在选定的样品位置。正如圆上的连续信号(即周期函数)可以分解为正弦和余弦函数的加权和一样,球面上的连续信号也可以类似地分解为谐波基信号的加权和(见下图)。在这两种情况下,都可以使用权重(系数)来表示信号,从而产生圆上信号的傅里叶级数表示和球面上信号的球谐表示。
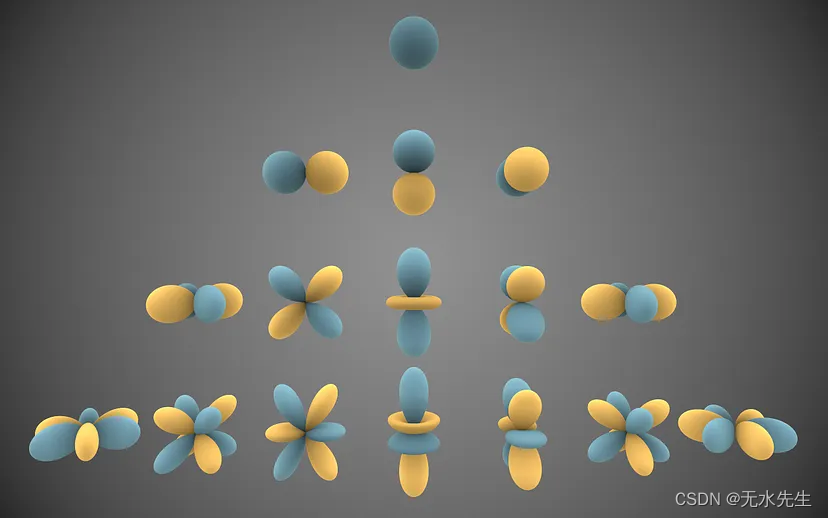
球谐波函数。[图片来自Wikimedia Commons。
尽管这种表示是无限的,但通过适当地截断系数向量,可以非常准确地近似真实世界的信号。从上图中我们可以看到,低度球谐波只能捕获低频变化,而高度球谐波可以捕获较高频率的变化。我们截断的点决定了数据表示的分辨率。
六、球面卷积
回想一下,我们想对满足旋转等方差性质的球面数据进行变换。
有一个非常自然的球面卷积概念,在连续设置中类似于在平面情况下执行的卷积。
这是取球面信号 f:S² → R,定义一个球面滤波器 g:S² → R,并计算由
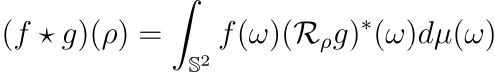
这里我们使用了旋转算子 Rρ,定义为 (Rρ g)(ω)=g(ρ⁻¹ω)。换句话说,它具有将相应的反向旋转应用于函数域的效果,类似于我们如何看待平移在一维线或二维平面上定义的函数。
上述等式的解释是,卷积信号 f * g 捕获了在任何给定旋转 ρ 下滤波器 g 与信号 f 的匹配程度(见下图)。这类似于平面情况,在平面情况下,我们考虑滤波器在各种转换下与输入的匹配程度。

使用滤波器(中)可视化数据的球面卷积(左)以生成特征图(右)。[原创图由作者创作。
这里的主要区别在于,定义卷积信号的空间,即旋转的空间(3D 空间),与定义卷积信号和滤波器的空间(2D 球体)不同。在上面所示的说明性示例中,滤波器不变于方位角旋转,因此输出保持在球体上。
然而,将输入信号从球体提升到 3D 旋转空间并不是特别成问题。随后可以在旋转空间上定义的信号和滤波器之间执行类似的卷积概念。因此,给定一个球面输入,为了分层学习特征,我们可以执行一个球面卷积,从而在 3D 旋转组上生成激活图,然后根据需要进行任意数量的旋转组卷积。
要了解为什么上述卷积概念是旋转等变的,请注意,将输入旋转 ρ 等同于对积分内部的滤波器施加额外的 ρ⁻¹ 旋转。反过来,这又具有旋转由 ρ⁻¹ 定义卷积信号的域的效果。换句话说,在执行卷积之前旋转输入等同于执行卷积,然后旋转输出。
两个球面信号的卷积似乎需要为三维空间中的每个值计算一个二维积分。然而,幸运的是,f * g 的谐波表示与 f 和 g 的谐波表示之间的关系很简单。球面卷积可以通过在 f 的谐波系数和 g 的谐波系数之间进行矩阵乘法来计算谐波空间。鉴于深度学习从业者习惯于利用 GPU 有效地执行矩阵乘法,这特别方便。
七、球面卷积是不够的
配备了可以有效实现的旋转等变线性操作,我们似乎拥有重复应用此操作并分层学习特征所需的一切。
然而,到目前为止,我们忽略了一个重要的组成部分——非线性的引入。
在平面网络中,非线性是由逐点激活函数引入的,即通过将选定的非线性函数分别应用于每个样本位置的值。由于平面采样方案的均匀性,这确实是一种平移等变操作。但是,我们已经过渡到使用没有关联样本位置或值的谐波表示。尽管可以获得基于样本的表示,但我们无法均匀地对球体进行采样(如上所述),这意味着对每个样本应用相同的非线性函数并不是严格意义上的旋转等变操作。
然而,以这种方式引入非线性是可能的,并且正如Cohen等人(2018)和Esteves等人(2018)所表明的那样,通常相当有效。然而,为了执行卷积和非线性运算,在谐波和基于样本的表示之间反复转换是很麻烦的。此外,人们很自然地想知道失去的等价方差在多大程度上阻碍了性能。
在我们的下一篇文章中,我们将看到如何利用量子物理学的思想直接在谐波空间中引入非线性,而不会影响我们对旋转对称性的尊重程度。
引用
[1] Cohen,Geiger,Koehler,Welling,球形CNNs,ICLR(2018),arxiv:1801.10130。
[2] Esteves、Allen-Blanchette、Makadia、Daniilidis,使用球形 CNN 学习 SO(3) 等变表示,ECCV (2018),arXiv:1711.06721。