(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛（6）-编程知识

1001 Count

当k在区间(1+n)/2的左边时,如图,[1,k]和[n-k+1,n]完全相同,所以就m^(n-k)

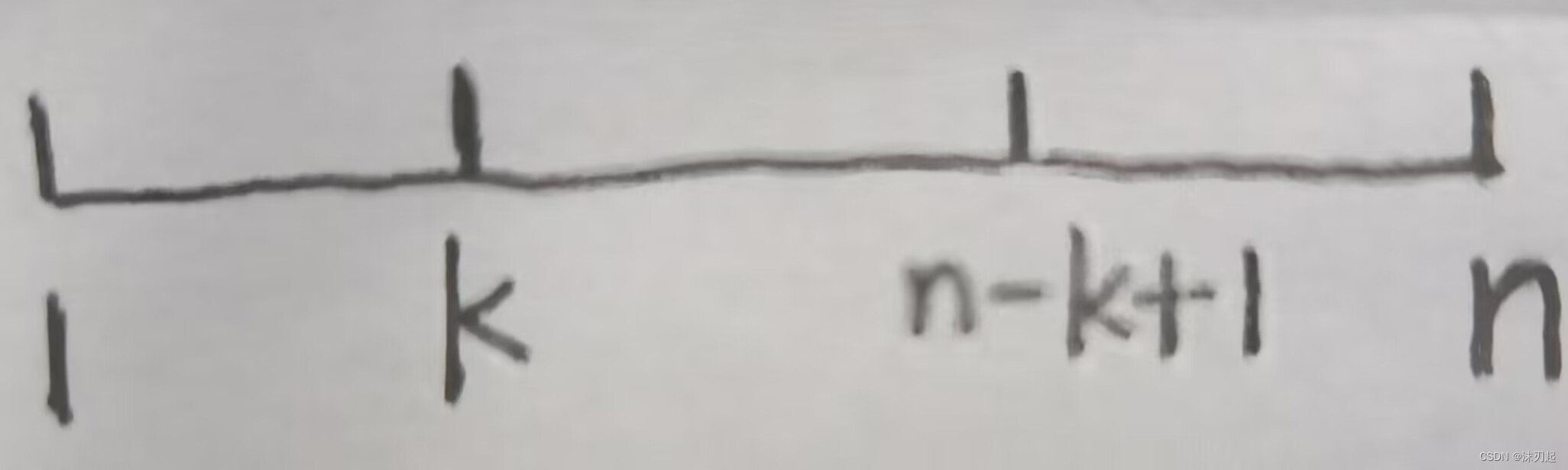
当k在区间(1+n)/2的右边时,如图,[1,n-k+1]和[k,n]完全相同,所以也是m^(n-k)

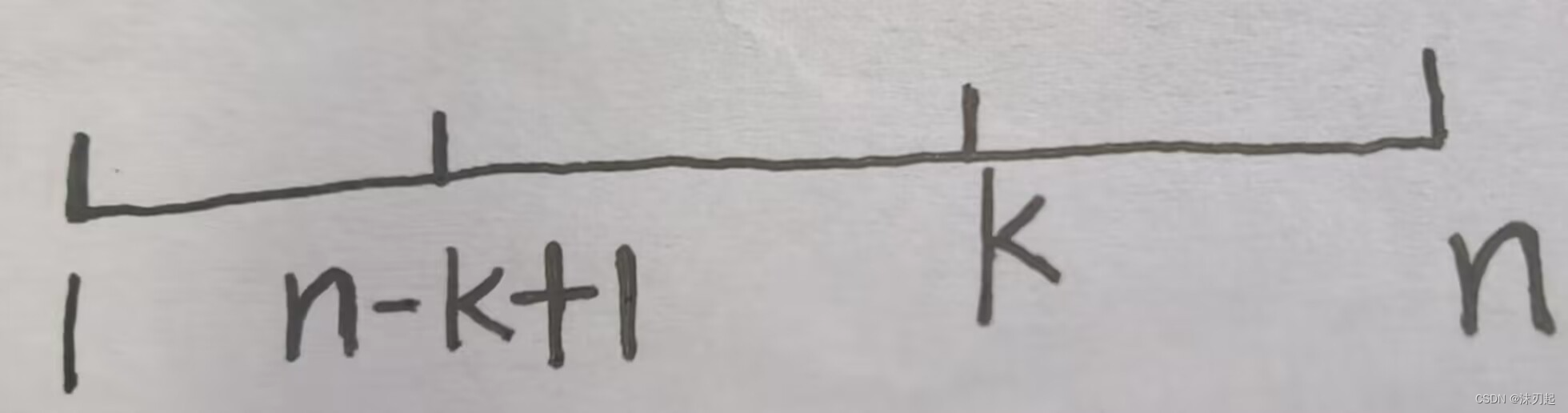
别忘了特判,当k等于n时,n-k为0,然后a1=a1,a2=a2,..an=an,所以没什么限制,那么就是m^n

AC代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int mod=998244353;
ll n,m,k;
ll qmi(ll a,ll k){ll res=1;while(k){if(k&1) res=res*a%mod;a=a*a%mod;k>>=1;}return res;
}
void solve() {cin>>n>>m>>k;ll res;if(n==k) res=qmi(m%mod,n)%mod;//m范围过大,可达1e18,取个模防止快速幂时爆long longelse res=qmi(m%mod,n-k)%mod;//m可以取模是因为快速幂本就是乘法运算,乘法运算完全可以一边运算一边取模cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}

参考2023杭电暑假多校6 题解 1 2 6 10 | JorbanS_JorbanS的博客-CSDN博客

1002 Pair Sum and Perfect Square

树状数组

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e5+10,M=450;
int p[N],pos[N];
int tr[N];
int sqr[M];
int n,q;
//树状数组
int lowbit(int x){return x & -x;
}
int sum(int x){int res=0;for(int i=x;i;i-=lowbit(i)) res+=tr[i];return res;
}
void add(int x,int c){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
void solve() {cin>>n;memset(tr,0,sizeof tr);for(int i=1;i<=n;i++) cin>>p[i],pos[p[i]]=i;//pos记录值为p[i]的下标int m=0;for(int i=1;i*i<=2*n-1;i++) sqr[m++]=i*i;//将所有可能用到的平方数从小到大全部都记录在sqr数组中cin>>q;vector<vector<PII>>s(n+1);for(int i=0;i<q;i++){int l,r;cin>>l>>r;s[r].push_back({i,l});//右端点为r,然后将第几次询问的编号以及左端点放进去}int res=0;vector<int>ans(q+1);//枚举i从1到n,i作为右端点的编号for(int i=1;i<=n;i++){//从小到大枚举所有平方数,j为编号,sqr[j]即为平方数for(int j=0;j<m;j++){if(p[i]>=sqr[j]) continue;//如果p[i]已经大于等于该平方数了,那么说明该平方数太小了,那么就continue,继续枚举下一个平方数if(sqr[j]-p[i]>n) break;//sqr[j]即为平方数,p[i]即为右端点i的所对应的值,sqr[j]-p[i]即为左端点对应的值,如果大于n,说明该平方数太大了,那么直接break,后面平方数更大，就不用枚举了if(pos[sqr[j]-p[i]]<i) add(pos[sqr[j]-p[i]],1),res++;//如果左端点的下标小于右端点的下标i,那么就是可行的,那么以pos[sqr[j]-p[i]]为左端点的位置上个数+1,res记录有几对可行}//以i为右端点,枚举每一次询问的编号,以及询问区间[l,i],每一次遍历到的编号都是唯一的,res表示枚举到当前所有满足条件的对数,用res减去sum(l-1)算出的就是[l,i]区间里面所有满足条件的对数//首先右端点i是从小到大依次枚举的,然后前面的枚举过的右端点肯定是在i前面的,然后我们需要保证左端点要大于等于l,所以减去sum(l-1)即左端点小于等于l-1的满足条件的对数for(auto [id,l]:s[i]) ans[id]=res-sum(l-1);}for(int i=0;i<q;i++) cout<<ans[i]<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}

1006 Perfect square number

法一：

将a[x]修改后区间和为平方数的个数=改之前区间和为平方数的个数-改之前含有x的区间和为平方数的区间个数+改之后含有x的区间和为平方数的区间个数

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N=310;
int a[N],s[N];
int n;
//判断x是否是平方数
bool check(int x) {if(pow((int)sqrt(x),2)==x) return true;return false;
}
void solve() {cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];s[i]=s[i-1]+a[i];//前缀和}int res=0;int ans=0;//不重不漏地枚举区间for(int i=1; i<=n; i++) {for(int j=1; j<=i; j++) {if(check(s[i]-s[j-1])) ans++;//ans记录一共有几个区间的区间和为平方数,即记录修改前的个数}}res=ans;for(int x=1; x<=n; x++) {int suml=0;int sum=0;//记录含有x的区间和为平方数的区间个数int cnt[90000]= {0};for(int i=x; i>=1; i--) {suml+=a[i];int sumr=0;for(int j=x; j<=n; j++) {sumr+=a[j];int sumn=suml+sumr-2*a[x];//把x删掉后含有x的区间的区间和为sumnif(check(sumn+a[x])) sum++;//如果含有x的区间和为平方数,那么sum++cnt[sumn]++;//记录去掉x后区间和为sumn的个数}}int f[400]= {0}; //f[i]记录将a[x]修改为i之后含有x的区间和为平方数的区间个数for(int i=1; i<=300; i++) {int m=i*i;//枚举所有的平方数//将a[x]修改为m-jfor(int j=m; j>=0&&m-j<=300; j--) {f[m-j]+=cnt[j];}}for(int i=1; i<=300; i++) {res=max(res,ans-sum+f[i]);}}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}

法二:

同样是将a[i]修改后区间和为平方数的个数=改之前区间和为平方数的个数-改之前含有i的区间和为平方数的区间个数+改之后含有i的区间和为平方数的区间个数

只不过预处理的方式不一样

算改之前区间和为平方数的个数-改之前含有x的区间和为平方数的区间个数:

通过算区间和为平方数的区间个数前缀和以及区间和为平方数的区间个数后缀和,用数组x记录前缀和,用数组y记录后缀和,比如说我们要修改a[i],那么只要将x[i-1]和y[i+1]加起来即可,这样算出来的就是和i无关的区间和为平方数的区间个数,也就是改之前区间和为平方数的个数-改之前含有i的区间和为平方数的区间个数

接下来就只需要算改之后含有i的区间和为平方数的区间个数

for (int j = i; j <= n; j ++) pre(i, j, 1);
for(int j=1; j<=i-1; j++) pre(j,i-1,-1);

着重解释以上两句,我们想的是假设我们要修改第i个数,那么我们枚举与i有关的所有区间,即[i,i],[i,i+1],....[i,n]

以及[1,i],[2,i],...[i-1,i],但是由于我们枚举前面的i时,已经算过了,会导致重复,所以我们只要每次加上以i为左端点的区间就行,例如:

当i为1时,我们枚举以1为左端点的所有区间就已经是与1有关的所有区间了,如图,[1,1],[1,2],[1,3],[1,4],[1,5]

然后我们枚举以2为左端点的所有区间,如图,[2,2],[2,3],[2,4],[2,5],实际上呢,我们仍要枚举以2为右端点的所有区间,我们发现前面已经枚举过了,但是呢,我发现多了[1,1]这个与2无关的区间,所以我们要减去与2无关的区间,即[1,1]

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N=610,M=300;
int a[N],s[N];
int x[N],y[N];
int f[N];
int n;
//判断x是否是平方数
bool check(int x) {if(pow((int)sqrt(x),2)==x) return true;return false;
}
void pre(int l, int r, int k) {int sum = s[r] - s[l - 1];//i代表变化值,如果将i修改后,与i有关的区间和为平方数,那么就用数组f记录变化值(加一个M,使得原来从-300到300映射为0到600)的个数for (int i = -M; i <= M; i ++)if (check(sum + i)) f[i + M] += k;
}
void solve() {memset(x,0,sizeof x);memset(y,0,sizeof y);memset(f,0,sizeof f);cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];s[i]=s[i-1]+a[i];//前缀和}//不重不漏地枚举区间for(int i=1; i<=n; i++) {for(int j=1; j<=i; j++) {if(check(s[i]-s[j-1])) x[i]++;//如果区间和为完全平方数,那么以i为右端点的区间和为平方数的区间个数+1}x[i]+=x[i-1];//跑一遍前缀和,数组x记录[1,i]中有多少个区间的区间和为平方数,即区间和为平方数的区间个数前缀和}for(int i=n; i>=1; i--) {for(int j=i; j<=n; j++) {if(check(s[j]-s[i-1])) y[i]++;//如果区间和为平方数,那么以i为左端点的区间和为平方数的区间个数+1}y[i]+=y[i+1];//跑一遍后缀和,数组y记录[i,n]中有多少个区间和为平方数,即区间和为平方数的区间个数后缀和}int res=0;for(int i=1; i<=n; i++) {for (int j = i; j <= n; j ++) pre(i, j, 1);for(int j=1; j<=i-1; j++) pre(j,i-1,-1);//以上两个循环是为了算修改第i个数后的与i有关的区间和为平方数的区间个数(假设f[关键字]=值,那么关键字放的是变化值的映射,值为个数)int now=0;for(int j=1; j<=M; j++) now=max(now,f[j-a[i]+M]);res=max(res,x[i-1]+y[i+1]+now);}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}

1010 Caclulate

倍增的思想:任何一个十进制数都可以表示为若干个2的次幂的和

手上初始的数字为y,到点i,数字变为ki*y+bi,从点i到点j,数字变为ki*kj*y+kj*bi+bj

所以我们可以先预处理从每一个点走很多很多步的y前面的系数以及b(形式为k*y+b,我们需要预处理k以及b),由于走的步数是十进制数,而且可以达到很大,因为任意一个十进制数都可以由若干个2的次幂的和组成,所以对于每一个点,我们直接预处理从该点每次走2的次幂,那么最多走2的几次幂呢?由于最大到1e9,所以最多走2的30次幂

AC代码:

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
const int mod=1e9+7;
const int N=1e5+10,M=31;
typedef long long ll;
int p[N][M];
ll k[N][M],b[N][M];
int n,q;
int query(){int x,l,y;cin>>x>>l>>y;x=p[x][0];//起点为x,先走一步//枚举2的次幂,比如4的二进制为100,然后和l进行与运算,如果l所对应的二进制的这一位也有1的话,那么该2的次幂就可以是l的一部分for(int i=0;i<M;i++){if((1<<i)&l){y=(y*k[x][i]+b[x][i])%mod;x=p[x][i];} }return y;
}
void solve() {cin>>n>>q;for(int i=1;i<=n;i++) cin>>k[i][0];for(int i=1;i<=n;i++) cin>>b[i][0];for(int i=1;i<=n;i++) cin>>p[i][0];for(int j=1;j<=30;j++){for(int i=1;i<=n;i++){p[i][j]=p[p[i][j-1]][j-1];//p[i][j]表示从位置i走2^j可以由位置i走2^(j-1)到达位置p[i][j-1],再从位置p[i][j-1]走2^(j-1)转移而来k[i][j]=k[i][j-1]*k[p[i][j-1]][j-1]%mod;//k[i][j]表示从点i开始包括i数4个数所对应的y前面的系数b[i][j]=(b[i][j-1]*k[p[i][j-1]][j-1]+b[p[i][j-1]][j-1])%mod;//b[i][j]同理,表示从点i开始包括i数4个数所对应的b}}while(q--) cout<<query()<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}