文章目录
- 前言
- 一、全加器是什么?
- 二、使用步骤
- 1.半加器
- 2.全加器
- 1.新建一个全加器工程
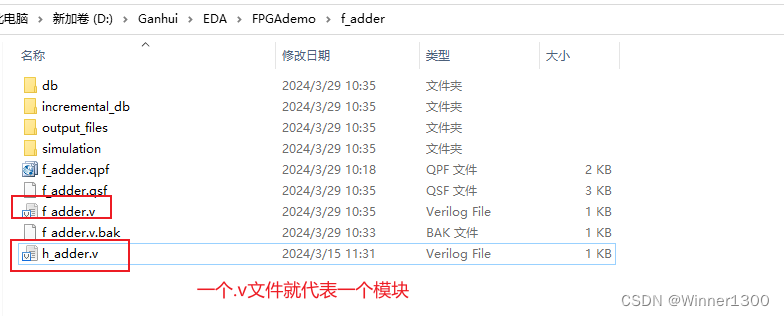
- 2.添加半加器的.v文件到全加器工程中
- 3.新建全加器.v文件,写程序,调用半加器.v文件 完成例化
- 三、仿真效果
- 总结
前言
提示:这里可以添加本文要记录的大概内容:
项目需要:
提示:以下是本篇文章正文内容,下面案例可供参考
一、全加器是什么?
示例:
二、使用步骤
1.半加器

代码如下(示例):
module h_adder(A,B,SO,CO);input A,B;
output SO,CO;assign SO= A^B;
assign CO= A&B;endmodule2.全加器
1.新建一个全加器工程
新建文件夹
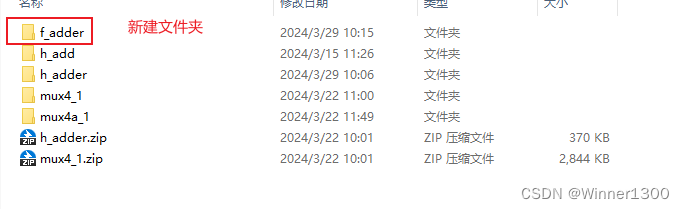
在文件夹内新建工程
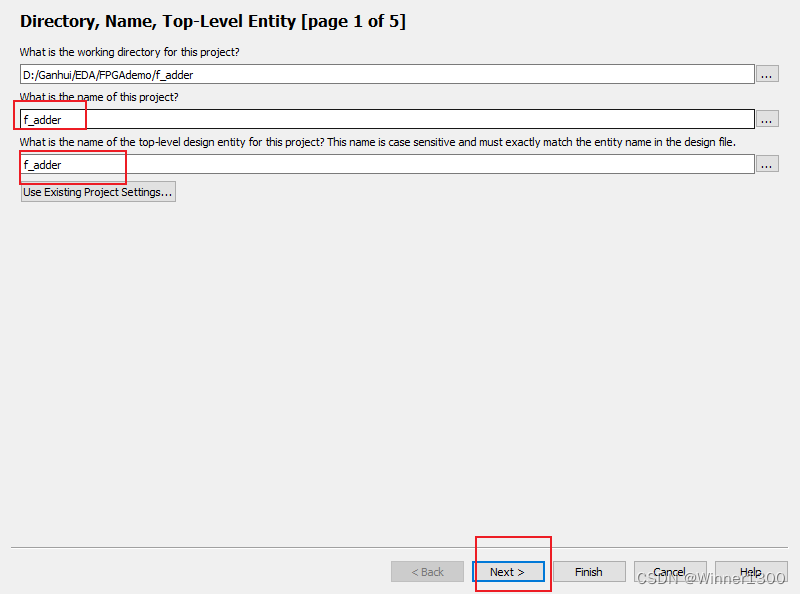
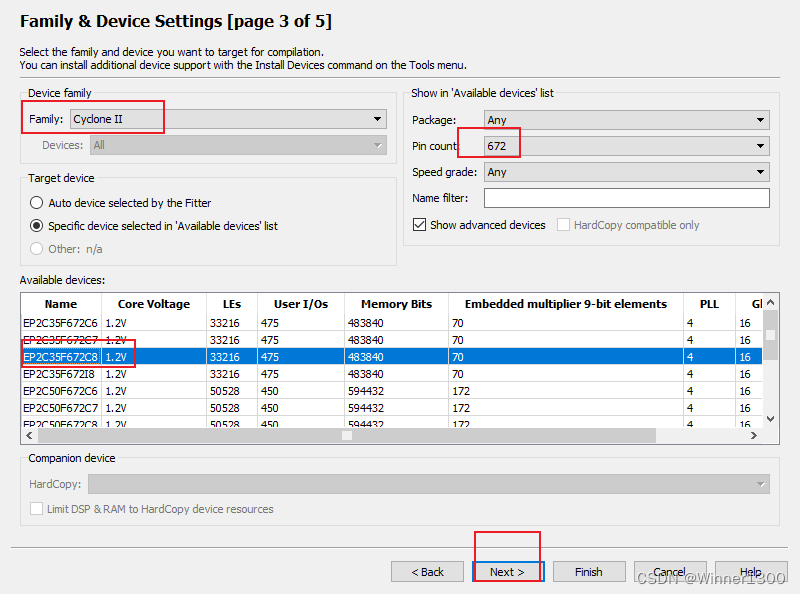
新建工程完毕
2.添加半加器的.v文件到全加器工程中
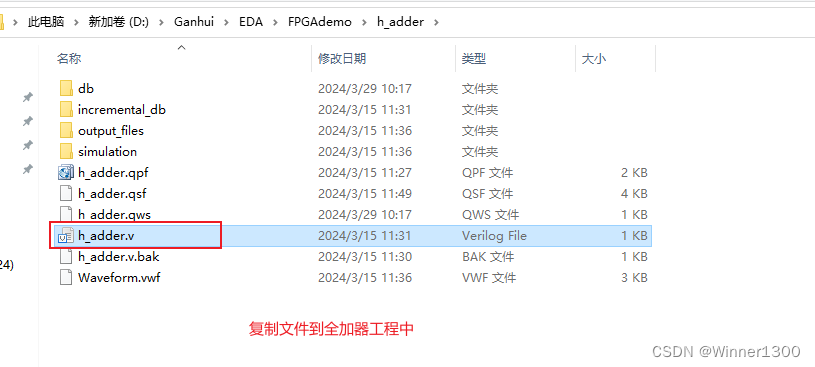
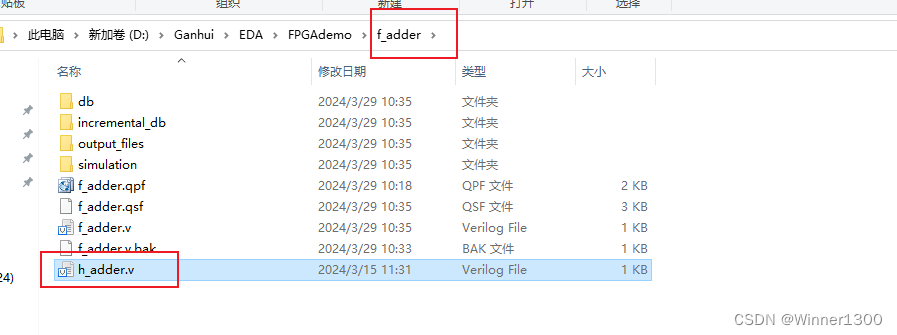
3.新建全加器.v文件,写程序,调用半加器.v文件 完成例化
代码如下(示例):
module f_adder(a,b,c,sum,so);input a,b,c;
output sum,so;wire net_sum;
wire net_co1;
wire net_co2;h_adder U1(a,b,net_sum,net_co1);
h_adder U2(.A(net_sum),.B(c),.SO(sum),.CO(net_co2));or U3(cout,net_co1,net_co2);endmodule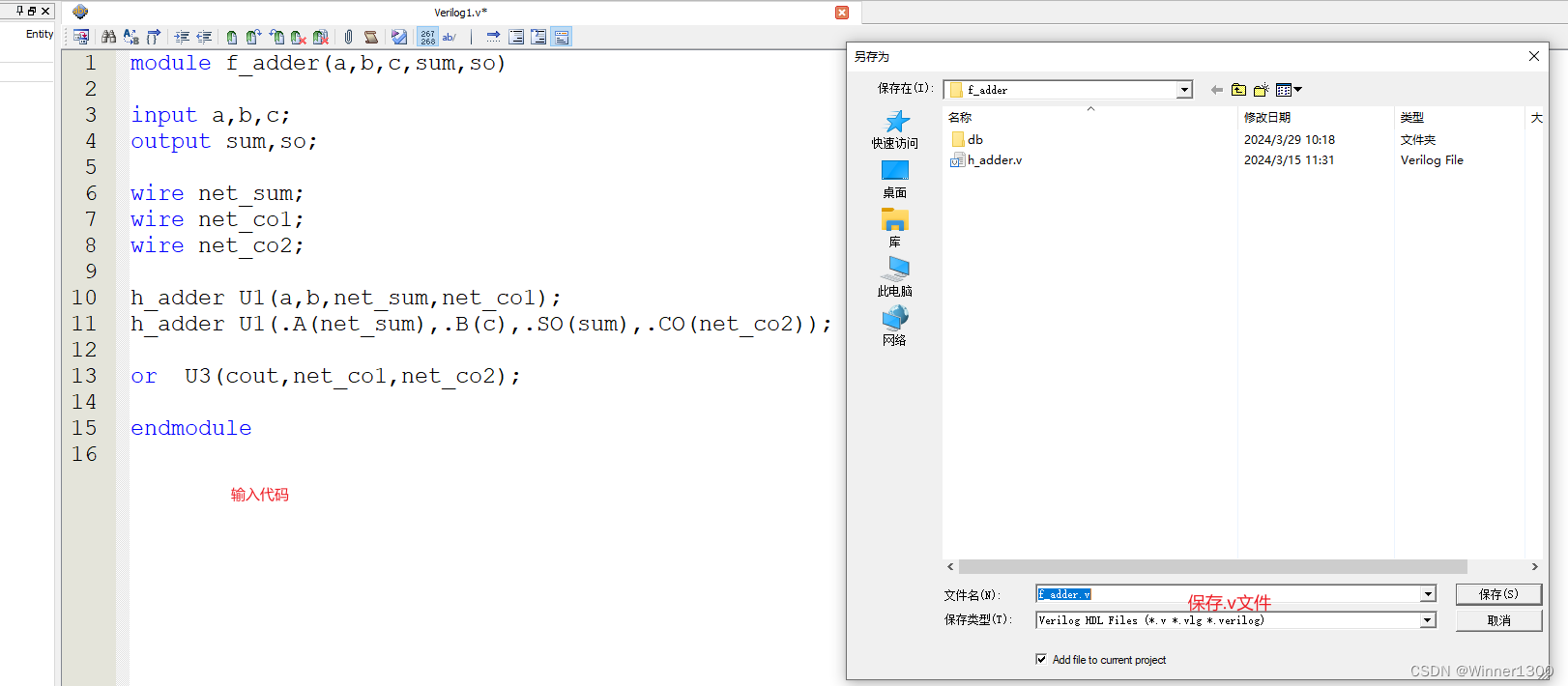
编译:
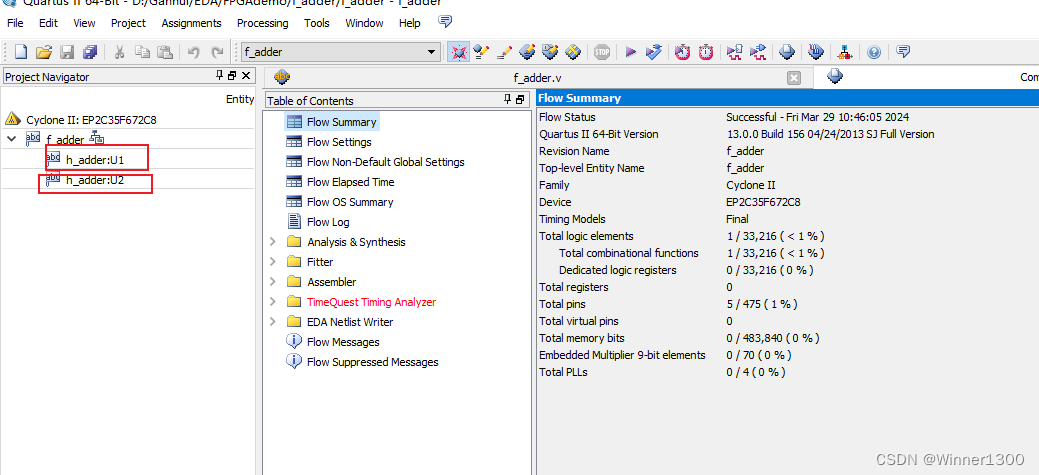
三、仿真效果
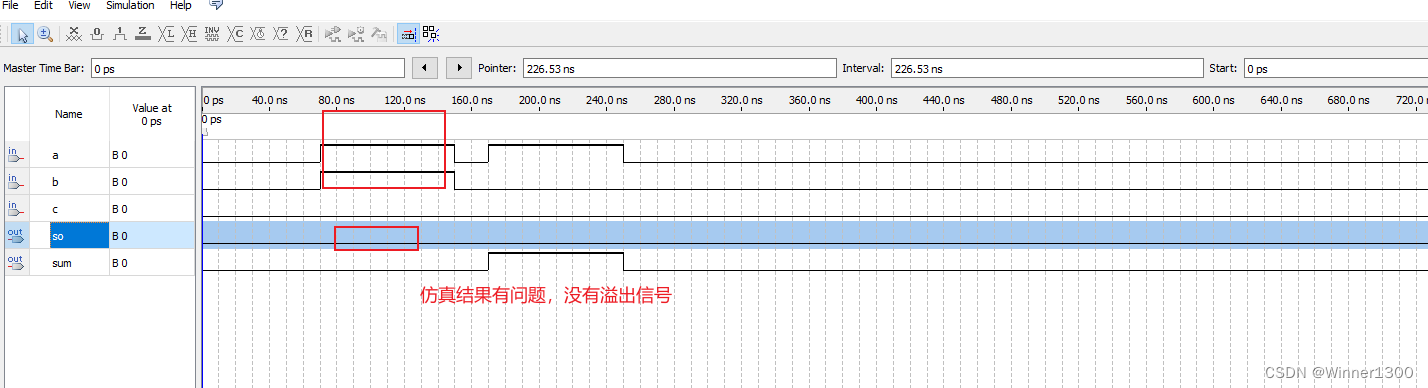
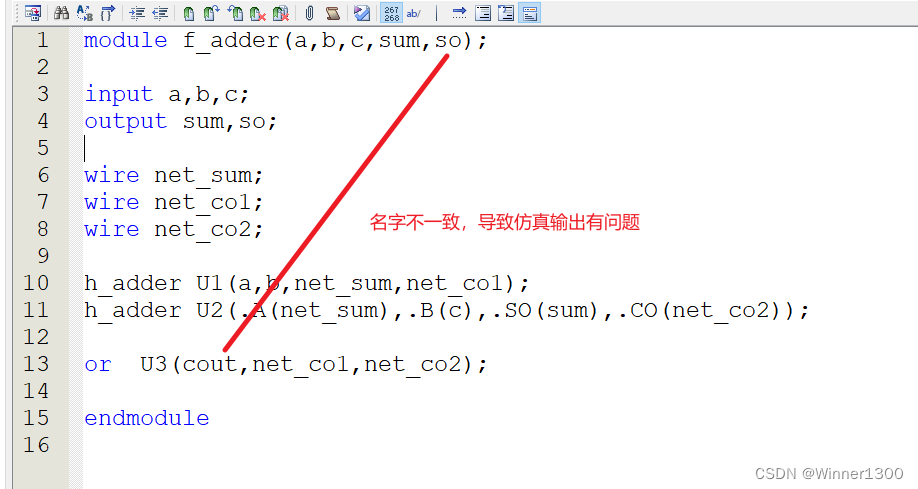
修改:
module f_adder(a,b,c,sum,co);input a,b,c;
output sum,co;wire net_sum;
wire net_co1;
wire net_co2;h_adder U1(a,b,net_sum,net_co1);
h_adder U2(.A(net_sum),.B(c),.SO(sum),.CO(net_co2));//or U3(so,net_co1,net_co2);
assign co=net_co1 |net_co2;endmodule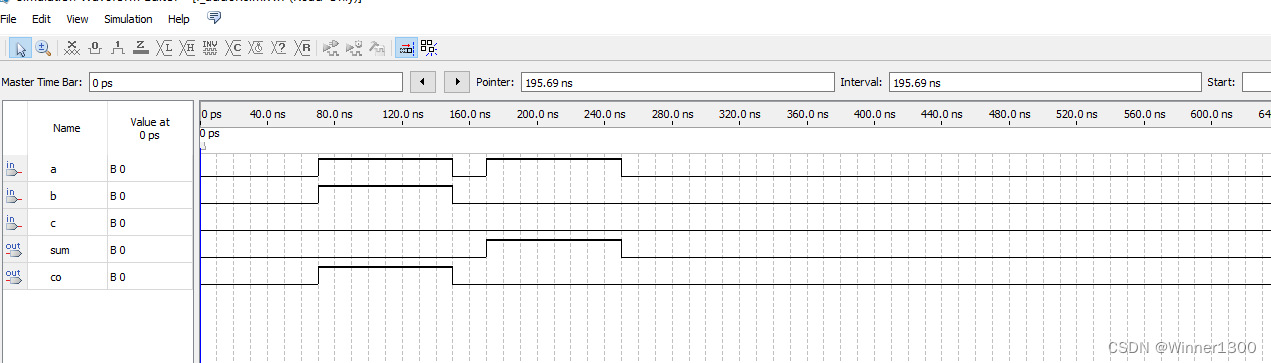
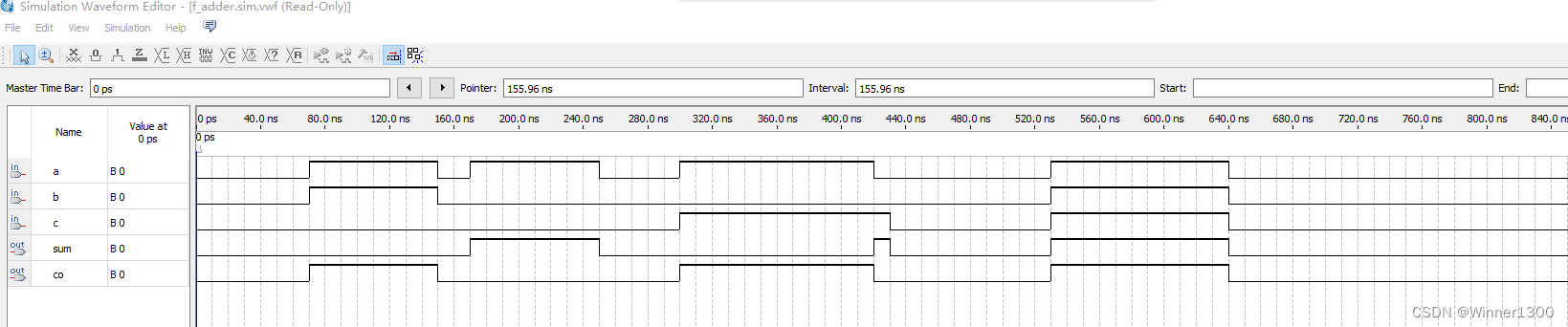
最后代码
module f_adder(a,b,c,sum,co);input a,b,c;
output sum,co;wire net_sum;
wire net_co1;
wire net_co2;h_adder U1(a,b,net_sum,net_co1);
h_adder U2(.A(net_sum),.B(c),.SO(sum),.CO(net_co2));or U3(co,net_co1,net_co2);
//assign co=net_co1 |net_co2;endmodule总结
重点例化语句的应用,为后面程序拓展增加了奠定了基础