文章目录
- 随机森林
- 决策树
- 基础
- 特征值问题?
- 聚类算法
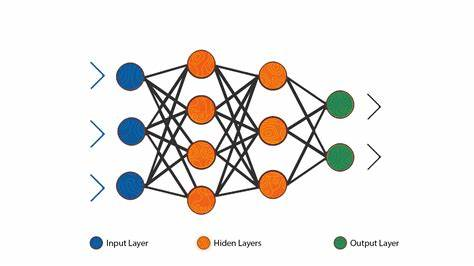
随机森林
决策树
基础
概念:从根节点一步步走到叶子节点(决策);
组成:根节点=第一个选择的节点;叶子节点=最终的决策结果;非叶子节点=中间过程;
训练:除叶子节点之外所有的特征节点,选择节点的过程以及构建树的过程;
测试:已知树的结构,输入数据,得到最终该数据要去哪个叶子节点;
如何选择特征:通过某种衡量标准,计算哪个特征作为根节点;衡量标准是熵;
熵值:表示随机变量的不确定性度量。公式如下:H(X)=-∑ pi* logpi, i=1,2,…n
概率是0-1之间的一个数,某类别概率越大,则logpi就越小,即给定数据中选择该类别对象,选中的概率越大。选不中的概率就越小(即熵值越小);
信息增益:表示特征X使得类Y的不确定性减少的程度。通过选取X作为节点,将所有数据分成两组,每组计算熵值,于初始熵值比较,若熵值减少值最大,则说明该特征X选取合适。
决策树方式:需要采用预训练的方式,即需要带标签的数据。
特征的衡量标准,除了熵值还有GINI系数。某类别概率越大,GINI系数越小。
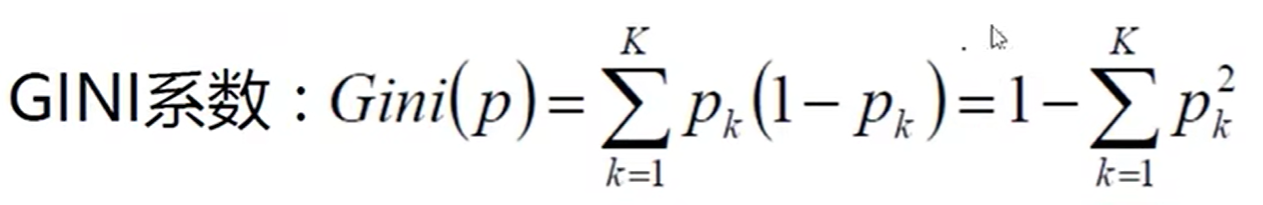
特征值问题?
特征有离散和连续,离散特征包含离散情况、类别变量;对于连续值应该如何判断?


![Vue element-plus 导航栏 [el-menu]](https://img-blog.csdnimg.cn/direct/cad688c77fb44593af301196dd40a963.png)