状态压缩dp[详解 + 例题]-编程知识

状态压缩dp[详解 + 例题]

1 . 题目

2 . 分析

可以发现 : 横放的方案数 == 总方案数 ;

剩下的都是竖放去填补空缺 ;

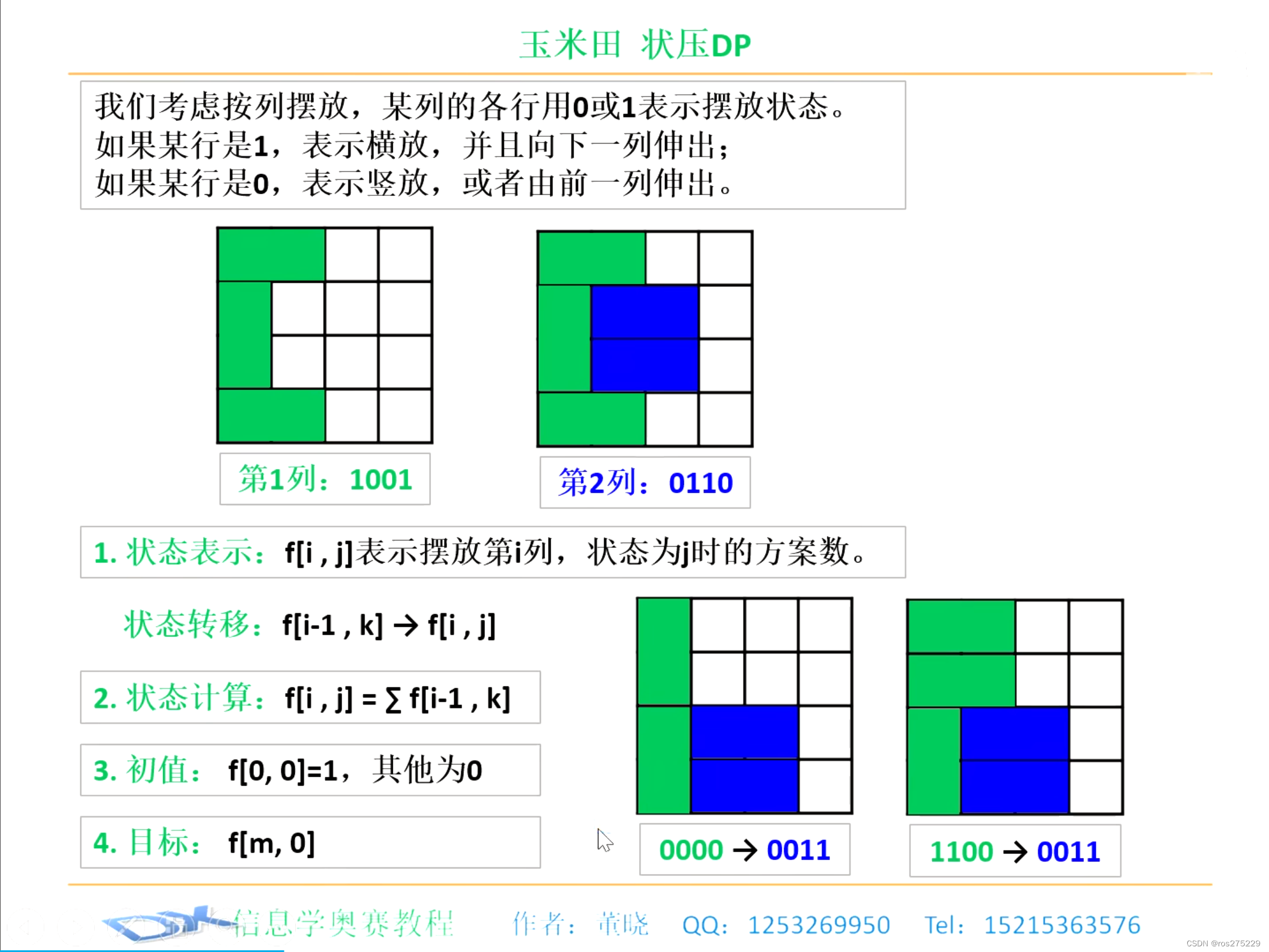
关于状态定义 :

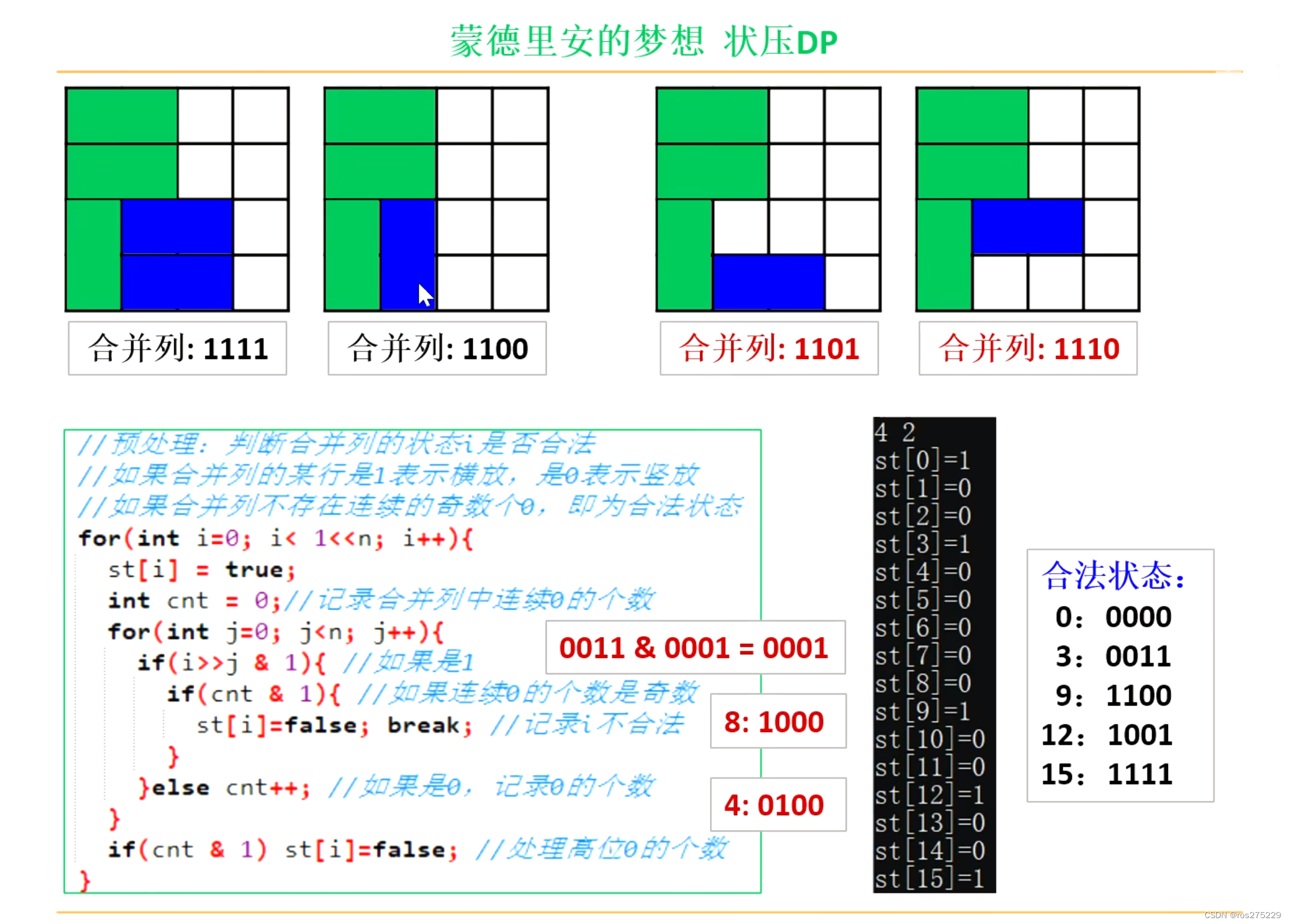
考虑按列拜访，某列的隔行用0/1表示摆放状态 ;

某行为1 : 表示横放 , 0 : 表示竖放 ;

状态表示 :

f[i][j] : 表示拜访第i列，状态为j的方案数 ;

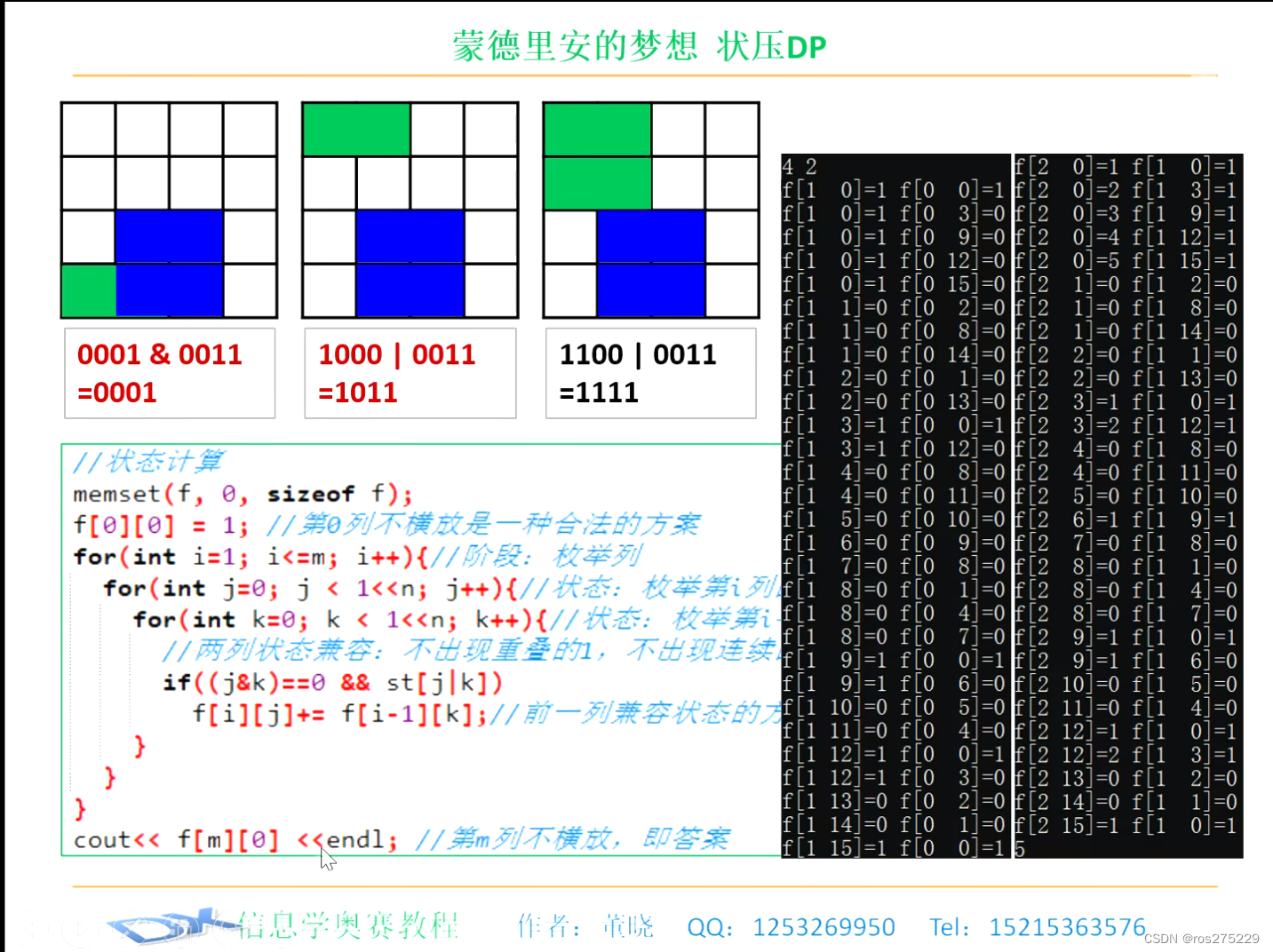
状态转移 :

f[i-1][k] --> f[i-1][j];

其中k表示i-1列并且能够与j匹配的状态 :

状态计算 :

f[i,j] = sum(f[i-1],k) ;

初值 :

f[0][0] = 1;

目标 :

f[m , 0]

3 . 代码 :

链接 :

291. 蒙德里安的梦想 - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int N =  110 ;
bool st13N];
int f[13][2050] ; 
int main(){int n , m ; while(cin >> n >> m ,m||n){// 预处理 : 判断合并列的状态i是否合法// 合并列1表示横放 ， 0表示竖放 // 如果合并列存在连续奇数个0,为非法状态，反之合法 // 比如n=4的时候,合法状态有0(0000),3(0011),9(1001),12(11010),15(1111) for(int i=0;i< 1<<n ;i++){ // 枚举到2^n-1,一共2^n个状态st[i] = true ;int cnt = 0 ; // 记录合并列中连续0的个数for(int j=0;j<n;j++){//从低位到高位移 if(i>>j & 1){ // 如果是1 if(cnt&1){st[i] = false ;break ;// 记录i不合法 }}else cnt ++ ;// 如果是0 , 记录0的个数 	} if(cnt & 1) st[i] = false ;//如0100,要判断高位0的情况 }// 状态计算 : memset(f , 0 , sizeof f) ;f[0][0] = 1 ;// 第0列不横放是一种合法的方案for(int i=1;i<=m;i++){// 阶段 : 枚举列 for(int j=0;j< 1<<n ;j++){ // 状态 : 枚举第i列的状态for(int k=0;k< 1<<n;k++){ // 枚举第i-1列的状态 // 不出现重叠的1,不出现连续的奇数个0if((j&k)==0 && st[j|k]){f[i][j] += f[i-1][k] ;// 前一列兼容状态的方案数之和 } } }} cout << f[m][0] << endl ;// 第m列，不横放，即答案 	}
}