分割回文串
力扣原题链接
问题描述
给定一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。
示例
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
解题思路
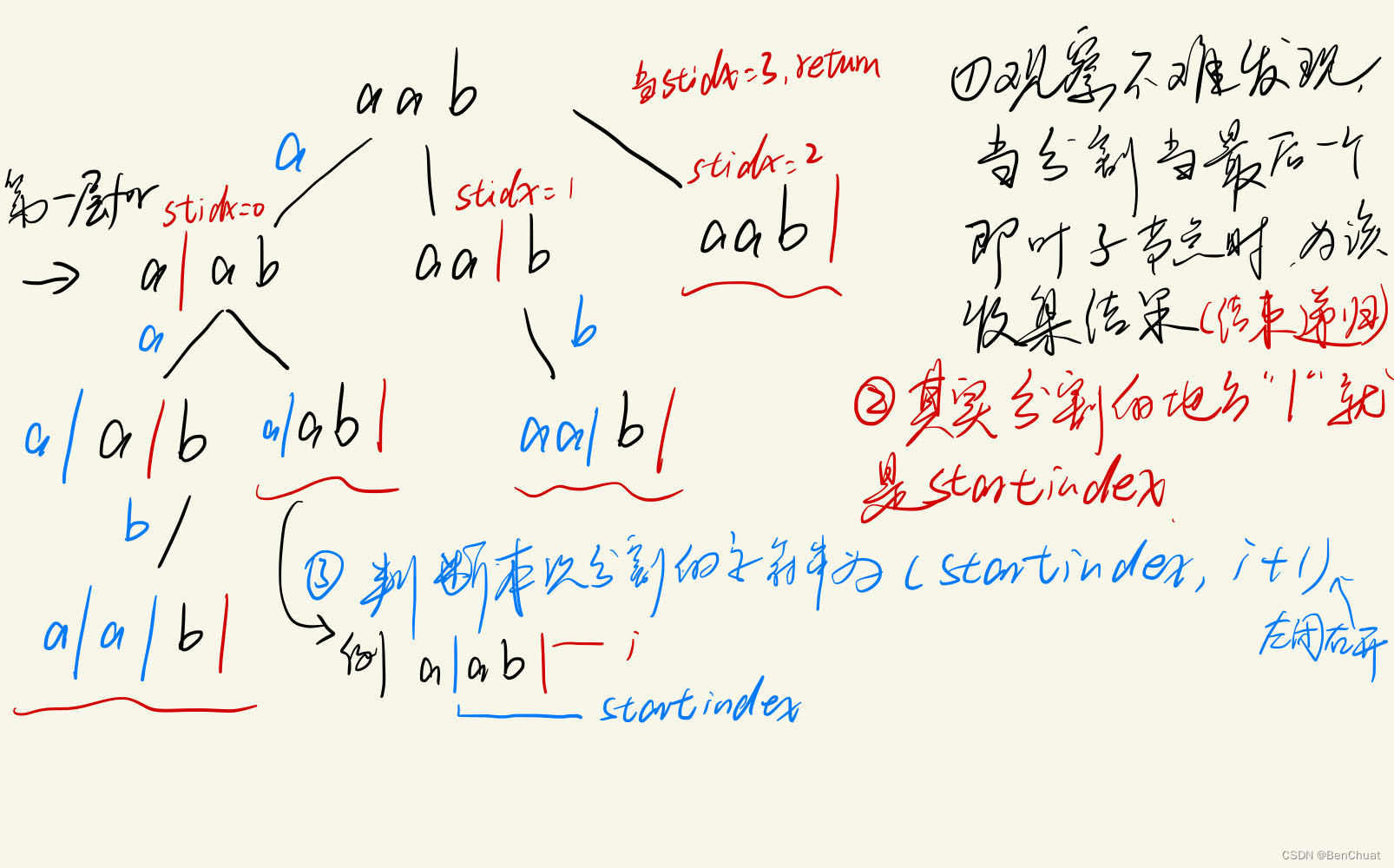
这是一个典型的回溯算法问题。我们需要从字符串的开头开始,逐步尝试切割出回文子串,并将这些回文子串组合成分割方案。
- 回溯搜索: 定义一个回溯函数
backtrack,其参数包括当前处理的索引start、当前的字符串s和当前的回文子串列表path。 - 结束条件: 如果当前索引
start等于字符串s的长度,说明已经处理完了整个字符串,将当前回文子串列表加入结果列表,并返回。 - 选择列表: 从当前索引
start开始的所有可能的回文子串。 - 遍历选择: 从当前索引
start开始,向后扫描字符串,依次尝试切割出回文子串。 - 判断回文: 对于每个可能的切割点,判断从当前索引
start到该切割点是否构成回文子串。 - 递归进入下一层: 如果切割点构成回文子串,则将该回文子串加入当前回文子串列表,并递归调用回溯函数,传入新的索引
i + 1、新的字符串s和更新后的回文子串列表。 - 撤销选择: 回溯到上一层时,将刚刚加入的回文子串从列表中删除,继续尝试下一个切割点。
Java解题
垃圾版
import java.util.*;class Solution {List<List<String>> res = new ArrayList<>(); // 存储结果的列表public List<List<String>> partition(String s) {List<String> path = new ArrayList<>(); // 存储当前回溯路径的列表backtrack(s, 0, path); // 调用回溯函数,从索引 0 开始遍历字符串 sreturn res; // 返回结果列表}// 回溯函数public void backtrack(String s, int start, List<String> path) {if (start == s.length()) { // 如果起始索引达到了字符串的长度,说明已经遍历完成res.add(new ArrayList<>(path)); // 将当前回溯路径添加到结果列表中return; // 返回结束当前回溯路径}for (int i = start; i < s.length(); i++) { // 遍历字符串 s,从当前起始索引开始String substr = s.substring(start, i + 1); // 获取当前子串if (isPalindrome(substr)) { // 如果子串为回文串path.add(substr); // 将回文子串添加到当前路径中backtrack(s, i + 1, path); // 递归进入下一层,从下一个字符开始遍历path.remove(path.size() - 1); // 回溯,撤销选择,将当前回文子串移出路径}}}// 判断字符串 s 是否为回文串public boolean isPalindrome(String s) {return s.equals(new StringBuilder(s).reverse().toString()); // 使用StringBuilder类的reverse方法判断是否为回文串}
}
优化版
-
判断回文串的方法更高效:在这个版本中,使用了双指针的方法来判断子串是否为回文串。相比于前一个版本中使用
StringBuilder反转字符串再比较的方法,双指针的方法只需要遍历一次字符串,更加高效。 -
减少了不必要的字符串拷贝:在判断回文串时,这个版本直接使用了字符串的索引范围来进行判断,而不是通过
substring方法生成子串。这样可以避免创建新的字符串对象,减少了内存消耗和时间开销。
class Solution {List<List<String>> res = new ArrayList<>();public List<List<String>> partition(String s) {List<String> path = new ArrayList<>();backtrack(s, 0, path);return res;}public void backtrack(String s, int start, List<String> path) {if (start == s.length()) { // 结束条件res.add(new ArrayList<>(path));return;}for (int i = start; i < s.length(); i++) {if (isPalindrome(s, start, i)) { // 判断回文path.add(s.substring(start, i + 1)); // 做出选择backtrack(s, i + 1, path); // 递归进入下一层path.remove(path.size() - 1); // 撤销选择}}}public boolean isPalindrome(String s, int start, int end) {while (start < end) {if (s.charAt(start++) != s.charAt(end--)) {return false;}}return true;}
}