【算法】双指针-编程知识

快乐的流畅：个人主页

个人专栏：《算法神殿》《数据结构世界》《进击的C++》

远方有一堆篝火，在为久候之人燃烧！

文章目录

一、移动零
二、复写零
三、快乐数
四、盛最多水的容器
五、有效三角形的个数
六、和为s的两个数字
七、三数之和
八、四数之和
总结

一、移动零

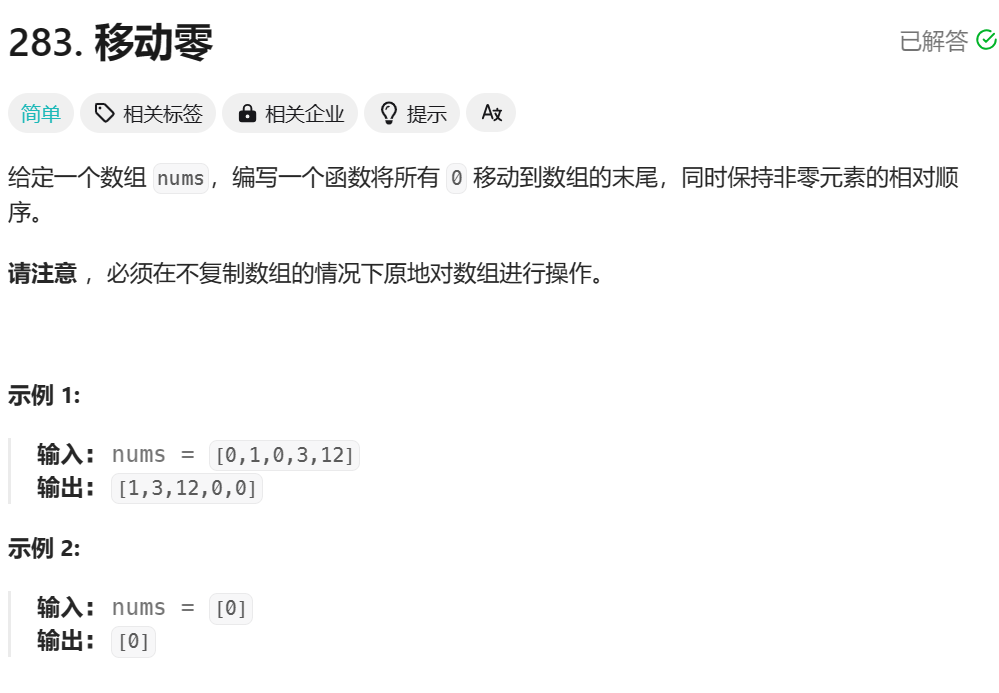
思路：

数组划分，快排核心步骤
cur从头到尾扫描，prev划分非零与零元素的区间

时间复杂度：O(N)

class Solution
{
public:void moveZeroes(vector<int>& nums){//双指针算法，数组划分//快排数据划分核心思想int prev = -1, cur = 0;while(cur < nums.size()){if(nums[cur] && ++prev != cur)//避免原地交换{swap(nums[prev], nums[cur]);}++cur;}}
};

二、复写零

思路：

从前往后模拟，找到最后一个要复写的元素
处理越界情况
从后往前复写

时间复杂度：O(N)

class Solution
{
public:void duplicateZeros(vector<int>& arr){//1.找到最后一个要复写的元素int dest = -1, cur = 0;while(1){if(arr[cur]){dest++;}else{dest += 2;}if(dest >= arr.size()-1){break;}cur++;}//2.处理越界情况if(dest == arr.size()){//此时arr[cur]一定为0arr[dest-1] = 0;dest -= 2;cur--;}//3.从后向前复写while(cur >= 0){if(arr[cur]){arr[dest] = arr[cur];dest--;}else{arr[dest-1] = arr[dest] = 0;dest -= 2;}cur--;}}
};

三、快乐数

思路：

迭代过程中必有循环（鸽巢原理）
快慢指针，判断相遇的值是否为1

时间复杂度：O(logN)

class Solution
{
public:int Happy(int n){int sum = 0;while(n){sum += (n%10)*(n%10);n /= 10;}return sum;}bool isHappy(int n){//快慢双指针int slow = n, fast = n;do{slow = Happy(slow);fast = Happy(Happy(fast));}while(slow != fast);return slow == 1;}
};

四、盛最多水的容器

思路：

利用单调性，舍去短板组合的讨论
左右双指针

时间复杂度：O(N)

class Solution
{
public:int maxArea(vector<int>& height){//利用单调性，左右双指针int maxV = 0;int left = 0, right = height.size()-1;while(left < right){int tmpV = 0;if(height[left] < height[right]){tmpV = height[left] * (right-left);++left;}else{tmpV = height[right] * (right-left);--right;}maxV = tmpV > maxV ? tmpV : maxV;}return maxV;}
};

五、有效三角形的个数

思路：

先排序优化
再每次固定最大的数
利用单调性，左右指针

时间复杂度：O(N²)

class Solution
{
public:int triangleNumber(vector<int>& nums){//先进行排序优化sort(nums.begin(), nums.end());//再固定最大的数int cur = nums.size()-1;int num = 0;while(cur >= 2){//利用单调性，左右指针int left = 0, right = cur-1;while(left < right){if(nums[left] + nums[right] > nums[cur]){num += right-left;--right;}else{++left;}}--cur;}return num;}
};

六、和为s的两个数字

思路：利用单调性，左右指针

时间复杂度：O(N)

class Solution
{
public:vector<int> FindNumbersWithSum(vector<int> nums,int sum){int left = 0, right = nums.size()-1, flag = 0;while(left < right){if(nums[left] + nums[right] < sum){++left;}else if(nums[left] + nums[right] > sum){--right;}else{flag = 1;break;}}vector<int> v;if(flag){v.push_back(nums[left]);v.push_back(nums[right]);}return v;}
};

七、三数之和

思路：

先排序优化
再固定一个数（小优化：固定的数<=0即可）
双指针算法
注意不重不漏（这里的细节和快排相似）：
- 不漏：找到后，不要停，缩小空间继续找
- 不重：遇到重复元素，不要停，继续缩小空间

时间复杂度：O(N²)

class Solution
{
public:vector<vector<int>> threeSum(vector<int>& nums){vector<vector<int>> vv;//先排序优化sort(nums.begin(), nums.end());//再固定一个数，利用双指针算法int cur = 0, n = nums.size();while(cur < n && nums[cur] <= 0)//固定的优化{int sum = -nums[cur];int left = cur+1, right = n-1;while(left < right){if(nums[left] + nums[right] < sum){++left;}else if(nums[left] + nums[right] > sum){--right;}else{vv.push_back({nums[cur], nums[left], nums[right]});//不漏：不要停，缩小区间继续找//不重：相同元素不要停，继续缩小区间int tmpL = nums[left], tmpR = nums[right];while(left < right && nums[left] == tmpL)//防止越界{++left;}while(left < right && nums[right] == tmpR)//防止越界{--right;}}}int tmpC = nums[cur];while(cur < n && nums[cur] == tmpC)//防止越界{++cur;}}return vv;}
};

八、四数之和

思路：与三数之和类似，多加上一个固定的数

时间复杂度：O(N³)

class Solution
{
public:vector<vector<int>> fourSum(vector<int>& nums, int target){vector<vector<int>> vv;//排序优化sort(nums.begin(), nums.end());//固定两个数，进行双指针算法int prev = 0, n = nums.size();while(prev < n){int cur = prev+1;while(cur < n){int left = cur+1, right = n-1;long long newTarget = (long long)target-nums[cur]-nums[prev];//防止数据溢出while(left < right){int sum = nums[left]+nums[right];if(sum < newTarget){++left;}else if(sum > newTarget){--right;}else{vv.push_back({nums[prev], nums[cur], nums[left], nums[right]});int tmpL = nums[left], tmpR = nums[right];while(left < right && nums[left] == tmpL){++left;}while(left < right && nums[right] == tmpR){--right;}}}int tmpC = nums[cur];while(cur < n && nums[cur] == tmpC){++cur;}}int tmpP = nums[prev];while(prev < n && nums[prev] == tmpP){++prev;}}return vv;}
};