《剑指 Offer》专项突破版 - 面试题 95、96 和 97 : 和动态规划相关的双序列问题（C++ 实现）-编程知识

前言

面试题 95 : 最长公共子序列

面试题 96 : 字符串交织

面试题 97 : 子序列的数目

前言

和单序列问题不同，双序列问题的输入有两个或更多的序列，通常是两个字符串或数组。由于输入是两个序列，因此状态转移方程通常有两个参数，即 f(i, j)，定义第 1 个序列中下标从 0 到 i 的子序列和第 2 个序列中下标从 0 到 j 的子序列的最优解（或解的个数）。一旦找到了 f(i, j) 与 f(i - 1, j - 1)、f(i - 1, j) 和 f(i, j - 1) 的关系，通常问题也就迎刃而解。

由于双序列的状态转移方程有两个参数，因此通常需要使用一个二维数组来保存状态转移方程的计算结果。但在大多数情况下，可以优化代码的空间效率，只需要保存二维数组的一行就可以完成状态转移方程的计算，因此可以只用一个一维数组就能实现二维数组的缓存功能。

接下来通过几个典型的编程题目来介绍如何应用动态规划解决双序列问题。

面试题 95 : 最长公共子序列

题目：

输入两个字符串，请求出它们的最长公共子序列的长度。如果从字符串 s1 中删除若干字符之后能得到 s2，那么字符串 s2 就是字符串 s1 的一个子序列。例如，从字符串 "abcde" 中删除两个字符之后能得到字符串 "ace"，因此字符串 "ace" 是字符串 "abcde" 的一个子序列。但字符串 "aec" 不是字符串 "abcde" 的子序列。如果输入字符串 "abcde" 和 "badfe"，那么它们的最长公共子序列是 "bde"，因此输出 3。

分析：

两个字符串可能存在多个公共子序列，如果空字符串 ""、"a"、"ad" 与 "bde" 等都是字符串 "abcde" 和 "badfe" 的公共子序列。这个题目没有要求列出两个字符串的所有公共子序列，而只是计算最长公共子序列的长度，也就是求问题的最优解，因此可以考虑应用动态规划来解决这个问题。

分析确定状态转移方程：

应用动态规划解决问题的关键在于确定状态转移方程。由于输入有两个字符串，因此状态转移方程有两个参数。用函数 f(i, j) 表示第 1 个字符串中下标从 0 到 i 的子字符串（记为 s1[0···i]）和第 2 个字符串中下标从 0 到 j 的子字符串（记为 s2[0···j]）的最长公共子序列的长度。如果第 1 个字符串的长度是 m，第 2 个字符串的长度是 n，那么 f(m - 1, n - 1) 就是整个问题的解。

如果第 1 个字符串中下标为 i 的字符（记为 s1[i]）与第 2 个字符串中下标为 j 的字符（记为 s2[j]）相同，那么 f(i, j) 相当于在 s1[0···i-1] 和 s2[0···j-1] 的最长公共子序列的后面添加一个公共字符，也就是 f(i, j) = f(i - 1, j - 1) + 1。

如果字符 s1[i] 与字符 s2[j] 不相同，则这两个字符不可能同时出现在 s1[0···i] 和 s2[0···j] 的公共子序列中。此时 s1[0···i] 和 s2[0···j] 的最长公共子序列要么是 s1[0···i-1] 和 s2[0···j] 的最长公共子序列，要么是 s1[0···i] 和 s2[0···j-1] 的最长公共子序列。也就是说，此时 f(i, j) 是 f(i - 1, j) 和 f(i, j - 1) 的最大值。

可以将这个问题的转移转移方程总结为：

当上述状态转移方程的 i 或 j 等于 0 时，即求 f(0, j) 或 f(i, 0) 时可能需要 f(-1, j) 或 f(i, -1) 的值。f(0, j) 的含义是 s1[0···0] 和 s2[0···j] 这两个子字符串的最长公共子序列的长度，即第 1 个子字符串只包含一个下标为 0 的字符，那么 f(-1, j) 对应的第 1 个字符串再减少一个字符，所以第 1 个子字符串是空字符串。任意空字符串和另一个字符串的公共子序列的长度都是 0，所以 f(-1, j) 的值等于 0。同理，f(i, -1) 的值也等于 0。

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size(), n = text2.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for (int i = 0; i < m; ++i){for (int j = 0; j < n; ++j){if (text1[i] == text2[j])dp[i + 1][j + 1] = dp[i][j] + 1;elsedp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);}}return dp[m][n];}
};

由于表格中有 i 等于 -1 对应的行和 j 等于 -1 对应的列，因此如果输入字符串的长度分别为 m、n，那么代码中的二维数组 dp 的行数和列数分别是 m + 1 和 n + 1。f(i, j) 的值保存在 dp[i + 1][j + 1] 中。

这种解法的空间复杂度和时间复杂度都是 O(mn)。

优化空间效率，只保存表格中的两行：

需要注意的是，f(i, j) 的值依赖于表格中左上角 f(i - 1, j - 1) 的值、正上方 f(i - 1, j) 的值和同一行左边 f(i, j - 1) 的值。由于计算 f(i, j) 的值时只需要使用上方一行的值和同一行左边的值，因此实际上只需要保存表格中的两行就可以。

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size(), n = text2.size();if (m < n)return longestCommonSubsequence(text2, text1);
vector<vector<int>> dp(2, vector<int>(n + 1, 0));for (int i = 0; i < m; ++i){for (int j = 0; j < n; ++j){if (text1[i] == text2[j])dp[(i + 1) % 2][j + 1] = dp[i % 2][j] + 1;elsedp[(i + 1) % 2][j + 1] = max(dp[i % 2][j + 1], dp[(i + 1) % 2][j]);}}return dp[m % 2][n];}
};

在上述代码中，二维数组 dp 只有两行，f(i, j) 的值保存在 dp[(i + 1) % 2][j + 1] 中。由于数组 dp 的行数是一个常数，因此此时的空间复杂度是 O(min(m, n))。由于仍然需要二重循环，因此时间复杂度仍然是 O(mn)。

进一步优化空间效率，只需要一个一维数组：

还可以进一步优化空间效率，只需要用一个一维数组就能保存所有计算所需的信息。这个一维数组的长度是表格的列数（即输入字符串 s2 的长度加 1）。为了让一个一维数组保存表格中的两行信息，一维数组的每个位置需要保存原来表格中上下两格的信息，即 f(i, j) 和 f(i - 1, j) 都保存在数组 dp 下标 j + 1 的位置。在计算 f(i, j) 之前，dp[j + 1] 中保存的是 f(i - 1, j) 的值；在完成 f(i, j) 的计算之后，dp[j + 1] 被 f(i, j) 的值替换。

需要注意的是，在计算 f(i, j + 1) 时，可能还需要 f(i - 1, j) 的值，因此在计算 f(i, j) 之后不能直接用 f(i, j) 的值替换 dp[j + 1] 中 f(i - 1, j) 的值。可以在用 f(i, j) 的值替换 dp[j + 1] 中 f(i - 1, j) 的值之前先将 f(i - 1, j) 的值临时保存起来，这样下一步在计算 f(i, j + 1) 时还能得到 f(i - 1, j) 的值。

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m = text1.size(), n = text2.size();if (m < n)return longestCommonSubsequence(text2, text1);vector<int> dp(n + 1, 0);for (int i = 0; i < m; ++i){int prev = dp[0];for (int j = 0; j < n; ++j){int cur;if (text1[i] == text2[j])cur = prev + 1;elsecur = max(dp[j + 1], dp[j]);
prev = dp[j + 1];dp[j + 1] = cur;}}return dp[n];}
};

虽然再次优化之后的空间复杂度仍然是 O(min(m, n))，但所需的辅助空间减少到之前的一半。

面试题 96 : 字符串交织

题目：

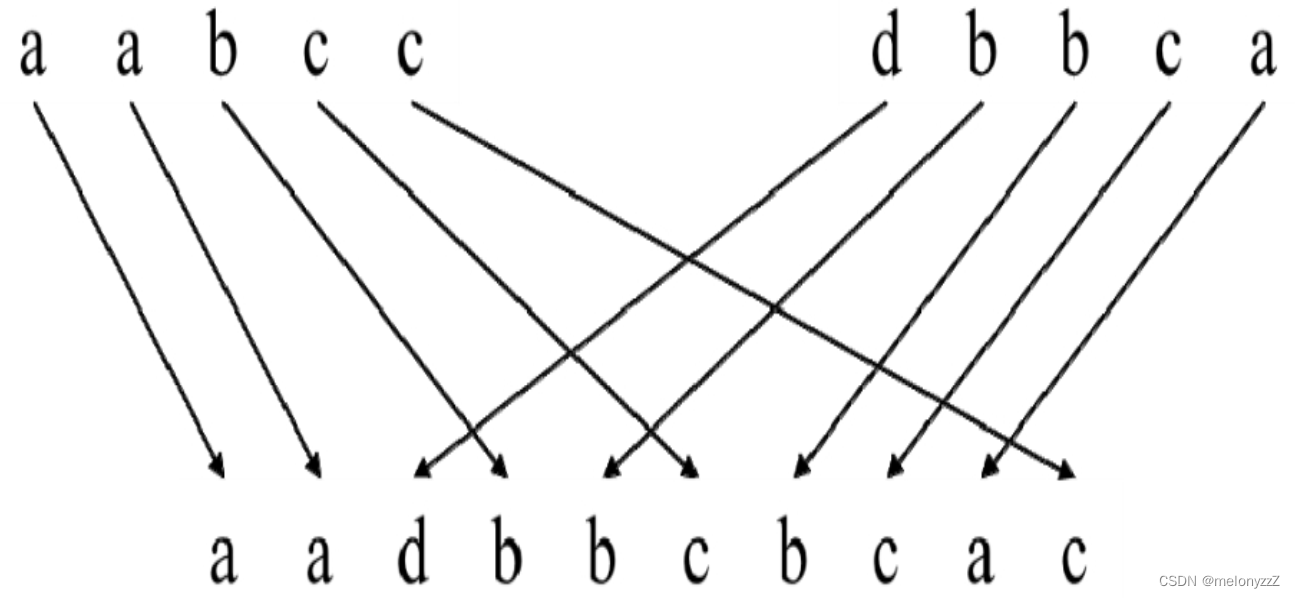
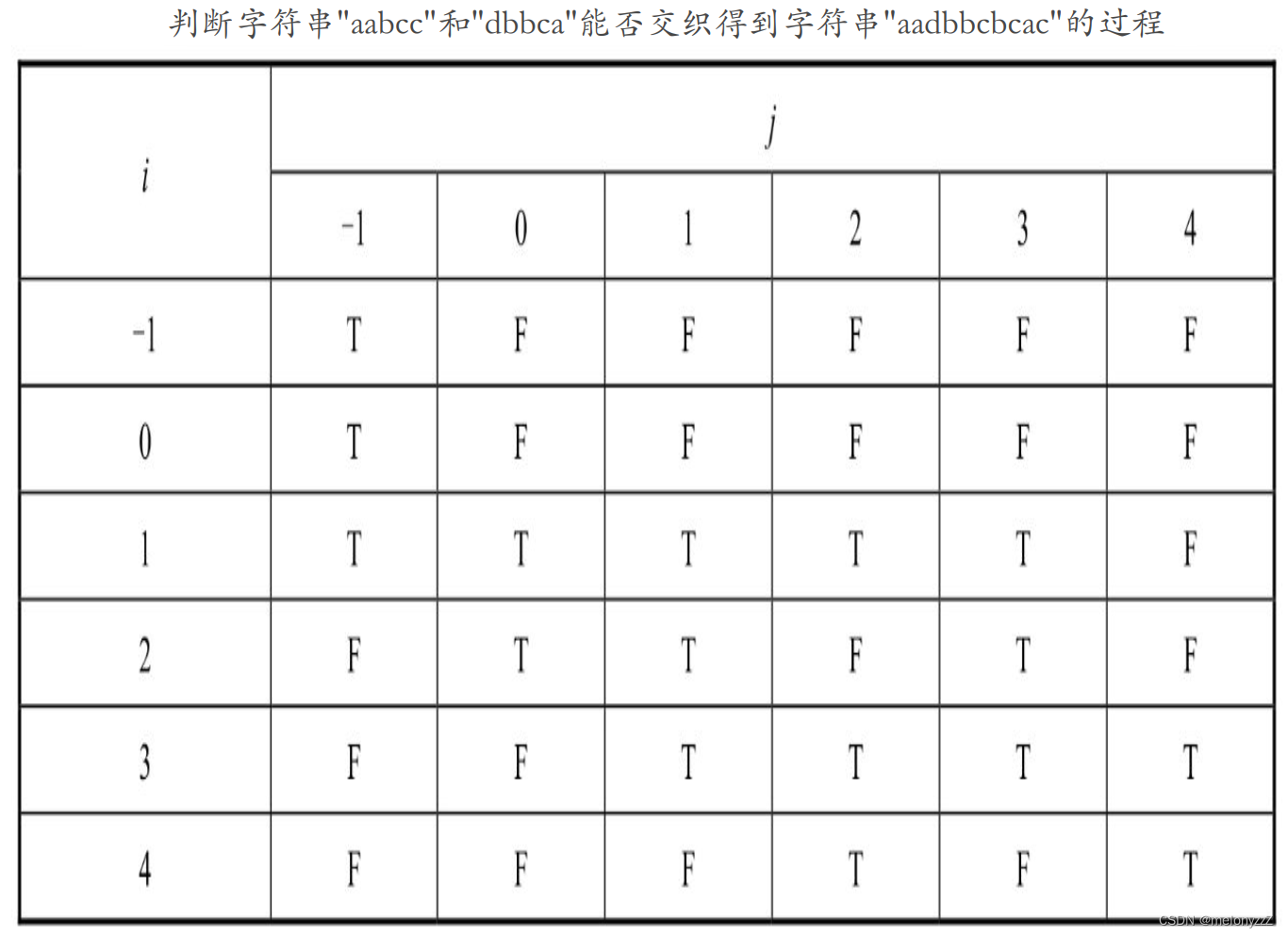
输入 3 个字符串 s1、s2 和 s3，请判断字符串 s3 能不能由字符串 s1 和 s2 交织而成，即字符串 s3 的所有字符都是字符串 s1 或 s2 中的字符，字符串 s1 和 s2 中的字符都将出现在字符串 s3 中且相对位置不变。例如，字符串 "aadbbcbcac" 可以由字符串 "aabcc" 和 "dbbca" 交织而成，如下图所示。

分析：

每步从字符串 s1 或 s2 中选出一个字符交织生成字符串 s3 中的一个字符，那么交织生成字符串 s3 中的所有字符需要多个步骤。每个步骤既可能从字符串 s1 中选择一个字符，也可能从字符串 s2 中选择一个字符，也就是说，每步可能面临两个选择。完成一件事情需要多个步骤，而且每步都可能面临多个选择，这个问题看起来可以用回溯法解决。

这个问题并没有要求列出所有将字符串 s1 和 s2 交织得到字符串 s3 的方法，而只是判断能否将字符串 s1 和 s2 交织得到字符串 s3。如果能够将字符串 s1 和 s2 交织得到字符串 s3，那么将字符串 s1 和 s2 交织得到字符串 s3 的方法的数目大于 0。这只是判断问题的解是否存在（即判断解的数目是否大于 0），因此这个问题更适合应用动态规划来解决。

分析确定状态转移方程：

应用动态规划解决问题的关键在于找出问题的状态转移方程。如果字符串 s1 的长度为 m，字符串 s2 的长度为 n，那么它们交织得到的字符串 s3 的长度一定是 m + n。可以用函数 f(i, j) 表示字符串 s1 的下标从 0 到 i 的子字符串（记为 s1[0···i]，长度为 i + 1）和字符串 s2 的下标从 0 到 j 的子字符串（记为 s2[0···j]，长度为 j + 1）能否交织得到字符串 s3 的下标从 0 到 i + j + 1 的子字符串（记为 s3[0···i+j+1]，长度为 i + j + 2）。f(m - 1, n - 1) 就是整个问题的解。

按照字符串的交织规则，字符串 s3 的下标为 i + j + 1 的字符（s3[i + j + 1]）既可能是来自字符串 s1 的下标为 i 的字符（s1[i]），也可能是来自字符串 s2 的下标为 j 的字符（s2[j]）。如果 s3[i + j + 1] 和 s1[i] 相同，只要 s1[0···i-1] 和 s2[0···j] 能交织得到子字符串 s3[0···i+j]，那么 s1[0···i] 一定能和 s2[0···j] 交织得到 s3[0···i+j+1]。也就是说，当 s3[i + j + 1] 和 s1[i] 相同时，f(i, j) 的值等于 f(i - 1, j) 的值。类似地，当 s3[i + j + 1] 和 s2[j] 相同时，f(i, j) 的值等于 f(i, j - 1) 的值。如果 s1[i] 和 s2[j] 都和 s3[i + j + 1] 相同，此时只要 f(i - 1, j) 和 f(i, j - 1) 有一个值为 true，那么 f(i, j) 的值为 true。

可以将这个问题的状态转移方程总结为：

由此可知，f(i, j) 的值依赖于 f(i - 1, j) 和 f(i, j - 1) 的值。如果 i 等于 0，那么 f(0, j) 的值依赖于 f(-1, j) 和 f(0, j - 1) 的值。状态转移方程中的 i 是指字符串 s1 中当前处理的子字符串的最后一个字符的下标。当 i 等于 0 时，当前处理的字符串 s1 的子字符串中只有一个下标为 0 的字符。那么当 i 等于 -1 时，当前处理的字符串 s1 的子字符串中一个字符也没有，是空的。f(-1, j) 的含义是当字符串 s1 的子字符串是空字符串的时候，它和字符串 s2 中下标从 0 到 j 的子字符串（即 s2[0···j]）能否交织出字符串 s3 中下标从 0 到 j 的子字符串（即 s3[0···j]）。由于空字符串和 s2[0···j] 交织的结果一定还是 s2[0···j]，因此 f(-1, j) 的值其实取决于子字符串 s2[0···j] 和 s3[0···j] 是否相同。如果 s2[j] 和 s3[j] 不同，那么 f(-1, j) 的值为 false；如果 s2[j] 和 s3[j] 相同，那么 f(-1, j) 的值等于 f(-1. j - 1) 的值。

类似地，f(i, -1) 的含义是当字符串 s2 的子字符串是空字符串时，它和 s1[0···i] 能否交织得到 s3[0···i]，因此 f(i, -1) 的值取决于子字符串 s1[0···i] 和 s3[0···i] 是否相同。如果 s1[i] 和 s3[i] 不同，那么 f(i, -1) 的值为 false；如果 s1[i] 和 s3[i] 相同，那么 f(i, -1) 的值等于 f(i - 1, -1) 的值。

当 i 和 j 都等于 -1 时，f(-1, -1) 的值的含义是两个空字符串能否交织得到一个空字符串。这显然是可以的，因此 f(-1, -1) 的值为 true。

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size(), n = s2.size();if (m + n != s3.size())return false;
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));dp[0][0] = true;for (int j = 0; j < n; ++j){dp[0][j + 1] = s2[j] == s3[j] && dp[0][j];}for (int i = 0; i < m; ++i){dp[i + 1][0] = s1[i] == s3[i] && dp[i][0];}
for (int i = 0; i < m; ++i){for (int j = 0; j < n; ++j){dp[i + 1][j + 1] = (s1[i] == s3[i + j + 1] && dp[i][j + 1])|| (s2[j] == s3[i + j + 1] && dp[i + 1][j]);}}return dp[m][n];}
};

在上述代码中，输入的两个字符串的长度分别是 m 和 n，二维数组 dp 的行数和列数分别是 m + 1 和 n + 1，f(i, j) 的值保存在 dp[i + 1][j + 1] 的位置。先确定 f(-1, j) 和 f(i, -1) 的值，再用一个二重循环根据状态转移方程计算其余的 f(i, j) 的值。

上述代码的时间复杂度和空间复杂度都是 O(mn)。

优化空间效率：

由于 f(i, j) 的值只依赖于 f(i - 1, j) 和 f(i, j - 1) 的值，因此计算数组 dp 的行号为 i + 1 的位置时只需要用上面行号为 i 的一行的值，即只需要保留二维数组中的两行就可以。当数组 dp 只有两行时，f(i, j) 的值保存在 dp[(i + 1) % 2][j + 1] 中。

还可以进一步优化空间效率，只需要保存二维数组中的一行就可以。f(i, j) 的值依赖于位于它上方的 f(i - 1, j) 和它左方的 f(i, j - 1)，因此在计算 f(i, j + 1) 时只依赖 f(i - 1, j + 1) 和 f(i, j) 的值。f(i - 1, j) 的值在计算出 f(i, j) 之后就不再需要，因此可以用同一个位置保存 f(i - 1, j) 和 f(i, j) 的值。该位置在 f(i, j) 计算之前保存的是 f(i - 1, j) 的值，一旦计算出 f(i, j) 的值之后就替换 f(i - 1, j)。这时会丢失 f(i - 1, j) 的值，但不会导致任何问题，因为以后的计算不再需要 f(i - 1, j) 的值。

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size(), n = s2.size();if (m + n != s3.size())return false;if (m < n)return isInterleave(s2, s1, s3);vector<bool> dp(n + 1);dp[0] = true;for (int j = 0; j < n; ++j){dp[j + 1] = s2[j] == s3[j] && dp[j];}
for (int i = 0; i < m; ++i){dp[0] = s1[i] == s3[i] && dp[0];for (int j = 0; j < n; ++j){dp[j + 1] = (s1[i] == s3[i + j + 1] && dp[j + 1]) || (s2[j] == s3[i + j + 1] && dp[j]);}}return dp[n];}
};

优化之后的代码的时间复杂度仍然是 O(mn)，但空间效率变成 O(min(m, n))。

面试题 97 : 子序列的数目

题目：

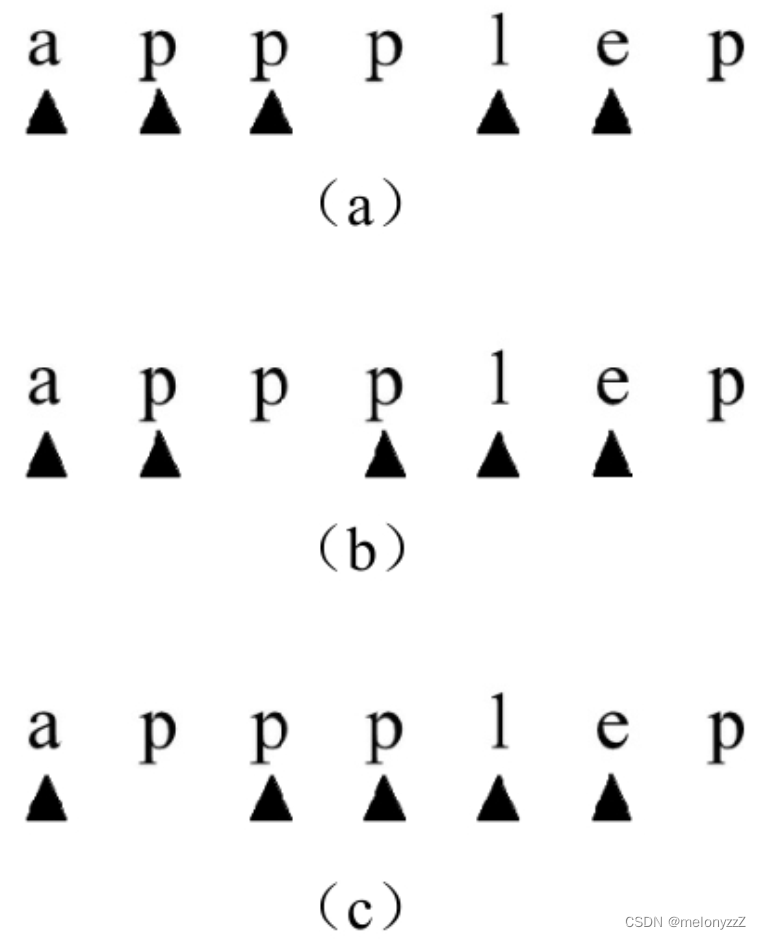
输入字符串 S 和 T，请计算字符串 S 中有多少个子序列等于字符串 T。例如，在字符串 "appplep" 中，有 3 个子序列等于字符串 "apple"，如下图所示。

分析：

为了解决这个问题，每步从字符串 S 中取出一个字符判断它是否和字符串 T 中的某个字符匹配。字符串 S 中的字符可能和字符串 T 中的多个字符匹配，如字符串 T 中的字符 'p' 可能和字符串 S 中的 3 个 'p' 匹配，因此每一步可能面临多个选择。解决一个问题需要多个步骤，并且每步都可能面临多个选择，这看起来很适合运用回溯法。但由于这个问题没有要求列出字符串 S 中所有等于字符串 T 的子序列，而是只计算字符串 S 中等于字符串 T 的子序列的数目，也就是求解数目，因此，这个问题更适合运用动态规划来解决。

分析确定状态转移方程：

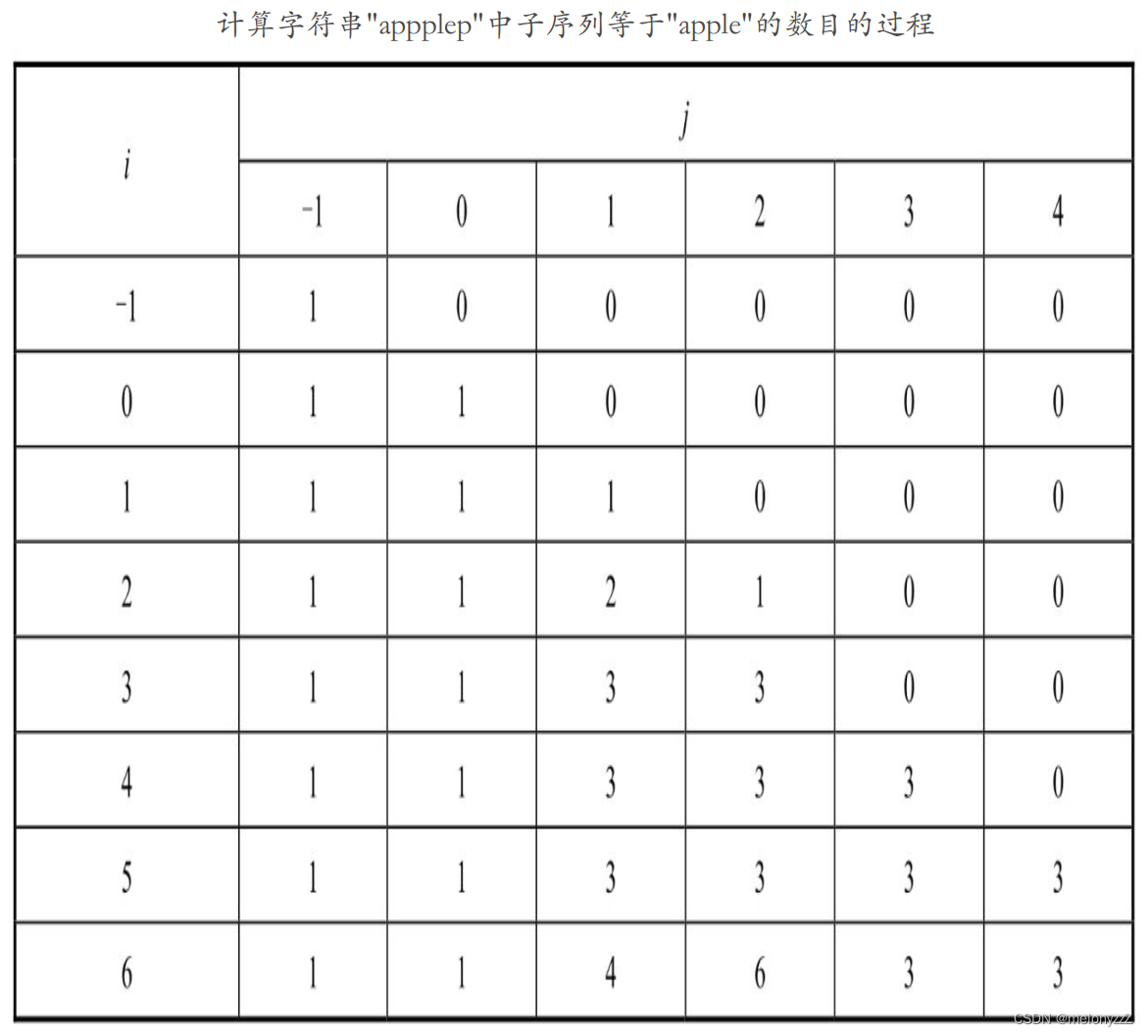
应用动态规划解决问题的关键在于找出状态转移方程。由于这个问题的输入有两个字符串，因此状态转移方程有两个参数。用 f(i, j) 表示字符串 S 下标从 0 到 i 的子字符串（记为 S[0···i]）中等于字符串 T 下标从 0 到 j 的子字符串（记为 T[0···j]）的子序列的数目。如果字符串 S 的长度是 m，字符串 T 的长度是 n，那么 f(m - 1, n - 1) 就是字符串 S 中等于字符串 T 的子序列的数目。

当 S[0···i] 的长度小于 T[0···j] 的长度时，S[0···i] 中不可能存在等于 T[0···j] 的子序列，所以当 i 小于 j 时，f(i, j) 的值都等于 0。

如果字符串 S 中下标为 i 的字符（记为 S[i]）等于字符串 T 中下标为 j 的字符（记为 T[j]），那么对 S[i] 有两个选择：一个是用 S[i] 去匹配 T[j]，那么 S[0···i] 中等于 T[0···j] 的子序列的数目等于 S[0···i-1] 中等于 T[0···j-1] 的子序列的数目；另一个是舍去 S[i]，那么 S[0···i] 中等于 T[0···j] 的子序列的数目等于 S[0···i-1] 中等于 T[0···j] 的子序列的数目。因此，当 S[i] 等于 T[j] 时，f(i, j) 等于 f(i - 1, j - 1) + f(i - 1, j)。

如果 S[i] 和 T[j] 不相同，则只能舍去 S[i]，此时 f(i, j) 等于 f(i - 1, j)。

f(-1, -1) 等于 1；f(-1, j) 等于 0（j >= 0）；f(i, -1) 等于 1（i >= 0）。

class Solution {
public:int numDistinct(string s, string t) {int m = s.size(), n = t.size();vector<vector<unsigned long>> dp(m + 1, vector<unsigned long>(n + 1, 0));dp[0][0] = 1;
for (int i = 0; i < m; ++i){dp[i + 1][0] = 1;for (int j = 0; j <= i && j < n; ++j){if (s[i] == t[j])dp[i + 1][j + 1] = dp[i][j] + dp[i][j + 1];elsedp[i + 1][j + 1] = dp[i][j + 1];}}return dp[m][n];}
};

上述代码中二维数组的行数为 m + 1，列数为 n + 1，f(i, j) 的值保存在 dp[i + 1][j + 1] 中。

代码的时间复杂度和空间复杂度都是 O(mn)。

优化空间效率：

在计算 f(i, j) 的值时，最多只需要用到它上一行 f(i - 1, j - 1) 和 f(i - 1, j) 的值，因此可以只保存表格中的两行。可以创建一个只有两行的二维数组 dp，列数仍然是 n + 1，将 f(i, j) 保存在 dp[(i + 1) % 2][j + 1] 中。

还可以进一步优化空间效率。如果能够将 f(i, j) 和 f(i - 1, j) 保存到数组中的同一个位置，那么实际上只需一个长度为 n + 1 的一维数组。

如果按照从上到下、从左到右的顺序计算并填充表格，则先计算 f(i, j)，再计算 f(i, j + 1)。计算 f(i, j + 1) 时可能需要用到 f(i - 1, j) 和 f(i - 1, j + 1) 的值。假设将 f(i, j) 和 f(i - 1, j) 都保存在 dp[j + 1] 中，那么在 f(i, j) 计算完成之后将会覆盖原先保存在 dp[j + 1] 中的 f(i - 1, j)，这会影响下一步计算 f(i, j + 1)。可以在用 f(i, j) 覆盖原先保存在 dp[j + 1] 中的 f(i - 1, j) 之前先将 f(i - 1, j) 保存下来，用于接下来计算 f(i, j + 1)。
由于计算 f(i, j) 只依赖位于它上一行的 f(i - 1, j - 1) 和 f(i - 1, j)，并不依赖于 f(i, j - 1)，因此不一定要按照从左到右的顺序计算 f(i, j)。如果按照从右到左的顺序，则先计算 f(i, j) 再计算 f(i, j - 1)。计算 f(i, j - 1) 可能会用到 f(i - 1, j - 2) 和 f(i - 1, j - 1)。如果计算完 f(i, j) 之后将它保存到 dp[j + 1] 中并覆盖 f(i - 1, j)，则不会影响下一步计算 f(i, j - 1)。

按照从上到下、从右到左的顺序计算 f(i, j) 的参考代码如下：

class Solution {
public:int numDistinct(string s, string t) {int m = s.size(), n = t.size();vector<unsigned long> dp(n + 1, 0);dp[0] = 1;
for (int i = 0; i < m; ++i){for (int j = min(i, n - 1); j >= 0; --j){if (s[i] == t[j])dp[j + 1] += dp[j];}}return dp[n];}
};