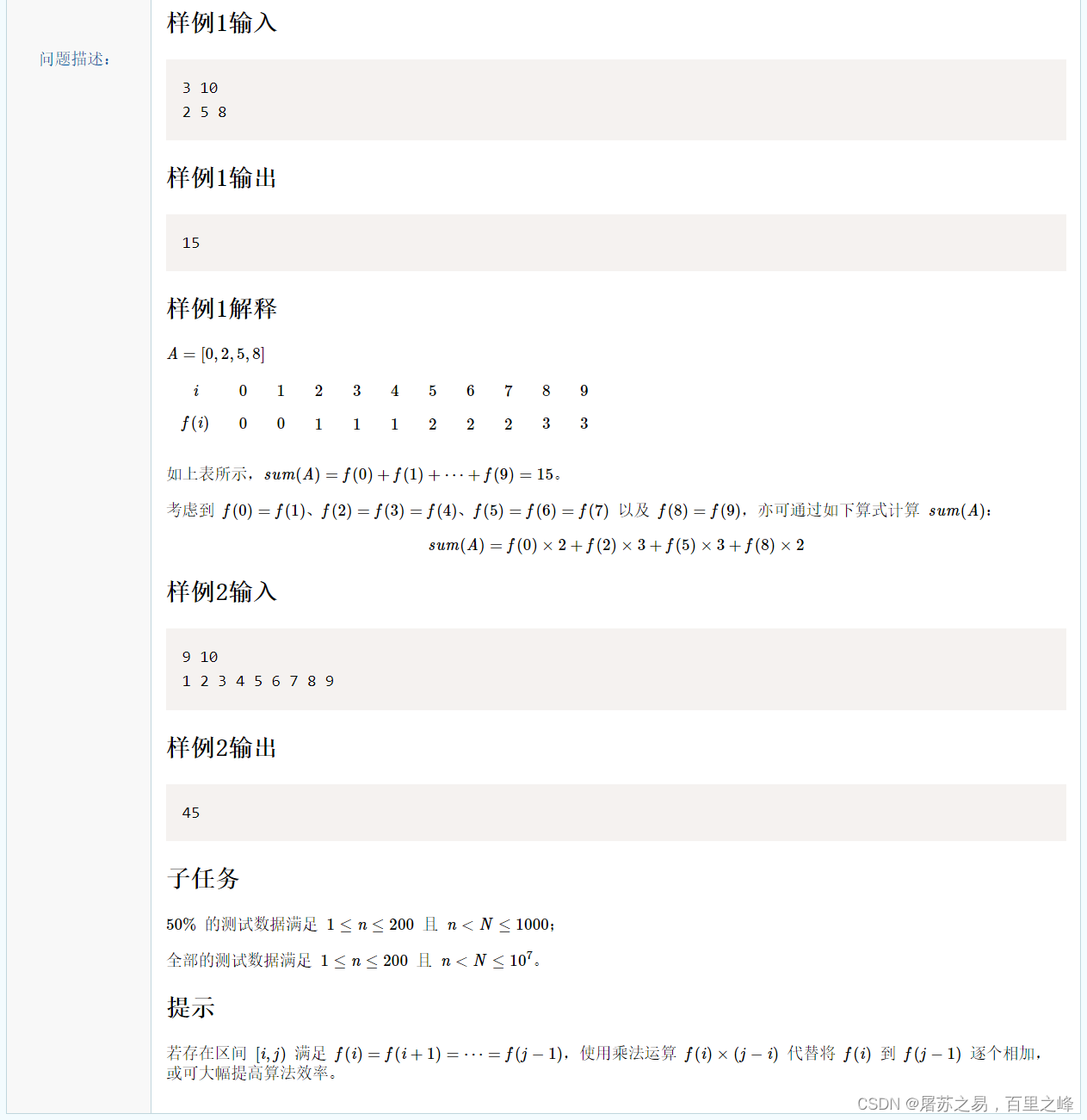
回溯理论

• 回溯法就是递归函数，纯暴力搜索

解决的问题

1. 组合（无顺序） 1 2 3 4 给出大小为2的所有组合

2. 切割字符串

3. 子集问题 1 2 3 4，子集有1 2 3 4,12,13,14，…123 124…

4. 排列（有顺序）

5. 棋盘问题 N皇后

理解回溯

• 抽象成一个n叉树，树的宽度就是集合的大小

• 关键：恢复现场

• 回溯法模板：

void backtracking(参数) {if(终止条件) {收集结果;return;}for(遍历集合里的每个元素) {处理节点;递归函数;恢复现场;}return;
}

77.组合

• 本题如果纯for循环暴力的话，k个元素就要嵌套k个for循环。

回溯法的话，就是递归k层。

树形结构

怎么控制每次从哪里开始取？通过每次递归传入一个startIndex控制开始取的下标

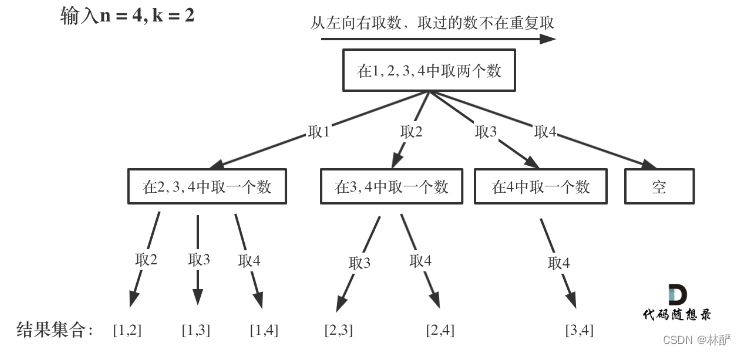
回溯三部曲

1. 回溯函数的参数

用一个List path存储所有的可能，收集满后放到二维list里。这俩定义成全局变量。

• 需要哪些参数？范围n，个数k，以及开始的范围startIndex=1

void backtracking(int n, int k,int startIndex)

• 终止条件 到叶子节点了，path大小=k，收获结果

if(path.size() == k) {result.add(path);  //收集结果return;
}

• 单层递归逻辑

  for循环，用path收集路径上的元素，然后递归下一层（起始位置i+1）+恢复现场

for(i = startIndex, i <= n; i++) {path.add(i);backtracking(n,k,i+1);path.removeLast();   //恢复现场
}

剪枝

剪枝剪的是孩子，在for循环里完成的，修改i开始遍历的位置，如果元素个数不够了就提前剪掉。

什么时候停止搜索呢？

• path.size()是已经选取的元素的大小
• 还剩k-path.size()个元素要选
• 至多从n-(k-path.size()) + 1的位置开始搜索！再往后一个就满足不了要求了

n-i>=k-path.size(列表剩余元素数目>=所需元素数目)，加不加1依照实际情况决定。

举个例子：假设n=4,k=3，path里0个元素。至多从4-(3-0)+1=2，至多从2开始

for(int i = startIndex; i <= n-(k-path.size())+1; i++)

• 完整java代码

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new LinkedList<>();public void backtracking(int n, int k, int startIndex) {if(path.size() == k) {result.add(new ArrayList<>(path));return;}for(int i = startIndex; i <= n - (k-path.size())+1; i++) {path.add(i);backtracking(n,k,i+1);path.removeLast();}}public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return result;}
}

注意：result用ArrayList，path用List接口的LinkedList，恢复现场用removeLast。收集结果时要new ArrayList<>(path)