题目描述:
输入一个长度为 n 的整数序列,从中找出一段长度不超过 m 的连续子序列,使得子序列中所有数的和最大。
注意: 子序列的长度至少是 1。
输入格式:
第一行输入两个整数 n,m。
第二行输入 n 个数,代表长度为 n 的整数序列。
同一行数之间用空格隔开
输出格式:
输出一个整数,代表该序列的最大子序和。
数据范围:
1≤n,m≤300000
保证所有输入和最终结果都在 int 范围内。
输入样例:
6 4
1 -3 5 1 -2 3
输出样例:
7分析步骤:
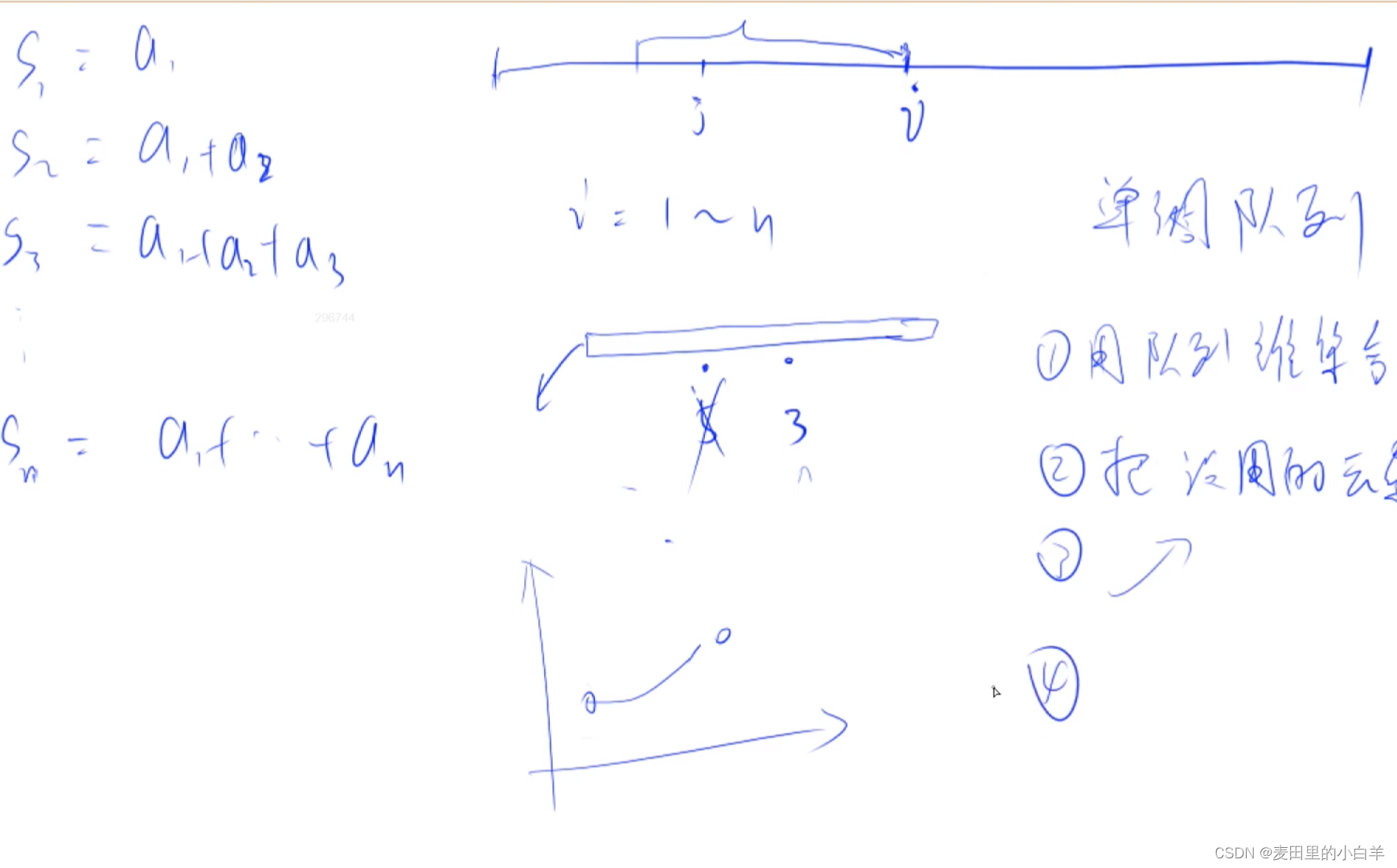
第一:我们观查题目后,我们可以得知,我们是需要求出一段区间之内的最大的和,这就非常简单的联想到了和区间和有关系,区间和又与前缀和有关,那么至此我们第一个特点就分析出来了,本题目要运用前缀和。
第二:其次,我们需要找的是一个最值,我们可以运用一个队列来维护我们的区间和的值,并且将没有用的之直接剔除出去,例如:我们寻找最小值,如果刚要进入队列的值比队列之中的任何一个都要小,那么我们只要这个队列的里的值都清理出去,就可以保持对头一定是最小的那个值,后面来了比这个值大的数直接放入队列之中就可以,因为这个数没有对头的数小。那么这样就可以将队列维护成一个单调的队列,只需要在O(1)的时间度内就可以找到最值,那么我们就应该想到用单调队列,解决此问题。
-
所以用单调队列的思考顺序是这样的:
-
用队列维护集合;
-
把没有用的值给他剔除出去;
-
该队列会呈现单调的特点;
-
在O(1)时间找最值
第三:书写主函数,构建整体框架:
-
由于之前,我们分析出了要用前缀和所以我们将前缀和算出来
cin>>n>>m;for(int i = 1 ; i <= n ; i ++){cin>>arr[i];arr[i] += arr[i-1];} -
其次定义我们的队头节点,和队尾节点为0。定义res为负无穷,为了更好的更新答案。
-
用for循环去遍历我们之前算出来的前缀和数组。
-
进入for循环判断是否出了队头,因为 i 是不断的向前面去遍历只要对头位置 小于 i减去m(窗口的大小)那么就证明队伍的长度大小太大了,那么队伍头部就应该弹出;
-
在动态更新一下我们的答案;
-
进入我们的while循环,只要队列之中还有数,并且队伍尾部的值大于等于刚刚要进来队列的值的话我们的尾部节点就一直向后退去,直到我们这个队伍之中比刚刚进来的这个数的值要大的都退出队伍了的话,我们的目的就达到了,现在队列就是一个单调队列。
-
因为上一步尾部节点只是向后退,现在就将其入队就可以了。
for(int i = 1 ; i <= n ; i ++){if(q[hh] < i - m )hh++;res = max(res , arr[i] - arr[q[hh]]);while(hh <= tt and arr[q[tt]] >= arr[i]) tt--;q[++tt] = i;}现在我们总结一下单调队列的模板应该怎么写:
-
首先判断队伍的长度是否符合题目的要求,也就是单调队列的大小与题目要求的大小一不一至,如果超过了题目的要求就让队头出队。
-
动态更新我们的值
-
确定我们这个单调队列是求最大值还是最小值,如果是求单调递增的队列那么队伍尾部就得比刚刚进来的数要大于或等于;如果是求单调递减的队列那么队伍尾部就得小于等于刚刚进来的数
-
入队刚刚要进队列的数。
这就是单调队列的模板,各位可以记一记如果在蓝桥杯的考试之中遇到了单调队列,可以得心应手。单调队列其实就是我们之前学过的滑动窗口大家也可以看看这个题解,这个题目更基础更加容易懂。其次二维的单调队列也是比较独特的大家可以看看这道题解子矩阵。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;
typedef long long LL;const int N = 3e5+10;LL n,m;
LL arr[N];
LL q[N];int main()
{cin>>n>>m;for(int i = 1 ; i <= n ; i ++){cin>>arr[i];arr[i] += arr[i-1];}int tt = 0 , hh = 0 ; LL res = -0x3f3f3f3f3f3f3f;for(int i = 1 ; i <= n ; i ++){if(q[hh] < i - m )hh++;res = max(res , arr[i] - arr[q[hh]]);while(hh <= tt and arr[q[tt]] >= arr[i]) tt--;q[++tt] = i;}cout<<res;return 0;
}