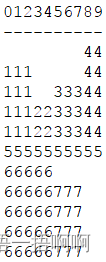题目描述
小明需要在一篇文档中加入 N 张图片,其中第 i 张图片的宽度是 Wi,高度是 Hi。
假设纸张的宽度是 M,小明使用的文档编辑工具会用以下方式对图片进行自动排版:1. 该工具会按照图片顺序,在宽度 M 以内,将尽可能多的图片排在一行。该行的高度是行内最高的图片的高度。例如在 M=10 的纸张上依次打印 3x4, 2x2, 3x3 三张图片,则效果如下图所示,这一行高度为4。(分割线以上为列标尺,分割线以下为排版区域;数字组成的矩形为第x张图片占用的版面)
2. 如果当前行剩余宽度大于0,并且小于下一张图片,则下一张图片会按比例缩放到宽度为当前行剩余宽度(高度向上取整),然后放入当前行。例如再放入一张4x9的图片,由于剩余宽度是2,这张图片会被压缩到2x5,再被放入第一行的末尾。此时该行高度为5:
3. 如果当前行剩余宽度为0,该工具会从下一行开始继续对剩余的图片进行排版,直到所有图片都处理完毕。此时所有行的总高度和就是这 N 张图片的排版高度。例如再放入11x1, 5x5, 3x4 的图片后,效果如下图所示,总高度为11:
现在由于排版高度过高,图片的先后顺序也不能改变,小明只好从 N 张图片中选择一张删除掉以降低总高度。他希望剩余N-1张图片按原顺序的排版高度最低,你能求出最低高度是多少么?输入:
第一行包含两个整数 M 和 N,分别表示纸张宽度和图片的数量。
接下来 N 行,每行2个整数Wi, Hi,表示第 i 个图大小为 Wi*Hi。对于30%的数据,满足1<=N<=1000
对于100%的数据,满足1<=N<=100000,1<=M, Wi, Hi<=100输出:
一个整数,表示在删除掉某一张图片之后,排版高度最少能是多少。样例输入1:
4 3
2 2
2 3
2 2
样例输出1:
2
思路:要删去一张图片,使高度最小,无非是遍历N张图片,判断第i个图片不选是否拥有更小的高度。
可以分割一下状态,例如第i行中图片j,判断不选图片j的高度,可以由三个状态组成:
①前i-1行的总高度,这是固定的,在遍历过程就可以知道;
②i+1行以后的总高度,这个要怎么得到呢,可以知道,i+1行开头肯定是新的照片k,我从那张照片k开始遍历到最后一张照片,所得的高度一定是确定的,可以设置一个数组t[i]保留i照片以及以后的高度。
③此时不选j,第i行的高度,想要求这个可以定义一个calc函数,实现向行中添加图片,直到添加完全部图片或者宽度已达最大,求出该行的高度(再加上t[i]就成了第i行以及以后所有行的总高度),为了实现calc函数,还得定义一个solve函数,solve函数的目的是判断加了一张图片,该行的宽度和高度变化。
很明显用了动态规划的思想,他有状态转移关系,问题被细分为了多个子问题,把处理全部细分为了处理行。
这种方法适用于一些题目,题目中总体只修改了部分结构,只需要处理那部分被修改的状态,其余的部分可以通过处理得到,视为常量。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int m,n,h[N],w[N],t[N];
void solve(int i,int& W,int& H){if(W+w[i]<=m){ H=max(H,h[i]); }else{H=max(H,(h[i]*(m-W)+w[i]-1)/w[i]);}W=min(m,W+w[i]);
}
int calc(int i,int W,int H){while(i<n&&W<m)solve(i++,W,H); return H+t[i];
}
int main(){cin>>m>>n;for(int i=0;i<n;i++)cin>>w[i]>>h[i];for(int i=n-1;i>=0;i--)t[i]=calc(i,0,0);int res=t[0],pre_h=0,W=0,H=0;for(int i=0;i<n;i++){int tmp=calc(i+1,W,H);res=min(res,pre_h+tmp);solve(i,W,H);if(W==m)pre_h+=H,W=0,H=0;} cout<<res<<endl;
} 加了注释后:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int m,n,h[N],w[N],t[N];//m为每行最大宽度,n为图片数量,h为每张图片对应高度,w为每张图片对应宽度,t[i]为以i图片为开始,与他以后所有的图片组合,形成的最小高度(一定是以i为行头开始)
void solve(int i,int& W,int& H){//找出加入i元素后,该行的高度和宽度所发生的变化 if(W+w[i]<=m){//没超出最大宽度 H=max(H,h[i]); }else{H=max(H,(h[i]*(m-W)+w[i]-1)/w[i]);//为什么要加w[i]-1,因为他要向上取整,所以要加一个小数,即(w[i]-1)/w[i]}W=min(m,W+w[i]);
}
int calc(int i,int W,int H){//求出加入i以及他后边所有图片后,总高度的变化 while(i<n&&W<m)solve(i++,W,H);//只要算一行的,另起一行的可以直接由t[i]得到 return H+t[i];//为什么这里是H+t[i],因为之前的一行可能已经有照片了,我先填满那一行,拿到那一行的高度即H,然后之后的元素就另起一行了,对应t[i],所以t[i]是需要预处理的,所以总的高度为H+t[i]
}
int main(){cin>>m>>n;for(int i=0;i<n;i++)cin>>w[i]>>h[i];for(int i=n-1;i>=0;i--)t[i]=calc(i,0,0);//W=0,H=0,说明要求的是以i照片开头的,与它以后所有的图片组合形成的最小高度,预处理阶段,不预处理,以后可能有重复的求解过程int res=t[0],pre_h=0,W=0,H=0;//res先取t[0],是代表所有图片都取了后它的高度, pre_h为 之前已经统计了的行的高度,正在统计的不算 for(int i=0;i<n;i++){int tmp=calc(i+1,W,H);//计算出加入i+1以及之后的所有图片后,总高度的变化,不包括i,这就对应了删除一张图片的思想 res=min(res,pre_h+tmp);//前者为之前统计出的最小高度,后者为不要i照片的最小高度 solve(i,W,H);//加入i照片if(W==m)pre_h+=H,W=0,H=0;//此时已经充满一行,那就得另起一行了,所以pre_h要+H,H和W要清零 } cout<<res<<endl;
}