系列文章目录

---

---

前言

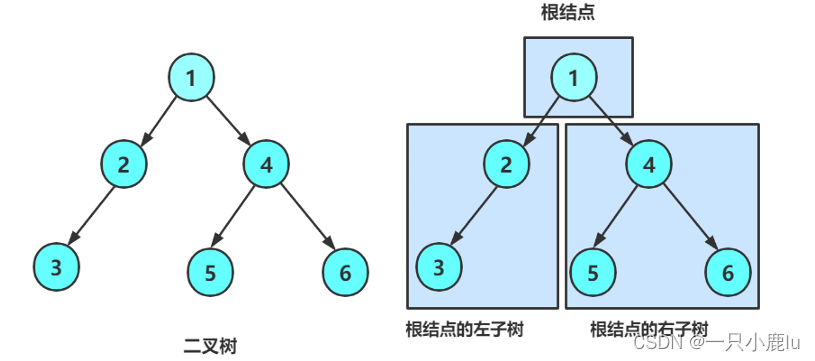
• HashMap 底层是使用了 哈希表（数组实现的哈希表）+ 链表 + 红黑树 实现的，所以学习HashMap的源码，如果对这些数据结构比较了解的话，学习的过程中会有些帮助。

谈一谈HashMap的红黑树节点类 TreeNode 设计

• 为何在学习HashMap之前建议先弄明白 TreeNode 这个类呢，整个 HashMap 最难的就是关于红黑树的一些操作了，所以首先要弄明白他为什么要这么设计，以便后面学习源码时有助于不仅能看懂在干什么，更能明白为什么这么干。
• HashMap 的红黑树 除了维护一般的红黑树的属性像 parent，left，right，color 之外，它还维护了 next 和 prev。所以 HashMap 的红黑树不仅是红黑树还是双向链表。向 TreeMap 中就并没有这样的属性，那么为什么这样设计呢？
• 为了优化红黑树的遍历。直接使用维护的next 即可完成对红黑树的遍历。
• 为什么要遍历红黑树呢，对遍历的顺序有要求吗？
  • 首先要明白 HashMap 不保证数据的有序性，如果是插入到链表上，则是直接追加到链表尾部。
  • 但是在链表转化为红黑树时，红黑树作为二叉平衡搜索树可能是有序的，而且引入红黑树也是为了优化搜索，但是作为链表并不需要有序，而红黑树的有序也是在构建红黑树时，仅仅只针对那一条链表将节点添加到红黑树中做了排序。
  • 所以当红黑树转化为链表时，只需要拿到红黑树的所有节点即可，对遍历的顺序无要求，所以维护了 next可直接获取下一节点，以及在扩容时也可能发生红黑树需要转化为链表的情况。
• 看到这也只是解释了为什么需要维护 next，那么为什么还要维护 prev 呢？
  • 当我们需要查找某个元素时，并且这个元素在红黑树的结构中，那么在红黑树中去寻找某个元素一定得从根节点开始查找，
  • 所以为了提高效率，往往将红黑树的根节点就放在 哈希表中的某个索引位出（后面统称为桶），这个就可直接拿到跟节点。同事也是作为双向链表的头结点。
  • 但是红黑树的平衡调整过程中，可能会发生跟节点的变化，为了将新生成的根节点更新到桶中，则有了 moveRootToFront(tab, root);方法，就是将新的根节点放回桶中，并且更新作为双向链表的头结点，所以链表节点的过程中需要维护链表前后关系，所以需要拿到前一个节点，来与后一个节点进行连接，所以也需要维护 prev。

一、字段分析

	//哈希表初始容量，默认为2^4,包括后面进行扩容，扩容后的容量也一定是 2^n 次方，所以 hash表容量一定是 2^n 次方。//1:为什么一定要是 2 的 n 次方呢？//我在前面的 ArrayDeque集合源码分析 文章中详细解释过，这样设计，可以在取模运算时，使用位运算符号运算，提高效率。//2：为什么取模呢？//后面的源码分析也会提到：因为哈希表是使用数组实现的，取到的模就是数组对应的索引。比如我们往HashMap中添加元素，//肯定需要往哈表中插入，插入前需要确定索引位置，然后就需要对 对key的hash值与 （容量-1） 取模运算，从而得到索引位。static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16//哈希表做大容量，因为 int 取值范围为【-2 ^ 31,2^31 - 1】且 容量必须为 2 的幂次方，所以最大只能是 2^30static final int MAXIMUM_CAPACITY = 1 << 30;//默认的加载因子，与容量相关。当hash表中元素数量超过总容量*加载因子时，则触发扩容。注意：我说的元素数量，不是整个hashMap//已经存储多少个元素，而是单单指使用数组实现的哈希表，有多少个位置已经有元素占用了的数量。static final float DEFAULT_LOAD_FACTOR = 0.75f;//链表转化为红黑树逇阈值，是链表转化为红黑树的条件之一static final int TREEIFY_THRESHOLD = 8;static final int UNTREEIFY_THRESHOLD = 6;//哈表表中的元素至少达到64时，链表可能会转化为红黑树，是链表转化为红黑树的条件之二，两个条件都满足，链表才会转化为红黑树static final int MIN_TREEIFY_CAPACITY = 64;//哈希表，使用Node数组实现，很多地方会称呼每个数组元素位一个个的桶。transient Node<K,V>[] table;//为了方便访问访问？？todotransient Set<Map.Entry<K,V>> entrySet;//存储的数据数量transient int size;//版本号transient int modCount;//用于记录容量阈值， = capacity * loadFactor，超过这个数量则扩容，基本面试过程中大部分人都会这么说，很多面试题也是这么//回答的，但其实并不全面，他还有一个特殊情况下的作用：当我们初始化hashMap,并传入了容量，hashMap 并不会立刻对桶进行初始化//桶还是null，这时候 threshold 记录应该被初始化的容量（也就不等于capacity * loadFactor），在第一次添加元素时，//就会用threshold的值来给桶进行扩容。int threshold;//和 DEFAULT_LOAD_FACTOR 作用一样，只是DEFAULT_LOAD_FACTOR 是默认的，而这是用户设置的看，只会在 HashMap 初始化时//可以传入。final float loadFactor;

二、构造方法分析

//传入桶的初始化容量和加载因子
public HashMap(int initialCapacity, float loadFactor) {//初始容量不可小于0if (initialCapacity < 0)throw new IllegalArgumentException("Illegal initial capacity: " +//同样的初始容量不可移除，最大值 MAXIMUM_CAPACITYif (initialCapacity > MAXIMUM_CAPACITY)initialCapacity = MAXIMUM_CAPACITY;//检查加载因子是否合法if (loadFactor <= 0 || Float.isNaN(loadFactor))throw new IllegalArgumentException("Illegal load factor: " +//赋值加载因子                                       loadFactor);this.loadFactor = loadFactor;//tableSizeFor(initialCapacity): 计算得到 >= initialCapacity 且是2的幂次方的数//所以对于桶并没有进行初始化，还是null，且容量阈值threshold 用来记录下次扩容应该扩容的容量，//在第一次添加元素时会进行用该值进行扩容，并重新计算 threshold，在扩容的方法里有体现：resize()中会有体现this.threshold = tableSizeFor(initialCapacity);}//只指定初始容量
public HashMap(int initialCapacity) {this(initialCapacity, DEFAULT_LOAD_FACTOR);}//无参构造函数，加载因子使用默认值
public HashMap() {this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted}//参数容器 m，获取m中的所有元素添加到HashMap中
public HashMap(Map<? extends K, ? extends V> m) {//使用默认的加载因子this.loadFactor = DEFAULT_LOAD_FACTOR;putMapEntries(m, false);}//m：从m中获取所有元素添加到桶中
//evict：在hashMap中可忽略，是用来做拓展的。比如LinkedHashMap（hashMap的子类）会使用，可以用来删除最久未被使用的元素
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) {//需要遍历集合m的大小int s = m.size();if (s > 0) {//如果桶还未初始化if (table == null) { // pre-size//计算桶应该扩容多大的容量//我们知道，当桶的容量达到了  桶容量 * loadFactory 就会扩容，所以现在已知需要s个元素需要添加//那么我们初始化的桶容量最起码在不需要扩容的情况下装的下，所以是 ((float)s / loadFactor) + 1.0F //后面再 + 1正好是在没到扩容阈值的情况下的最小容量了。float ft = ((float)s / loadFactor) + 1.0F;//检查溢出的情况int t = ((ft < (float)MAXIMUM_CAPACITY) ?(int)ft : MAXIMUM_CAPACITY);//因为桶的容量必须是2的幂次方，但是我们计算得到的t不一定是2的幂次方，所以计算得到 >= t 且是2的幂次方的数，//tableSizeFor方法我在前面的 treeMap 中有详细的推到过程，这里便不再详细解释了。if (t > threshold)threshold = tableSizeFor(t);}//如果说通已经初始化了，检查是否需要扩容else if (s > threshold)resize();//遍历 m 的所有元素，添加到桶中，putVal 过程中会检查桶是否初始化和是否需要扩容for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {K key = e.getKey();V value = e.getValue();//详情可看下面 方法分析中的添加元素方法putVal(hash(key), key, value, false, evict);}}}

三、内部类分析

• 哈希表的节点类：哈希表就是使用该类的数组实现哈希表的，同时也是链表的节点类。

	//哈希表的实现类，也是通过节点实现的相比树的节点，要更加复杂static class Node<K,V> implements Map.Entry<K,V> {//使用 key 计算得出的hash值，用来判断是否和新添加进来的元素发生哈希冲突final int hash;//存储的key，就是我们调用 hashMap.put(key,value)的key，用来计算hash值，还会被用来判断在插入数据到红黑树是，应该//往左子树中插入还是右子树中插入，和一般的搜索树不同的是，一般的搜索树，只需要key来比较即可（所以key一定需要有可比较性），//但是HashMap 中则不同，key 不一定需要具有可比性。final K key;//存储的 valueV value;//链表的头节点，那红黑树呢？红黑树会使用 子类TreeNode 来存储元素Node<K,V> next;Node(int hash, K key, V value, Node<K,V> next) {this.hash = hash;this.key = key;this.value = value;this.next = next;}...}

• 红黑树节点类：当链表转化为红黑树时，原来的Node 节点也会变为 TreeNode 节点。
  • 针对 split（）方法的低位与高位做下额外的解释。
  • 低位节点特征满足：(e.hash & oldCap) == 0（使用位运算才能看出端倪）。
  • 高位节点特征满足：(e.hash & oldCap) != 0（使用位运算才能看出端倪）。
  • 若table[i]桶位上的红黑树，它所有的TreeNode节点恰好符合“低位节点”特征，那么在resize后，会构建一条“低位节点双向链表”；此外这棵红黑树root节点在新表的位置还是i，即newTab[i]=root，而且红黑树无需调整。
  • 若table[i]桶位上的红黑树，它所有的TreeNode节点恰好符合“高位节点”特征，那么在resize后，会构建一条“高位节点双向链表”；此外这棵红黑树root节点在新表的位置i+oldCap，即newTab[i+oldCap]=root，而且红黑树无需调整。
  • 若table[i]桶位上的红黑树它所有的TreeNode节点中，既有“高位节点”又有“低位节点”，这时spit方法真正起效了，此时红黑树会被spit成一条“低位节点双向链表”和一条“高位节点双向链表”
  • 低位节点双向链表的头部节点位于newTab[i]上，若该链表长度大于6，将基于该双向链构建一棵红黑树；若长度<=6，则将该双向链表变成单向链表。
  • 高位节点双向链表的头部节点位于newTab[i+oldCap]上，若该链表长度大于6，并基于该双向链构建一棵红黑树；若长度<=6，则将该双向链表变成单向链表。

static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {TreeNode<K,V> parent;  // red-black tree linksTreeNode<K,V> left;TreeNode<K,V> right;TreeNode<K,V> prev;    // needed to unlink next upon deletionboolean red;TreeNode(int hash, K key, V val, Node<K,V> next) {super(hash, key, val, next);}/*** Returns root of tree containing this node.*/final TreeNode<K,V> root() {for (TreeNode<K,V> r = this, p;;) {if ((p = r.parent) == null)return r;r = p;}}//确保 root为 桶中的节点，不是则更新为是 static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {int n;if (root != null && tab != null && (n = tab.length) > 0) {int index = (n - 1) & root.hash;TreeNode<K,V> first = (TreeNode<K,V>)tab[index];//整个过程为：// rp-><- root -><- rn//rp-><- root -> rn, rp <- rn;//rp <- root -> rn, rp -><- rn;//root  <- first//root -> first//null <- root;//=>  null  <- root -><- first  ,rp-><- rn;//其实就是更新下root为头结点，将root从链表顺序的关系中拿出来放到 first 的前面，并没有改变//红黑树的结构，移动的时候要维护双向链表的性质即next和previf (root != first) {Node<K,V> rn;tab[index] = root;TreeNode<K,V> rp = root.prev;if ((rn = root.next) != null)((TreeNode<K,V>)rn).prev = rp;if (rp != null)rp.next = rn;if (first != null)first.prev = root;root.next = first;root.prev = null;}//验证红黑树的五条性质是否都满足assert checkInvariants(root);}}//从调用该方法的节点出发，寻找与给定 k 相等的节点//参数k的哈希值//参数k的 calss类型 final TreeNode<K,V> find(int h, Object k, Class<?> kc) {//从掉用该方法的节点出发，p：表示当前遍历到的节点TreeNode<K,V> p = this;do {//ph：记录节点 p 的hash值//dir：记录p的key与参数 k 的比较结果。 1：p的key < k  ； 0：相等； -1:p的key > k://pk：记录节点p 的keyint ph, dir; K pk;//pl：记录节点p左节点//pr：记录节点p右节点TreeNode<K,V> pl = p.left, pr = p.right, q;//在寻找过程中，判断是去左子树找，还是去右子树去找，在无法比较出大小的情况下是会经历很多次比较的。//而 hash 是最优先用来比较的，如果直接能比较出大小最好，后面不用比了，直接知道了需要去左还是右//节点p的hash > h，则去左子树继续查找if ((ph = p.hash) > h)p = pl;// 小于则去右子树查找else if (ph < h)p = pr;//到这里说明 p的hash 和 给定的h 相等，则使用k来比较是否就是我们需要找的元素    else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;//到这里说明hash值相等，但是key不相等，先判断左右是否为空，如果乙方为空，坑定只有去不为空的一方了，所以不用比    else if (pl == null)p = pr;else if (pr == null)p = pl;//如果左右子树不为空，且hash值相等但是key不行等，则改用key来比较应该去哪边。    else if ((kc != null ||(kc = comparableClassFor(k)) != null) &&(dir = compareComparables(kc, k, pk)) != 0)p = (dir < 0) ? pl : pr;//如果到这里说明kc== null || k比较==0，没办法，只能将左右两边都找一遍。。//递归从右边找    else if ((q = pr.find(h, k, kc)) != null)return q;else//右边没找到，则迭代从左边开始找p = pl;} while (p != null);//未找到返回nullreturn null;}//查找整颗树中节点的key = k 的节点并返回final TreeNode<K,V> getTreeNode(int h, Object k) {//既然是从整棵树上找，那当然是从根节点roo开始找了，然后调用 root.findreturn ((parent != null) ? root() : this).find(h, k, null);}//该方法为TreeNode 的内部方法。//树化操作，table 为传入的桶final void treeify(Node<K,V>[] tab) {//用于记录根节点TreeNode<K,V> root = null;//x:记录当前表里到的节点，从根节点开始（this）就是根节点，该方法是用root.treeify()来调用的//next：记录下一次访问的节点for (TreeNode<K,V> x = this, next; x != null; x = next) {//更新下一次要访问的节点next = (TreeNode<K,V>)x.next;//将当前节点的左右子节点设为空x.left = x.right = null;//第一次循环，更新跟节点if (root == null) {x.parent = null;//红黑树中的根节点为黑色x.red = false;root = x;}else {//不是第一次for循环了//记录当前节点的 kK k = x.key;//记录当前节点 hash值int h = x.hash;//记录当前节点 key 所属的 classClass<?> kc = null;//从红黑树的根节点开始遍历，判断当前节点应该插入到红黑树的哪个位置for (TreeNode<K,V> p = root;;) {//dir 记录单签节点应该插入到红黑树的左子树还是右子树// dir = 1:表示新插入节点应该插入到当前节点的左子树中。// dir = 0:表示新插入节点应该插入到当前节点的右子树中。//dir = -1:表示新插入节点的hash值和当前节点的hash值相等，//需要进一步比较新插入节点的key和当前节点的key。//ph：用于记录当前遍历到的红黑树节点p的hash值int dir, ph;//记录当前遍历到的红黑树节点p 的keyK pk = p.key;//先使用新节点和当前节点p的hash进行比较if ((ph = p.hash) > h)dir = -1;else if (ph < h)dir = 1;//到这里新的节点和节点 的 hash值相等。//1：comparableClassFor获取k的calss//2：compareComparables尝试使用两个节点的key的//compareto方法执行（前提是实现了Compareable接口，但可能没实现，//也可能实现了比较后是相等。。）else if ((kc == null &&(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0)//来带这里说明两个hash值相等，两个key Class不同，或者pk == null 或者两个key//调用compareTo后还是相等，则进一步比较//tieBreakOrder：先用他们的 classname比较，还是相等则最后使用他们的内存地址比较dir = tieBreakOrder(k, pk);//记录下要插入位置的父节点TreeNode<K,V> xp = p;//如果要插入的位置没有节点了，则说明该位置就是我们要插入的位置if ((p = (dir <= 0) ? p.left : p.right) == null) {//新插入节点指向 xpx.parent = xp;//判断是否插父节点xp的左边还是右边if (dir <= 0)xp.left = x;elsexp.right = x;//插入后调成红黑树的平衡，并返回根节点。红黑树的平衡调整并不在说明了，//在前面的 TreeMap中也有红黑树的平衡调整，代码几乎一样，有兴趣可以看我的//那篇 TreeMap源码分析root = balanceInsertion(root, x);break;}}}}//最后确认我们得到的root是否是在桶中的，即红黑树的根节点就是存储在桶中的。//因为可能有并发操作，导致桶发生变化，比如 resizemoveRootToFront(tab, root);}//将红黑结构转化为链表结构，红黑树的根节点会调用此方法//再删除元素的过程中，如果删除的是红黑树上的节点，被删除后红黑树的节点数量 <=6 则会触发 //从这里也体现出 TreeNode 中维护额外的字段 next 和 prev （即双向链表）的好处，在红黑树转化为链表是变得非常//方便高效，只选换成链表节点，在使用TreeNode 的next连接下即可！！final Node<K,V> untreeify(HashMap<K,V> map) {//hd：记录链表的头结点  head//tl：记录链表的尾节点  tailNode<K,V> hd = null, tl = null;//遍历红黑树，右了next是不是遍历非常方便for (Node<K,V> q = this; q != null; q = q.next) {//将 红黑树节点 转化为链表节点Node<K,V> p = map.replacementNode(q, null);//维护单向链表if (tl == null)hd = p;elsetl.next = p;tl = p;}//返回链表的头节点return hd;}//向红黑树中添加节点，只处理添加，不处理覆盖，如果找到相同key，则返回找到的节点让调用者去处理（可能覆盖，可能直接忽略）//插入成功则返回null//map：当前map//tab：当前桶//k：需要被添加节点的k//v：需要被添加节点的value//h：需要被添加节点k的hash值final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,int h, K k, V v) {//用来记录k的calss类型Class<?> kc = null;//向红黑树插入的过程中，我们需要判断是去左子树还是右子树去查找，但是当我们用 hash和key无法判断出去哪边//查找时应该插入到哪个节点下面时，search就等于 = false表示未找到，则会用没办法的办法，//将两边都找下，直到找到合适的boolean searched = false;//先找到红黑树的根节点TreeNode<K,V> root = (parent != null) ? root() : this;//开始从根节点开始遍历，找到应该插入到哪个节点的下面for (TreeNode<K,V> p = root;;) {//dir：记录 hash 或key的比较结果//ph：记录遍历到的节点的hash//pk：记录遍历到的节点的keyint dir, ph; K pk;//优先使用hash比较if ((ph = p.hash) > h)dir = -1;else if (ph < h)dir = 1;//hash相等的情况下开始使用 key 比较,如果相等则说明确实key一样，返回找到的节点else if ((pk = p.key) == k || (k != null && k.equals(pk)))return p;//如果key不相等，则继续比较出应该去左子树找还是去右子树找// comparableClassFor ：获取k的 class//compareComparables：尝试使用两个key在都实现Campareable接口的情况下的，它的compareTo方法比较else if ((kc == null &&(kc = comparableClassFor(k)) == null) ||(dir = compareComparables(kc, k, pk)) == 0) {//到这里说明hash相等，equals不相等，说明p不是要找的节点，但是还是无法值到应该去左子树还是去右子树//所以只能左子树和右子树都尝试找下，直到找到合适的位置或者相同key的节点if (!searched) {TreeNode<K,V> q, ch;searched = true;if (((ch = p.left) != null &&(q = ch.find(h, k, kc)) != null) ||((ch = p.right) != null &&(q = ch.find(h, k, kc)) != null))return q;}//到这里说明确实没有key相同节点，但是又不知道新节点应该插入到左子树中还是右子树中//则使用者最终的方法了，使用两个key的内存地址进行比较！！dir = tieBreakOrder(k, pk);}//记录新节点应该插入到哪个节点后面TreeNode<K,V> xp = p;//如果我们遍历到了节点的度为1或者0，说明到了该插入的时候了 if ((p = (dir <= 0) ? p.left : p.right) == null) {//因为我们插入新节点还是维护链表关系，即按插入的先后时间循序，所以获取//xpn，就是作为链表结构中的下一个节点Node<K,V> xpn = xp.next;TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);if (dir <= 0)xp.left = x;elsexp.right = x;xp.next = x;x.parent = x.prev = xp;if (xpn != null)((TreeNode<K,V>)xpn).prev = x;moveRootToFront(tab, balanceInsertion(root, x));return null;}}}//从红黑树删除当前节点，因为该方法是 通过 treeNode.removeTreeNode来调用的，谁调用删除谁//map：使用map里的replacementNode将红黑树节点转化为链表节点//tab：用于红黑树转化为链表是需要多红黑树中的节点重新调整到桶中，//movable前面介绍过了。final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,boolean movable) {//记录桶的容量int n;//如果同为空直接返回即可if (tab == null || (n = tab.length) == 0)return;//拿到被删除节点（即当前节点）在桶中的索引位    int index = (n - 1) & hash;//先取出index桶位的头节点first，同时first节点也是红黑树的root根节点，因此也有root=first,//rl是root节点的左子节点TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;//由于调用removeTreeNode的节点就是一个TreeNode，因此其next节点就是后继节点赋给succ变量，//prev节点为前驱节点赋给pred变量TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;// 如果当前节点node的前驱节点为空,说明前节点node就位于桶位头节点上，因为要删除当前节点node，//故只需将将first指向succ，并将当前节点node的后继节点succ放入桶位上，就可完成“删除当前节点node”的操作//  node(头节点) <=> succ <=> succ.next  变成 succ(头节点) <=> succ.nextif (pred == null)tab[index] = first = succ;else//前驱节点不为空：pred<=> node <=> succ <=> succ.next 变成 pred -> succ <=> succ.nextpred.next = succ;//如果后继节点不为空：pred -> succ <=> succ.next 变成 pred <=> succ <=> succ.next，if (succ != null)succ.prev = pred;// 前面可知tab[index] = first = succ，如果first为空，也即succ为空，说明本次删除节点已经完成，//对于这种情况，删除当前节点node，其实tab[index]=null，也即该桶位为空了，//就不需要做删除之后的平衡操作或者树转链表从中，可直接返回。if (first == null)return;if (root.parent != null)root = root.root();//1:只有一个root节点，且空节点//2:root.right == null，说明只有一个左子节点，因此从红黑树性质可知：此时树只有两个节点：根节点root（黑色）、//左子节点（红色）//3:若root.right == null不成立，则来到条件：(rl = root.left) == null，它成立说明左子节点为空，//且只有一个右子节点，由于红黑树性质可推导出：此时树只有两个节点：根节点root（黑色）、右子节点（红色）//4:若root.right == null不成立，(rl = root.left) == null不成立，也即根节点有左右子节点，//则来到条件rl.left == null，它成立则说明此时红黑树也是一棵简单的红黑树且构成有多种形式，//但红黑树约束性质可知：基本对应到有2到6个节点//最多6的情况，少于该情况就需要转链表//                A （黑）//           A （黑）        A（黑）    //             A （红）   A（红）   A（红）if (root == null || root.right == null ||(rl = root.left) == null || rl.left == null) {tab[index] = first.untreeify(map);  // too smallreturn;}//红黑树节点超过6个对应的删除逻辑。以上操作将被删除节点从链表结构中删除了，接下来将在作为红黑树的结构中删除//这一部分可以说和Treemap中红黑树删除节点的逻辑一模一样，只是对于不同情况讨论的顺序不一样，可看看我 TreeMap//的源码分析和删除后对于红黑树的平衡调整的分析。TreeNode<K,V> p = this, pl = left, pr = right, replacement;if (pl != null && pr != null) {TreeNode<K,V> s = pr, sl;while ((sl = s.left) != null) // find successors = sl;boolean c = s.red; s.red = p.red; p.red = c; // swap colorsTreeNode<K,V> sr = s.right;TreeNode<K,V> pp = p.parent;if (s == pr) { // p was s's direct parentp.parent = s;s.right = p;}else {TreeNode<K,V> sp = s.parent;if ((p.parent = sp) != null) {if (s == sp.left)sp.left = p;elsesp.right = p;}if ((s.right = pr) != null)pr.parent = s;}p.left = null;if ((p.right = sr) != null)sr.parent = p;if ((s.left = pl) != null)pl.parent = s;if ((s.parent = pp) == null)root = s;else if (p == pp.left)pp.left = s;elsepp.right = s;if (sr != null)replacement = sr;elsereplacement = p;}else if (pl != null)replacement = pl;else if (pr != null)replacement = pr;elsereplacement = p;if (replacement != p) {TreeNode<K,V> pp = replacement.parent = p.parent;if (pp == null)root = replacement;else if (p == pp.left)pp.left = replacement;elsepp.right = replacement;p.left = p.right = p.parent = null;}TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);if (replacement == p) {  // detachTreeNode<K,V> pp = p.parent;p.parent = null;if (pp != null) {if (p == pp.left)pp.left = null;else if (p == pp.right)pp.right = null;}}//判断是否需要将新的根节点转移到桶的索引位处if (movable)moveRootToFront(tab, r);}        //map:当前hashMap对象//tab：新桶，即库容后的新桶//当前节点在旧桶中的索引位//旧桶容量//整个方法是将index处的红黑树从旧桶移动到新桶tab上final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {//当前节点，即旧桶中的节点，也是index处的红黑树的根节点TreeNode<K,V> b = this;// Relink into lo and hi lists, preserving order//和链表从旧桶移动到新桶的逻辑是一样的//loHead：记录低位的红黑树的头结点，loTail：记录低位的红黑树尾结点TreeNode<K,V> loHead = null, loTail = null;//hiHead：记录高位的红黑树的头结点，hiTail：记录高位的红黑树尾结点TreeNode<K,V> hiHead = null, hiTail = null;//lc：低位红黑树的节点数量//hc：高位红黑树的节点数量int lc = 0, hc = 0;//开始从当前节点b开始遍历红黑树//e:当前遍历到红黑树节点，next 为下一个要遍历的节点for (TreeNode<K,V> e = b, next; e != null; e = next) {//更新下一个将要遍历得到节点next = (TreeNode<K,V>)e.next;//没遍历一个节点，将它指向下一个节点的引用断开e.next = null;//当前节点为低位的情况，插入到低位红黑树中if ((e.hash & bit) == 0) {//如果是第一次插入到节点到低位，则也更新下头结点为eif ((e.prev = loTail) == null)loHead = e;else//否则用低位尾结点的下一位指向当前节点eloTail.next = e;//更新尾结点    loTail = e;++lc;}else {//处理高位的情况if ((e.prev = hiTail) == null)hiHead = e;elsehiTail.next = e;hiTail = e;++hc;}}//将低位的红黑树插入到新桶中去if (loHead != null) {//如果新的红黑树节点太少了 <= 6 ，将红黑树转化为链表if (lc <= UNTREEIFY_THRESHOLD)tab[index] = loHead.untreeify(map);else {//否则直接插入并进行树化操作tab[index] = loHead;if (hiHead != null) // (else is already treeified)loHead.treeify(tab);}}//一样的操作，将高位的红黑树插入到新桶中去if (hiHead != null) {if (hc <= UNTREEIFY_THRESHOLD)tab[index + bit] = hiHead.untreeify(map);else {tab[index + bit] = hiHead;if (loHead != null)hiHead.treeify(tab);}}}...

四、方法分析

• 添加元素方法

//添加元素
public V put(K key, V value) {//继续调用添加元素方法，参数含义下面会介绍return putVal(hash(key), key, value, false, true);}    
//使用key 计算 hash值并返回
//1：如果 key 为null放入下标为0的桶位置
//2：否则调用 key 对象自己的hashCode方法，无论你传入的key对象的hashCode如果和谐，为了保证hash值更具有唯一性，
//将得到的hash，让hash 的高十六位 与 低十六位进行混合，所以用的^运算，让 得到的hash每一位都参与了混合运算，
//增加了混合性和散列性，降低了冲突的概率。
static final int hash(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);}
//参数介绍：
//hash ： 使用key计算得到的hash值，
//key ：将要添加的元素 key
//value ： 将要添加的元素 value
//onlyIfAbsent：如果为true：只有 key 不存在时才会插入，否则本次不插入也不覆盖。false：不管键存不存在都插入（就是不存在肯定插入了，如果存在会覆盖value，注意：只覆盖value）。
//evict：如果为true：必要时会会删除最老的节点，LinkedHashMap会使用，HashMap中并未用到。
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {//记录hash表Node<K,V>[] tab;//一开始是：记录要插入的位置，该位置上已存在的节点（hash冲突），//后来:到了需要再链表中遍历查找合适的位置时，变成 e 记录当前节点，p记录e的前一个节点。Node<K,V> p; //n：记录桶的数组的长度int n, i;//哈希表中没有元素，当前是第一次插入元素if ((tab = table) == null || (n = tab.length) == 0)//重新计算容量，并记录容量，用于取模运算：(n - 1) & hashn = (tab = resize()).length;if ((p = tab[i = (n - 1) & hash]) == null)//tab[i = (n - 1) & hash]：计算出应该插入的桶位置，因为容量为2的幂，所以(n - 1) & hash 等价于 hash % n//将该位置插入新的节点，因为是该位置的第一个节点，所以没有指向下一个节点next的值，所以掺入nulltab[i] = newNode(hash, key, value, null);else {//执行到这里，说明发生了Hash冲突！！//e：表示当前节点的引用，在循环遍历过程中会不断更新。 k：当前节点的 k，通俗点就是已经占用了相同位置的那个节点。//以便在查找过程中去比较 k 来判断是插入新的节点还是覆盖。//当然，如果是红黑树，还会用来比较去左子树中去找，还是右子树去找Node<K,V> e; K k;//用来判断新添加的节点key 是否和已存的节点的key 是否相等。因为相等的话会覆盖。//p.hash == hash：首先 比较两个使用key计算得到的hash值，只有hash值相等才有必要继续走 && 后面的判断。//但是不同的key是有可能得到相同的hash的，所以继续判断：//((k = p.key) == key || (key != null && key.equals(k))) : 为什么 == 和 equals 都判断下呢？？//因为HashMap 也不知道你传入的key是基本数据类型想 123，还是引用类型，如new User（），为了都兼顾到，所以//使用了 == 和 equals 都判断下，满足其一即可。if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))e = p;else if (p instanceof TreeNode)//已存在桶位置的节点是红黑树的节点，那么就把新节点插入到红黑树中e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);else {//已存在桶位置的节点是单链表的节点，那么就把新节点插入到链表中//死循环，直到直到应该插入到合适的位置即可，当然，链表的遍历过程中，可能发现某个节点的key和新节点是相同的//则也是进行覆盖，否则插入for (int binCount = 0; ; ++binCount) {//更新当前遍历到的节点e，并判断是否为空//如果为空，说明该位置就是我要插入的位置，p是上一个节点，直接插入即可。if ((e = p.next) == null) {p.next = newNode(hash, key, value, null);//插入过后，判断是否需要将链表转化为红黑树//这里分析下到底是链表中需要多少节点才会转换？？//第一次执行for循环式 bingCount = 0 且 e = p.next == null，桶位置的节点是头部节点，所以算一个//所以bincount = 某位置链表节点数量（包括桶位置的头部节点） - 1；//所以 binCount >= (TREEIFY_THRESHOLD - 1 = 7) // =>  某位置链表节点数量（包括桶位置的头部节点） - 1 >= 7// => 某位置链表节点数量（包括桶位置的头部节点） >= 8//所以是 >= 8 才可能触发链表转化为 红黑树！！但是！！这时候新节点会插入进来呢，所以准确的说法是：//链表已存在8个节点，第9个节点插完后可能会触发转化为红黑树，为什么说可能呢？？//因为在 treeifyBin 方法里还会对整个桶的容量判断，当！容量！ 》= 64 时，则会触发链表转红黑树//注意我的用词，是容量，不是你整个HashMap存储的所少个元素（即size）也不是整个桶实际有多少桶已经被//使用的数量，而是！！整个桶的容量！！！即 table.lengthif (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1sttreeifyBin(tab, hash);break;}//如果遍历过程中发现 key 判断后已存在，同样的进行覆盖。只覆盖value，不覆盖keyif (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))break;p = e;}}//新传入节点的key 和 已存在节点的key 相等if (e != null) { // existing mapping for keyV oldValue = e.value;//onlyIfAbsent ：前面介绍过，//如果为true：只有 key 不存在时才会插入，否则本次不插入也不覆盖。//所以我们常用的 hashMap.put()，就是如果 key已存在则覆盖，且仅覆盖value，这点需要注意，并不覆盖key//其中可以在上面的判断if (!onlyIfAbsent || oldValue == null)e.value = value;//该方法是一种拓展方法，在HashMap 中是空的，并没有具体逻辑处理，那么它的作用是什么呢？//是为了那些利用HashMap来存储数据，但是每次访问某个元素时，需要额外做一些工作，是一种拓展。//比如 LinkedHashMap 就是用HashMap 来存储元素的元素的，但是实现了 afterNodeAccess 方法，他会将刚刚//访问的节点e，移至最末尾 tail 处，表示最近访问的元素，所以对于 LinkedHashMap 来说，越靠近头部的元素节点，//是越久未被访问，所以 LinkedHashMap 可直接用来实现 LRU 算法。HashMap中 该方法忽略。afterNodeAccess(e);//返回被覆盖的值return oldValue;}}//版本 + 1++modCount;//判断是否需要扩容，threshold：分段分析介绍过。if (++size > threshold)resize();//同样的是用于扩展，HashMap 没有逻辑处理。同样的比如 LinkedHashMap 会删除最久未被使用的节点（即头结点）。afterNodeInsertion(evict);return null;}//可能将链表转化为红黑树，能来到这里说明链表的长度已经 >= 8 了//tab：当前桶//hash：新插入节点的hash值final void treeifyBin(Node<K,V>[] tab, int hash) {//n：记录容量//index：记录桶中的索引位//e：记录遍历链表时，当前获取到的节点int n, index; Node<K,V> e;//如果当前桶为空 或 桶的容量 < 64,则会进行扩容，扩容会尝试把每个链表拆成两个链表，插入到扩容后的新桶中//详细可看扩容代码分析。if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)resize();//如果链表节点数量 >= 8 && 桶容量 >= 64 则将链表转化为红黑树   //e = tab[index = (n - 1) & hash 拿到根节点else if ((e = tab[index = (n - 1) & hash]) != null) {//整个过程是将链表的所有节点都转化为 TreeNode，并节点在记录在链表中的顺序，//prev指向红黑树节点在链表中的上个节点//next指向红黑树节点在链表中的下个节点//记录好原先的顺序后方便进行树化操作//hd：记录遍历链表的头结点//tl：记录遍历链表的尾结点TreeNode<K,V> hd = null, tl = null;do {//将当前遍历拿到的节点转化为红黑树的节点TreeNode<K,V> p = replacementTreeNode(e, null);//更新头结点if (tl == null)hd = p;else {//不停地将p给链接上p.prev = tl;tl.next = p;}//更新尾结点tl = p;} while ((e = e.next) != null);//按理说执行到这不可能为null了，但是并发情况下可能出现，所以在检查下if ((tab[index] = hd) != null)//树化操作//hd为红黑树的根节点,可看TreeNode内部类的treeify方法详解。hd.treeify(tab);}}

• 删除元素方法：

//根据key删除
public V remove(Object key) {//记录被删除的节点，并返回该节点的valueNode<K,V> e;return (e = removeNode(hash(key), key, null, false, true)) == null ?null : e.value;}//删除节点
//hash：要删除key的hash值
//key：要删除的key
//value：如果指定了matchValue参数为true，则要删除节点的值需要与此参数匹配，才会将该节点删除。即key和value都要相等才删除。
//matchValue：是否需要匹配节点的值
//movable：用于红黑树中，节点被删除了，可能导致根节点变化，movable= true是，则更新 新的根节点为桶中的节点，否则不更新。
//如果已知删除节点的位置会很频繁地发生变化，设置movable参数为false可能会更有效。
final Node<K,V> removeNode(int hash, Object key, Object value,boolean matchValue, boolean movable) {//记录桶                       Node<K,V>[] tab;//记录可能是被删除的节点Node<K,V> p;//n:记录容量//index：记录可能被删除的节点在桶中的索引位int n, index;//桶不为null && 桶的容量 >0 && 根据传入的key计算出的索引为在桶中是有元素的if ((tab = table) != null && (n = tab.length) > 0 &&(p = tab[index = (n - 1) & hash]) != null) {//node：记录确定被删除的节点//e：记录将要查找的下一个节点//k：记录将要查找的下一个节点的key//v：记录将要查找的下一个节点的valueNode<K,V> node = null, e; K k; V v;//如果可能被删除的节点p的hash、key 都和传入的key和hash一样，p就是我们要删除的节点，更新给nodeif (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))node = p;//p不是我们要删除节点，获取到下一个节点else if ((e = p.next) != null) {//如果要进行查找的是红黑树if (p instanceof TreeNode)//直接从根节点p出发，去查找被删除的节点node = ((TreeNode<K,V>)p).getTreeNode(hash, key);else {//如果要进行链表的查找do {//使用刚刚得到的p的下一个节点e来开始比对//同样的判断if (e.hash == hash &&((k = e.key) == key ||(key != null && key.equals(k)))) {node = e;break;}//否则继续遍历链表查找//p用来记录被找到的节点node的父节点了p = e;} while ((e = e.next) != null);}}//如果我们找到了要删除的节点node，if (node != null && (!matchValue || (v = node.value) == value ||(value != null && value.equals(v)))) {//如果被删除的节点是从红黑树中删除                 if (node instanceof TreeNode)//从红黑树中去删除节点，里面除了会调整平衡外，开可能会触发红黑色再次转化成链表的情况，详情//可看TreeNode内部类此方法介绍((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);else if (node == p)//如果被删除的节点是连边的头部更新，更新新的头部到桶中tab[index] = node.next;else//否则直接点删除p.next = node.next;//版本 + 1++modCount;//元素个数 -1 --size;//用于扩展，hashmap没有逻辑实现。afterNodeRemoval(node);return node;}}return null;}

五、扩容分析

• HashMap没有提供缩容的方法，一方面有实现难度，另一方面有可以完全替代的策略，可以新建一个HashMap 传入 需要缩容的 HashMap 即可，所以没有实现的必要。

//对桶进行扩容
final Node<K,V>[] resize() {//记录当前桶，便于创建新桶后，将旧桶上所有值循环遍历，全部移动到新桶上。新桶：扩容后的桶。Node<K,V>[] oldTab = table;//记录旧桶的容量，为什么 oldTab == null要判断下 null 呢，因为 hashMap 的初始化时并不会//对桶初始话化（可以看下HashMap构造函数），还是null，第一次//开始添加元素才会对桶初始化，所以就是为了应对这种情况的。int oldCap = (oldTab == null) ? 0 : oldTab.length;//记录旧桶的阈值int oldThr = threshold;//newCap:记录新桶的容量//newThr：记录新桶的阈值，因为阈值 = 容量 * 负载因子int newCap, newThr = 0;//说明旧桶容量 > 0,则继续判断是否需要扩容了if (oldCap > 0) {//如果旧桶的容量 已经大于所能给的最大容量了，抱歉，已经扩容到最大了，无法在继续扩容了，所以返回就得旧桶了，尽力局。if (oldCap >= MAXIMUM_CAPACITY) {threshold = Integer.MAX_VALUE;return oldTab;}//否则的话可以进行扩容//newCap = oldCap << 1：将旧的容量扩容为两倍，赋给新的容量//(newCap = oldCap << 1) < MAXIMUM_CAPACITY：判断扩容后的容量是否超过在大容量，超过了，后面会给你纠正//过来，给到你最大值 MAXIMUM_CAPACITY //oldCap >= DEFAULT_INITIAL_CAPACITY：新的容量是否 >= 8//所以：扩容后既不能超过最大容量 && 旧的容量 >=8 ,才会给你按 2倍进行扩容。else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&oldCap >= DEFAULT_INITIAL_CAPACITY)newThr = oldThr << 1; // double threshold}//执行到这里说明旧的容量 <=0, 用来处理特殊情况的，在我们调用HashMap构造方法并传入了容量：new HashMap（10）,//hashmap并不会设置去设置初始化桶，桶还是空的，只有开始添加元素，才会初始化桶。//但是会用 阈值threshold记录应该被初始化的容量。else if (oldThr > 0) // initial capacity was placed in thresholdnewCap = oldThr;else {               // zero initial threshold signifies using defaults//执行到这里说明 oldCap <= 0,且初始化HashMap时并没有传入指定容量，所以使用默认最小容量//并且计算下阈值newCap = DEFAULT_INITIAL_CAPACITY;newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);}//如果新的阈值为0，就是为了处理上面 else if (oldThr > 0) 这种情况，需要重新计算阈值if (newThr == 0) {//计算阈值float ft = (float)newCap * loadFactor;//计算后的阈值不能溢出了！！最大只能给到  Integer.MAX_VALUEnewThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?(int)ft : Integer.MAX_VALUE);}//更新hashmap的阈值threshold = newThr;//使用新的容量创建新桶啦，不用想，后面肯定是一些列将旧桶的元素全部移动到新桶上的操作，事实上也确实如此。Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];//更新hashMap的桶为新桶table = newTab;//看看旧桶有没有元素，针对初始化时没有给桶初始化，所以旧桶==null的特殊情况if (oldTab != null) {//开始遍历旧桶啦for (int j = 0; j < oldCap; ++j) {//用于记录每次便利拿到的旧桶上的节点Node<K,V> e;//hashMap 的桶不能保证所有位置都有元素，所以判断下，没值的话肯定不用移动了//e 拿到了当前旧桶遍历到的元素if ((e = oldTab[j]) != null) {//将旧桶便利到的位置设为空，方便后面垃圾回收oldTab[j] = null;//下面开始判断拿到的节点是链表还是红黑树，//如果仅仅只有一个节点，直接用新的容量计算下索引位置即可if (e.next == null)newTab[e.hash & (newCap - 1)] = e;else if (e instanceof TreeNode)//如果j位置不仅仅是一个节点，而是一个红黑树的根节点，按理说，我把根节点移动到新的桶中不就可以了嘛？//那你可就想的太简单了，首先哈希冲突有两种，一种 是真的不同的key计算到的hash值相同，还有一种是计算//到的hash值不同，但是取模运算得到桶的下标位置却相同，现在好了，扩容了，当然需要将这些红黑树数上的//节点一个一个重新计算在桶的位置。而且数组的元素查找是复杂度是O(1)，红黑树是O(logn),而且还有左右//节点，颜色等属性开销，所以为了性能，也要重新计算。//详细操作过程我在下面的split（）方法中详细介绍了。todo((TreeNode<K,V>)e).split(this, newTab, j, oldCap);else { // preserve order//j位置的桶不止一个节点，还是一个链表，先从整体上说明下处理流程://j位置原桶中是一个链表，下面会尝试拆成两个链表，我们称呼为低位链表和高位链表，符合服务旧链表//中的每个节点到新的两个链表中呢？？//如果旧链表的节点&oldCap == 0，则被分配到低位链表去，而loHead 用于记录低位链表的头部// loTail 同于记录低位链表尾部//如果旧链表的节点&oldCap != 0，则被分配到高位链表去，而hiHead 用于记录高位链表的头部// hiTail 同于记录高位链表尾部。//直到旧链表节点遍历完（即next == null），将新生成的两个链表插入到新的桶中Node<K,V> loHead = null, loTail = null;Node<K,V> hiHead = null, hiTail = null;//用于记录链表中，下一个将要被访问的节点，直到旧链表访问完Node<K,V> next;do {//更新下一个将要被访问节点next = e.next;//为何使用 (e.hash & oldCap) == 0 来判断低位和高位呢？//旧的桶造成hash冲突可能是 计算的hash值不同，但是取余运算时，结果计算的位置却一样，//所以使用该方法可以减少这种情况//分配给低位链表if ((e.hash & oldCap) == 0) {if (loTail == null)loHead = e;elseloTail.next = e;loTail = e;}else {//分配给高位if (hiTail == null)hiHead = e;elsehiTail.next = e;hiTail = e;}} while ((e = next) != null);//将新生成的低位链表插入到新的桶中if (loTail != null) {loTail.next = null;//索引位和旧桶一致newTab[j] = loHead;}//将新生成的高位链表插入到新的桶中if (hiTail != null) {hiTail.next = null;//位置为：旧索引 + 旧桶容量newTab[j + oldCap] = hiHead;}}}}}//返回新桶return newTab;}

六、总结

• 本文章主要针对 HashMap 的数据结构 TreeNode 设计，添加元素，删除元素，扩容，红黑树转链表，链表转红黑树等方法做了详细的介绍分析。

参考资料：

小破栈上的小码哥HashMap讲解
HashMap中针对高位与低位的理解