矩阵乘法
知阵乘法是《线性代数》中的基础内容,但在考察数学的算法题中也会出现。
本节我们学习基础的矩阵乘法规则。
每个矩阵会有一个行数和一个列数,只有当相乘的两个矩阵的左矩阵的列数等于右矩阵的行数
时,才能相乘,否则不允许做矩阵乘法。
例如,3x5的矩阵可以和5x7的矩阵做乘法,但是3x5的阵不能和4x7的矩阵做乘法N*M的知阵利M*K的矩阵做乘法后的矩阵大小为N*K
矩阵乘法的规则用一句话描述就是,第一个矩阵A的第i行和第二个矩阵B的第i列的各M个元素对应相乘再相加得到新矩阵C[i][j]的值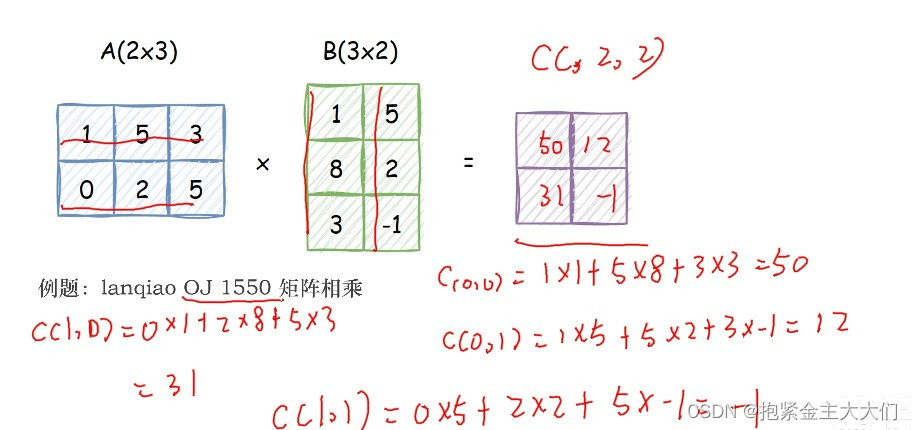
例题
矩阵相乘
题目描述
小明最近刚刚学习了矩阵乘法,但是他计算的速度太慢,于是他希望你能帮他写一个矩阵乘法的运算器。
输入描述
输入的第一行包含三个正整数 N,M,K,表示一个 $NM的矩阵乘以一个的矩阵乘以一个MK的矩阵。接下来N行,每行M个整数,表示第一个矩阵。再接下来的M行,每行K$ 个整数,表示第二个矩阵。
0<<N,M,K≤100, 0≤ 矩阵中的每个数 ≤1000
输出描述
输出有 N 行,每行 K 个整数,表示矩阵乘法的结果。
输入输出样例
示例
输入
2 1 3
1
2
1 2 3
输出
1 2 3
2 4 6package shuxeu;
import java.util.*;
public class juzhen {public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);int m=scan.nextInt();int n=scan.nextInt();int k=scan.nextInt();int [][]a=new int[m][n];int [][]p=new int[n][k];for(int i=0;i<m;i++) {for(int j=0;j<n;j++) {a[i][j]=scan.nextInt();}}for(int i=0;i<n;i++) {for(int j=0;j<k;j++) {p[n][k]=scan.nextInt();}}int[][]sum=new int[m][k];for(int i=0;i<m;i++) {for(int j=0;j<k;j++) {for(int c=0;c<n;c++) {sum[i][j]+=a[i][c]*p[c][j]; }System.out.println(sum[i][j]);}System.out.println("");}}}