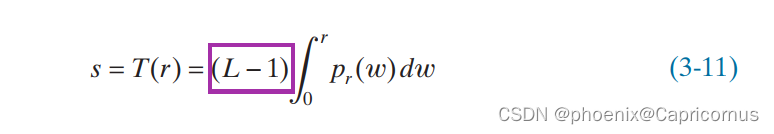108.将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入： nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入： nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• $1\le nums.length\le 10^4$
• $-10^4\le nums[i]\le 10^4$
• nums 按 严格递增 顺序排列

解法一(递归+模拟)

思路分析：

1. 根据二叉搜索树的特点，左子树节点小于中间节点，且右子树节点大于中间节点
2. 且题目给出数组为严格递增序列，且要求构造的二叉搜索树是 高度平衡的二叉搜索树
3. 所以很显然，构造二叉树时，应该将数组中间的数值作为根节点
4. 考虑使用递归的方式构造，首先思考递归的返回值和参数，因为需要获得一个二叉搜索树，所以返回值类型为TreeNode，然后传递的参数，需要有数组参数以及数组的左右节点，确定转化的序列
5. 然后思考递归的边界条件，即当数组的左边界大于右边界时，不需要再构造，返回null
6. 然后确定递归的一般过程，即根据数组左右边界确定构造二叉树的根节点，然后再构造左右子树

实现代码如下：

class Solution {public TreeNode sortedArrayToBST(int[] nums) {return toBSTBySortArray(nums, 0, nums.length-1);	// 注意转递区间为左闭右闭区间}private TreeNode toBSTBySortArray(int[] nums, int left, int right) {if (left > right)return null;	// 说明此时为空数组int rootValIndex = ((right - left) >> 1) + left;	// 获取根节点的索引TreeNode root = new TreeNode(nums[rootValIndex]);root.left = toBSTBySortArray(nums, left, rootValIndex-1);	// 构造左子树root.right = toBSTBySortArray(nums, rootValIndex+1, right);	// 构造右子树return root;}
}

提交结果如下：

解答成功:
执行耗时:0 ms,击败了100.00% 的Java用户
内存消耗:42.1 MB,击败了65.39% 的Java用户

复杂度分析：

• 时间复杂度：$O(N)$，N指数组的长度
• 空间复杂度：$O(lo{g}_2^N)$