曲线降采样之道格拉斯-普克算法Douglas–Peucker
该算法的目的是,给定一条由线段构成的曲线,找到一条点数较少的相似曲线,来近似描述原始的曲线,达到降低时间、空间复杂度和平滑曲线的目的。

附赠自动驾驶学习资料和量产经验:链接
示例(B中红色为降采样后的曲线)

算法流程



4. 此时算法已经完成了一个循环,后续按照递归的方式,分别对线段p1-p6和p6-p7进行同样的处理,p6-p7之间的点已经处理完,则直接结束;距离p1-p6线段最远的点为p5,p5到线段距离大于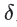 ,则p5也是需要保留的点;
,则p5也是需要保留的点;


5. 同理,p5-p6线段之间无待处理点,直接结束;距离p1-p5线段最远的点为p3,其到线段的距离仍大于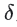 ,则保留p3;
,则保留p3;


6. 距离线段p1-p3最远的点为p2,其距离小于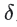 ,将p1到p3中间所有的点标记为忽略;距离线段p3-p5最远的点为p4,其距离也小于
,将p1到p3中间所有的点标记为忽略;距离线段p3-p5最远的点为p4,其距离也小于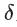 ,将p3-p5之间所有待处理点标记为忽略;
,将p3-p5之间所有待处理点标记为忽略;
7. 至此,算法结束,上述过程中,所有组成线段的端点即为降采样后曲线的点。
时间复杂度
引用:https://zh.wikipedia.org/wiki/%E9%81%93%E6%A0%BC%E6%8B%89%E6%96%AF-%E6%99%AE%E5%85%8B%E7%AE%97%E6%B3%95

代码
-
定义基本结构和工具函数
// 二维点
struct Point2D {
double x;
double y;
Point2D() : x(0.0), y(0.0) {}
Point2D(double x, double y) : x(x), y(y) {}
};// 计算点到线段的距离
double DouglasPeucker::GetDistanceOnLine(const Point2D &start,
const Point2D &end,
const Point2D &point) {
float a = end.y - start.y;
float b = start.x - end.x;
float c = end.x * start.y - start.x * end.y;
return std::fabs(a * point.x + b * point.y + c) / std::sqrt(a * a + b * b);
} -
核心处理函数
std::vector
DouglasPeucker::Process(const std::vector &points_in,
const double delta) {
std::vector result;
// points为需要处理的点集,其中第一个和最后一个点为线段的端点,delta为误差阈值
// step1. 找到距离线段最远的点
double max_dist = -1;
int max_idx = -1;
// 两头的点默认是保留的, 不需要进行计算
for (int i = 1; i < points_in.size() - 1; i++) {
double d = GetDistanceOnLine(points_in[0], points_in[points_in.size() - 1],
points_in[i]);
if (d > max_dist) {
max_dist = d;
max_idx = i;
}
}
// step2. 如果最远点的距离大于阈值,则将其作为新的线段端点,递归处理
if (max_dist > delta) {
std::vector left_pts, right_pts;
left_pts.reserve(max_idx + 1);
right_pts.reserve(points_in.size() - max_idx);
for (int i = 0; i <= max_idx; i++) {
left_pts.push_back(points_in[i]);
}
for (int i = max_idx; i < points_in.size(); i++) {
right_pts.push_back(points_in[i]);
}
std::vector left_result = DouglasPeucker::Process(left_pts, delta);
std::vector right_result =
DouglasPeucker::Process(right_pts, delta);
result.insert(result.end(), left_result.begin(), left_result.end() - 1);
result.insert(result.end(), right_result.begin(), right_result.end());
} else { // 两种情况到这里: 点到线段的最大距离小于阈值,或者只有两个点
result.push_back(points_in[0]);
result.push_back(points_in[points_in.size() - 1]);
}
return result;
} -
运行,将上述p1… p7组成的曲线进行降采样,
int main()
{
std::vectorAD::Point2D points_in;
points_in.push_back(AD::Point2D(0.0, 5.0)); // p1
points_in.push_back(AD::Point2D(1.0, 4.0)); // p2
points_in.push_back(AD::Point2D(2.0, 3.2)); // p3
points_in.push_back(AD::Point2D(3.0, 4.5)); // p4
points_in.push_back(AD::Point2D(4.0, 4.7)); // p5
points_in.push_back(AD::Point2D(5.0, 1.0)); // p6
points_in.push_back(AD::Point2D(7.0, 6.0)); // p7
std::vectorAD::Point2D points_out;
points_out = AD::DownSampling::DouglasPeucker::Process(points_in, 0.5);
for (auto &point : points_out) {
std::cout << "x: " << point.x << ", y: " << point.y << std::endl;
}return 0;
}// 输出
x: 0, y: 5 // p1
x: 2, y: 3.2 // p3
x: 4, y: 4.7 // p5
x: 5, y: 1 // p6
x: 7, y: 6 // p7
算法缺点
-
需要调参,但通常参数也比较好确定;
-
时间复杂度不稳定;
-
自顶向下的递归优化,不一定能保证是全局最优,前面做出的选择会影响后续的结果。






![洛谷P1000超级玛丽游戏题解[Python, Rust, Go]](https://img-blog.csdnimg.cn/direct/cd835ec5e9f541f2a262b47c1625392f.png)