目录
一、朴素算法
二、埃氏筛法
1、与朴素算法对比
2、算法介绍
3、例题即代码实现
一、朴素算法
从素数的定义中可以知道,一个整数n要被判断为素数,需要判断n是否能被2.3.n- 1中的一个整除。只2,3..n- 1都不能整除n,n才能判定为素数,而只要有一个能整除n的数出现,n就可以判定为非素数。
这样的判定方法没有问题,复杂度为0(n)。但是在很多题目中,判定素数只是整个算法
中的一部分,这时候0(n)的复杂度实际上有点大,需要更加快速的判定方法。注意到如果在
2 ~n-1中存在n的约数,不妨设为k,即n%k=0,那么由k*(n/k)=n可知,n/k也是n的一个约数,且k与n/k中一定满足其中一个小于等于sqrt(n)、另一个大于等于sqrt(n)其中sqr(n)为根号n。这启发我们,只需要判定n能否被2, 3,.. sqrt(n)中的一个整除(具中x表示对x向下取整),即可判定n县否为素数。这样的话时间复杂度就位o( sqrt(n))。
代码如下:
bool isprime(int x){for(int i=2;i*i<=x;i++){if(x%i==0){return false;}}return true;
}这里有个东西要注意:c++中sqrt函数是对double类型的函数,但是在实际代码中传进来的一般是一个int类型的数,因此我们在使用时要像下面这样让x乘上一个1.0
int main(){int x;cin>>x;ifprime(sqrt(1.0*x));}二、埃氏筛法
1、与朴素算法对比
上面这个算法在判断一个数是否是素数时时间复杂度优越,但是如果我们这个题目需要得到在这个数范围内所有的素数(素数表)时这个时间复杂度就偏大,即o(nsqrt(n))。
2、算法介绍
因此我们要隆重引入我们新的算法埃氏筛法:
当需要生成一个给定范围内所有素数的素数表时,可以采用更高效的算法来降低时间复杂度。一种常见的方法是使用埃拉托斯特尼筛法(Sieve of Eratosthenes)。
埃氏筛法的时间复杂度O(nlog(log(n))),明显优于逐个判断每个数是否为素数的O(nsqrt(n))复杂度。
埃拉托斯特尼筛法的基本思想是从2开始,依次将每个素数的倍数标记为非素数,直到遍历完整个范围。剩下未被标记的数即为素数。
整理步骤如下:
- 初始化一个布尔数组,表示每个数是否为素数,初始值为True。
- 从2开始遍历到n,对于每个素数p,将其倍数p×k(其中k>1)标记为非素数。
- 遍历完整个范围后,未被标记的数即为素数。
这种方法在生成素数表时能够显著减少时间复杂度,是常用的高效算法之一。
3、例题即代码实现
链接-晴问算法:https://sunnywhy.com/sfbj/5/4/205
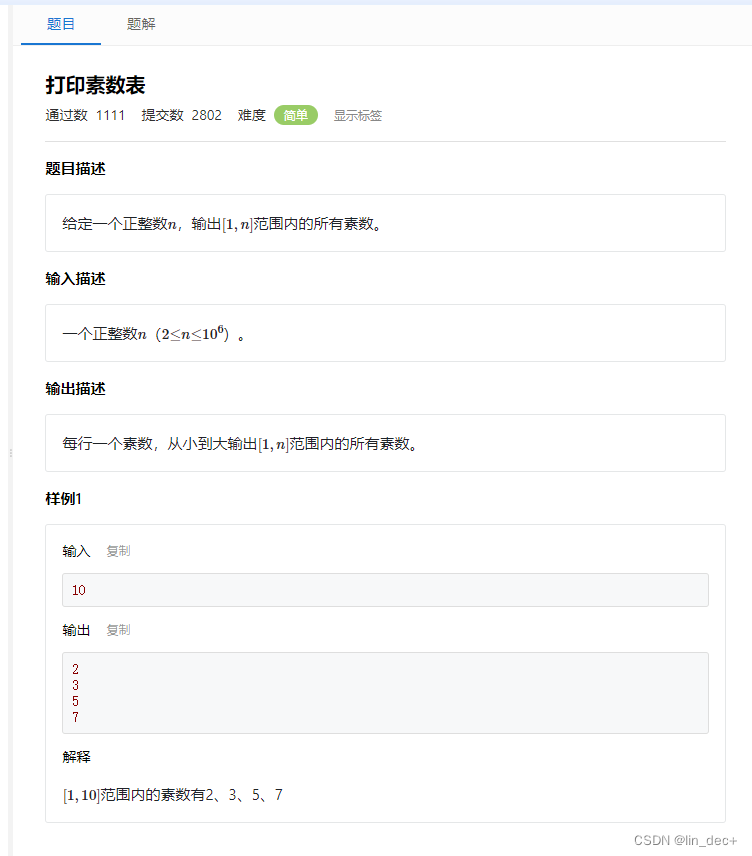
完整ac代码:
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;vector<bool> isprime(n+1,true);for(int i=2;i<=n;i++){if(isprime[i]){for(int j=i+i;j<=n;j+=i){isprime[j]=false;}cout<<i<<endl;}}return 0;
}