题目要找到一个长为k的子串,使得x个相同的k相连长度和s相同且对应字符中只能有一个地方对应的字符不同,

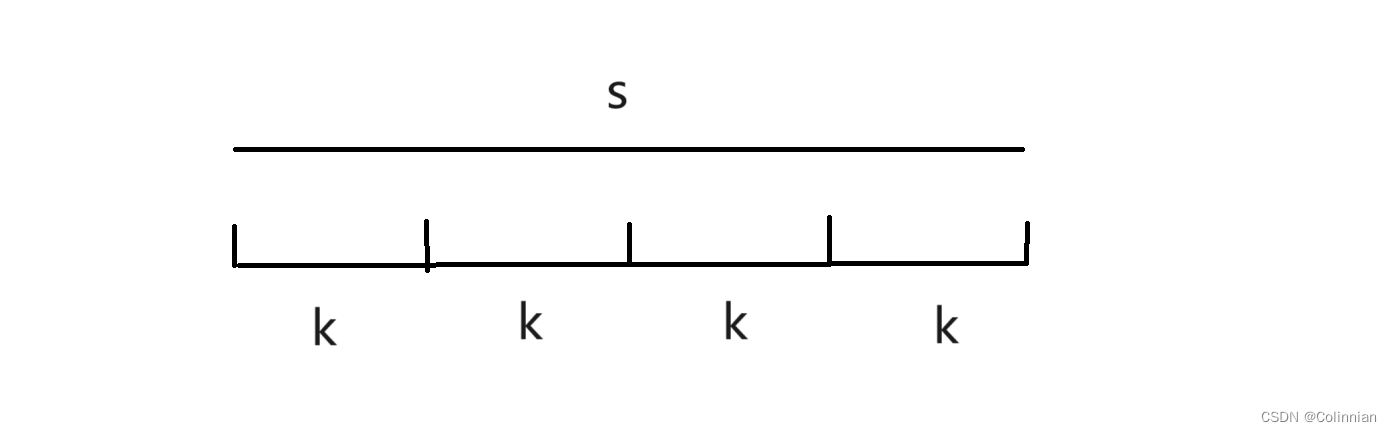
那是不是说明s也能分成x段,且最多有一段中的一个字符不同,否则就不满足要求,那我们现在要讨论这个不同的字符在哪,如果在第一段比如s=abaa aaaa aaaa aaaa,如果我们取了abaa,就会产生abaa abaa abaa,显然这不满足条件,但如果我们选了第二段aaaa,那么就会产生aaaa aaaa aaaa aaaa而这是满足的,长度k也为4,同样是长度为4,选择不同的字段产生的效果是不一样的,那拥有不同字符的那一段不在位置1而在位置2,3,4我们该怎么选,如果在2,我们依旧先选择第一段是否满足,然后再看第二段是否满足,不就好了,如果在三或者4或者5678等,我们只看前两段,必定可以选出不是拥有不同字符的那一段.

也就是说我们只需要避免选出拥有不同字符的那一段即可.

所以解题步骤是枚举k的长度,枚举前两段,按位匹配,记录不同字符的个数

void solve() {int n;std::cin >> n;std::string s;std::cin >> s;//枚举长度for (int len = 1; len <= n; len++) {//找整除的if (n % len != 0) {continue;}//前两段for (int i = 0; i < n && i <= len; i += len) {int ans = 0;//for (int j = 0; j < n; j++) {//每个字符对应模版段的位置ans += (s[i + j % len] != s[j]);}if (ans <= 1) {std::cout << len << "\n";return;}}}
}

F题模拟,我把a或者b伸出来的支称作接口,显然连接一个a消耗一个接口增加两个接口,净增加1,连接b不增加,c要消耗一个,最后构建的二叉树是没有接口的,此外对于最顶端的节点不会消耗接口,所以a,b连接完剩下a+1个接口,c必须要等于a+1,否则不能构建,这很简单,接下来我们看怎样模拟,我们使用队列来模拟,思考一下,最顶端有个接口,它通向第0层,我们先讲0放入队列,然后先匹配a,消耗一个接口0,连接一个a类节点,它的两个接口伸向第一层,所以我们要把两个1放入队列,取出一个1,连接一个a类节点,它的接口伸向第二层,添加两个2到队列里,直到把a连接完.为什么不先连接b呢?思考一下,取出一个b,连接一个b,存入一个b,如果这样连接,每次都会增加一层,这会形成一条垂直的直线,这显然不符合我们的期望,而先连接a可以让每一层能连接的节点数增加.所以我们先连接a再连接b,最后将队列中最后一个取出来,最大的那个数就是层数.

void solve() {int a, b, c;std::cin >> a >> b >> c;if (c != a + 1) {std::cout << -1 << "\n";return;}std::queue<int> q;q.push(0);int ans = 0;while (!q.empty()) {int x = q.front();q.pop();ans = x;if (a) {a--;q.push(x + 1);q.push(x + 1);}else if (b) {b--;q.push(x + 1);}}std::cout << ans << "\n";
}

当然这道题有秒杀公式,但我还没完全理解,这里大家自己看一下吧

void solve() {int a, b, c;std::cin >> a >> b >>c;if (c != a + 1) {std::cout << "-1\n";return;}else {int n = 1;int cnt = 0;while (n - 1 < a) {n *= 2;cnt++;}int t = n - 1 - a;if (b > t)cnt += (b - t + c - 1) / c;std::cout << cnt << '\n';}
}