0. 地球椭圆体

地球表面是一个凸凹不平的表面，而对于地球测量而言，地表是一个无法用数学公式表达的曲面，这样的曲面不能作为测量和制图的基准面。假想一个扁率极小的椭圆，绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体。地球椭球体表面是一个规则的数学表面，可以用数学公式表达，所以在测量和制图中就用它替代地球的自然表面。因此就有了地球椭球体的概念。地球椭球体有长半径和短半径之分，长半径(a)即赤道半径，短半径(b)即极半径。f=（a-b）/a为椭球体的扁率，表示椭球体的扁平程度，a、b、f被称为地球椭球体的三要素。

1. 大地坐标系

大地坐标系（也叫WGS-84坐标系，LLA坐标系，经纬高坐标系，全球地理坐标系)。

任意点都可以描述为经度（Longitude)、纬度（Latitude）和高度(Altitude)，也就是lla坐标。经度(单位${}^o$)是指地球表面上某一点与本初子午线（通常取格林威治子午线）之间的角度，以东经和西经表示。纬度(单位${}^o$)是指地球表面上某一点与赤道之间的角度，以北纬和南纬表示。高度(单位: $m$)或海拔是指某一点相对于参考面（通常是海平面）的垂直距离。

优点: 能够准确地描述地球表面上任意点的位置, 并且可以在地图上直观地表示地球的形状和特征

我们把地球椭球体和基准面结合起来看，在此我们把地球比做是“马铃薯”，表面凸凹不平，而地球椭球体就好比一个“鸭蛋”，那么按照我们前面的定义，基准面就定义了怎样拿这个“鸭蛋”去逼近“马铃薯”某一个区域的表面，X、Y、Z轴进行一定的偏移，并各自旋转一定的角度，大小不适当的时候就缩放一下“鸭蛋”，那么通过如上的处理必定可以达到很好的逼近地球某一区域的表面。

因此，从这一点上也可以很好的理解，每个国家或地区均有各自的基准面，我们通常称谓的北京54坐标系、西安80坐标系实际上指的是我国的两个大地基准面。我国参照前苏联从1953年起采用克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系，1978年采用国际大地测量协会推荐的1975地球椭球体（IAG75）建立了我国新的大地坐标系–西安80坐标系，目前大地测量基本上仍以北京54坐标系作为参照，北京54与西安80坐标之间的转换可查阅国家测绘局公布的对照表。 WGS1984基准面采用WGS84椭球体，它是一地心坐标系，即以地心作为椭球体中心，目前GPS测量数据多以WGS1984为基准。

椭球体与基准面之间的关系是一对多的关系，也就是基准面是在椭球体基础上建立的，但椭球体不能代表基准面，同样的椭球体能定义不同的基准面。地球椭球体和基准面之间的关系以及基准面是如何结合地球椭球体从而实现来逼近地球表面的可以通过下图一目了然。

https://www.whu-cveo.com/2018/07/26/coordinate-projection/

2. eci地心惯性坐标系

，
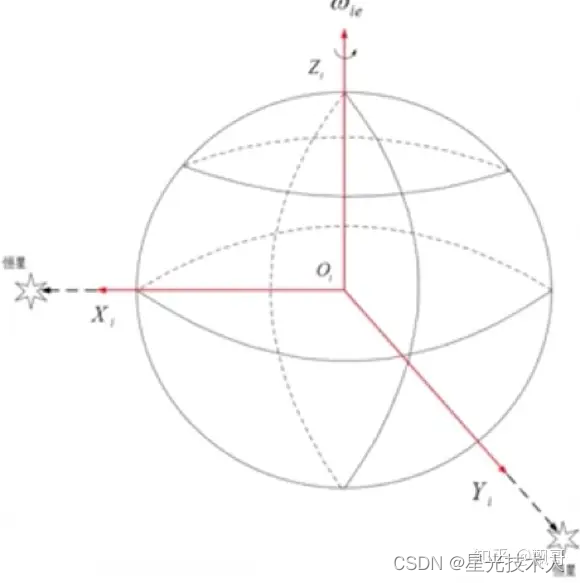
红色O-XYZ坐标系表示地球坐标系，其中低新惯性坐标系（I系）的原点位于地球原点，Z轴沿地轴指向北极，X轴和Y轴位于赤道平面内，满足右手法则，且分别指向两个恒星。
特点：他的特点就是xy不动，不随着地球的自转而转动，可以作为地球附近传感器输出的惯性坐标系。imu检测到或者计算到探测到的加速度，角速度都是相对于地心惯性坐标系的

3. 地心地固坐标系(ECEF坐标系，E系)

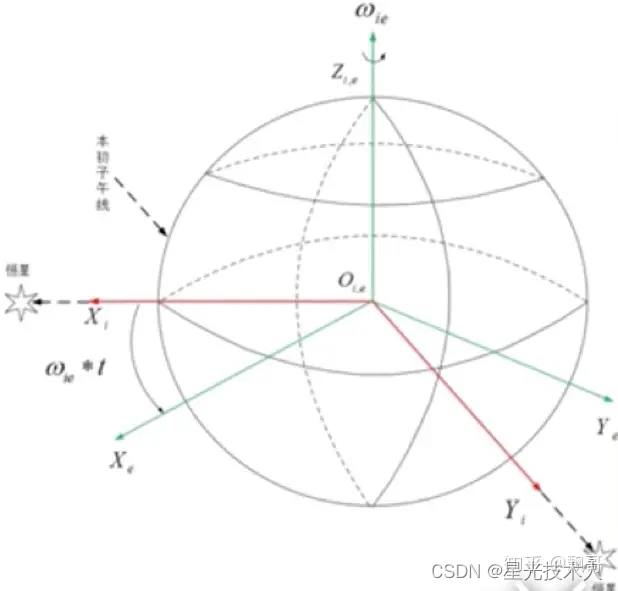
如图，图中绿色$0-xyz$坐标系即为地心地固坐标系（e系），原点位于地球原点，z轴沿着地轴指向北极，y轴沿着赤道平面与格林威治子午面的交线上，y轴在赤道平面与x轴z轴满足右手法则。
特点: 该坐标系与地球固连在一起，x轴和y轴的方向随地球自转而变化

4. 站心坐标系(ENU坐标系)

如图，蓝色的坐标系就是站心坐标系，在北半球被成为ENU坐标系。ENU坐标系的原点位于载体所在的地球表面，x轴和y轴在当地水平面内，分别指向东向和北向，z轴垂直向上，与x轴y轴满足右手法则。
基于地心坐标系的坐标都是很大的值，这样的值是不太方便进行空间计算的，所以很多时候可以选取一个站心点，将这个很大的值变换成一个较小的值。
另外在LLA坐标转化为某坐标系下的三维空间坐标系坐标的时候, 因为距离LLA原点越远，在计算三维坐标的时候距离，距离原点位置越远，误差越大。所以可以选择一个站点坐标系，将待转换的LLA点，转化到这个站点坐标系下，得到的三维空间点位置会比较准确(我的理解：误差原因在于,使用椭圆模型半径和经纬度角度差计算的弧长的时候，距离LLA原点越远，最后得到的弧长误差越大。)

5. LTM坐标系

LTM坐标系是局部切面坐标系（Local Tangent Plane），通常用于描述地球表面上某一点周围的局部地理信息，特别是在地图制作、航空航天、地理勘测、天文观测等领域中常被使用。这个坐标系是相对于某一点（通常是观测点或参考点）建立的局部坐标系，以该点为中心建立的坐标系，可以更准确地描述该点周围的地理位置和方向。

ENU坐标系（East-North-Up）和LTM坐标系（Local Tangent Plane）都是用于描述局部区域的局部坐标系，但它们之间有一些区别：

• 坐标轴方向：
  ENU坐标系的坐标轴方向是东（East）、北（North）和向上（Up）。其中，东方向（E）指的是与地球表面的经线方向平行的方向，北方向（N）指的是与地球表面的纬线方向平行的方向，向上（U）指的是垂直于地球表面向上的方向。
  LTM坐标系的坐标轴方向取决于局部区域的特定情况，它是相对于某一点的局部坐标系。通常情况下，LTM坐标系的坐标轴方向与ENU坐标系的方向是一致的，即东、北和向上。

• 原点选择：
  ENU坐标系的原点可以是任意选择的点，通常选择为局部区域的某个参考点或中心点。
  LTM坐标系的原点也是局部区域的某个参考点或中心点，它是相对于该点建立的局部坐标系。

• 应用领域：
  ENU坐标系常用于导航、飞行控制、地图制作等领域，特别是描述移动物体相对于参考点的位置和方向。
  LTM坐标系常用于地理勘测、航空航天、天文观测等领域，描述局部区域内的地理信息或天文观测点的位置和方向。

• 数学表示：
  ENU坐标系的坐标通常用三维直角坐标表示，即以东、北、向上的分量表示位置。
  LTM坐标系的坐标也是三维直角坐标，通常与ENU坐标系一样以东、北、向上的分量表示位置。
  总的来说，ENU坐标系和LTM坐标系都是用于描述局部区域的局部坐标系，它们的主要区别在于坐标轴方向的定义和应用领域的不同。

项目中，LTM坐标系原点可以设定为项目位置所在的区域的某个位置(LTM系的坐标轴方向一般情况下与ENU坐标系一致)， World系可以定义为系统开机的第一帧IMU位置(方向可以设置为第一帧的姿态，IMU相对LTM系或者ECEF系的姿态，这个具体可以根据需求设定)

6. IMU坐标系

车辆的IMU（惯性测量单元）用于测量车辆的姿态（姿势）信息，包括角速度（角速度测量单位为弧度/秒）和加速度（加速度测量单位为米/秒^2）。IMU可以通过姿态更新算法来估计车辆的姿态，从而实现车身的姿态跟踪（Vehicle Pose Tracking）。

以下是车身IMU的姿态更新原理的基本步骤和算法：

• 数据获取：
  IMU通过其内置的加速度计和陀螺仪获取车辆的角速度和加速度数据。
  角速度数据用于计算车辆在空间中的角度变化，而加速度数据则可以用于辅助姿态估计。

• 姿态估计：
  初始时刻，可以根据IMU的加速度计数据估计车辆的倾斜角（pitch）和侧倾角（roll）。
  姿态估计通常采用互补滤波器（Complementary Filter）或卡尔曼滤波器（Kalman Filter）等算法，结合角速度和加速度数据来估计车辆的姿态。

• 姿态更新：
  姿态更新是指根据IMU获取的最新数据对车辆的姿态进行更新。
  角速度数据可以用于连续地更新车辆的姿态，例如通过积分计算角度变化并更新姿态。
  加速度数据可以用于校准姿态估计结果，例如检测车辆的加速度变化来调整姿态估计的误差。

• 姿态跟踪：
  通过持续的姿态更新，车辆的IMU可以实现对车身姿态的跟踪，包括倾斜角、偏航角等信息。
  姿态跟踪对于车辆的导航、控制和定位非常重要，可以用于实现车辆的姿态稳定控制、路径规划和定位校准等功能。
  总的来说，车身IMU的姿态更新原理基于获取的角速度和加速度数据，结合姿态估计算法和姿态更新算法，持续地更新车辆的姿态信息，从而实现姿态的跟踪和稳定控制。

在实际应用中，可以将开机时第一帧的IMU姿态作为基准姿态或初始姿态（Reference Pose），然后根据后续每一帧的IMU数据计算相对于基准姿态的相对姿态（Relative Pose）或增量姿态（Incremental Pose）。
这种相对姿态的计算通常采用姿态积分（Orientation Integration）的方法，通过累积角速度数据来估计车辆每一时刻的姿态变化。这样可以实现车辆在运动过程中的姿态跟踪，并相对于初始姿态计算出相对的姿态信息。
需要注意的是，姿态积分过程中可能会积累误差，特别是在长时间运行或高动态环境下。为了减小误差的累积，通常会结合其他传感器（如GPS、磁力计等）进行姿态校正或更新，以提高姿态估计的准确性和稳定性。

7. 代码部分

7.1 LLA(大地坐标系坐标、经纬度海拔)坐标转LTM系(ENU系)下的三维笛卡尔坐标

1. 已知LTM坐标系原点的LLA坐标$O_{l}la$、点P为LTM系下的一个点，点P的LLA坐标为$P_{l}la$， 求点P的LTM系坐标$P_{l}tm$

#include <iostream>
#include <cmath>struct LLA {double longitude;double latitude;double altitude;
};struct LTM {double x;double y;double z;
};// Convert LLA to LTM
// 把LLA坐标转化为LTM下的三维笛卡尔坐标
LTM llaToLTM(const LLA& origin, const LLA& point) {const double earthRadius = 6371008.8;  // Earth's radius in metersdouble deltaLongitude = (point.longitude - origin.longitude) * (M_PI / 180.0);double deltaLatitude = (point.latitude - origin.latitude) * (M_PI / 180.0);double x = earthRadius * deltaLongitude * std::cos(origin.latitude * (M_PI / 180.0));double y = earthRadius * deltaLatitude;double z = point.altitude - origin.altitude;return {x, y, z};
}int main() {// LTM坐标系原点对应的LLA坐标LLA origin {115.97040640463173133, 32.328346393150695803, 0.9999999722222 };// LTM系下的四个点的LLA坐标LLA point1 { 115.968928, 32.327075 };LLA point2 { 115.968938, 32.326945 };LLA point3 { 115.9676360, 32.3269011 };LLA point4 { 115.9676295, 32.3270185 };LTM ltmPoint1 = llaToLTM(origin, point1);LTM ltmPoint2 = llaToLTM(origin, point2);LTM ltmPoint3 = llaToLTM(origin, point3);LTM ltmPoint4 = llaToLTM(origin, point4);std::cout << "LTM coordinates of point 1: (" << ltmPoint1.x << ", " << ltmPoint1.y << ", " << ltmPoint1.z << ")\n";std::cout << "LTM coordinates of point 2: (" << ltmPoint2.x << ", " << ltmPoint2.y << ", " << ltmPoint2.z << ")\n";std::cout << "LTM coordinates of point 3: (" << ltmPoint3.x << ", " << ltmPoint3.y << ", " << ltmPoint3.z << ")\n";std::cout << "LTM coordinates of point 4: (" << ltmPoint4.x << ", " << ltmPoint4.y << ", " << ltmPoint4.z << ")\n";return 0;
}

2. 已知LTM坐标系原点的LLA坐标$O_{l}la$，以及自车相对于LLA坐标系的姿态角(roll/pitch/yaw)，点P为LTM系下的一个点，点P的LLA坐标为$P_{l}la$， 求点P的LTM系坐标$P_{l}tm$。

#include <iostream>
#include <cmath>struct LLA {double longitude;double latitude;double altitude;
};struct LTM {double x;double y;double z;
};// Convert degrees to radians
double degToRad(double degrees) {return degrees * (M_PI / 180.0);
}// Convert LLA to LTM
LTM llaToLTM(const LLA& originLLA, const LLA& pointLLA, double roll, double pitch, double yaw) {const double earthRadius = 6371000.0;  // Earth's radius in meters// Convert roll, pitch, and yaw from degrees to radiansdouble rollRad = degToRad(roll);double pitchRad = degToRad(pitch);double yawRad = degToRad(yaw);// Convert LLA to ECEF (Earth-Centered, Earth-Fixed) coordinatesdouble deltaLongitude = (pointLLA.longitude - originLLA.longitude) * (M_PI / 180.0);double deltaLatitude = (pointLLA.latitude - originLLA.latitude) * (M_PI / 180.0);double cosYaw = cos(yawRad);double sinYaw = sin(yawRad);double cosPitch = cos(pitchRad);double sinPitch = sin(pitchRad);double cosRoll = cos(rollRad);double sinRoll = sin(rollRad);double x = deltaLongitude * earthRadius * cos(originLLA.latitude * (M_PI / 180.0)) * cosYaw +deltaLatitude * earthRadius * sinYaw +(pointLLA.altitude - originLLA.altitude) * cosYaw * cosPitch;double y = -deltaLongitude * earthRadius * cos(originLLA.latitude * (M_PI / 180.0)) * sinYaw +deltaLatitude * earthRadius * cosYaw -(pointLLA.altitude - originLLA.altitude) * sinYaw * cosPitch;double z = deltaLongitude * earthRadius * sin(originLLA.latitude * (M_PI / 180.0)) +deltaLatitude * earthRadius * sinPitch +(pointLLA.altitude - originLLA.altitude) * cosPitch;return {x, y, z};
}int main() {LLA originLLA {115.97040640463173133, 32.328346393150695803, 0.9999999722222  };double roll = 0;double pitch = 0;double yaw = 0;LLA point1LLA { 115.968928, 32.327075 };LLA point2LLA { 115.968938, 32.326945 };LLA point3LLA { 115.9676360, 32.3269011 };LLA point4LLA { 115.9676295, 32.3270185 };LTM ltmPoint1 = llaToLTM(originLLA, point1LLA, roll, pitch, yaw);LTM ltmPoint2 = llaToLTM(originLLA, point2LLA, roll, pitch, yaw);LTM ltmPoint3 = llaToLTM(originLLA, point3LLA, roll, pitch, yaw);LTM ltmPoint4 = llaToLTM(originLLA, point4LLA, roll, pitch, yaw);std::cout << "LTM coordinates of point 1: (" << ltmPoint1.x << ", " << ltmPoint1.y << ", " << ltmPoint1.z << ")\n";std::cout << "LTM coordinates of point 2: (" << ltmPoint2.x << ", " << ltmPoint2.y << ", " << ltmPoint2.z << ")\n";std::cout << "LTM coordinates of point 3: (" << ltmPoint3.x << ", " << ltmPoint3.y << ", " << ltmPoint3.z << ")\n";std::cout << "LTM coordinates of point 4: (" << ltmPoint4.x << ", " << ltmPoint4.y << ", " << ltmPoint4.z << ")\n";return 0;
}

辨析:自车在LLA坐标系下的pose和LTM坐标系下的pose辨析
在LLA（经纬度高度）坐标系和LTM（局部切面坐标系）坐标系下，车辆的roll（横滚角）、pitch（俯仰角）和yaw（偏航角）可能有不同的定义和计算方式，具体取决于坐标系的定义和使用场景。

• LLA坐标系下的姿态角：
  在LLA坐标系中，通常roll、pitch和yaw角度是相对于地球表面的经度、纬度和高度来定义的。
  Roll（横滚角）通常指车辆绕其纵轴（对应地球上的经度轴）的旋转角度。
  Pitch（俯仰角）通常指车辆绕其横轴（对应地球上的纬度轴）的旋转角度。
  Yaw（偏航角）通常指车辆绕其竖轴（对应地球上的垂直轴）的旋转角度。

• LTM坐标系下的姿态角：
  在LTM坐标系中，roll、pitch和yaw角度的定义取决于局部坐标系的建立方式和使用场景。
  Roll、pitch和yaw角度通常是相对于LTM坐标系的局部坐标轴来定义的，具体取决于LTM坐标系的建立方式和物体在局部坐标系中的方向。