在 一文中,我们通过了广度优先搜索来得到图结构中各结点的度,
在这一篇文章中,我们要通过深度优先搜索来得到图结构中各结点的度。
初始化
初始化,在下面的代码中,我们创建了一个具有6个结点的图结构,以及使用邻接矩阵来表示图结构。

typedef struct Graph { //创建图结构int values[8][8]; //图结构的邻接矩阵,权值为0意味两结点无路径
} Graph;
void FillGraph(Graph &g) { //初始化出一个随机权值的图结构for(int i =0; i < 8; i++) for(int j = 0; j < 8; j++)g.values[i][j] = 0;g.values[0][1]=1;g.values[1][0]=1;g.values[0][2]=1;g.values[2][0]=1;g.values[1][3]=1;g.values[3][1]=1;g.values[1][4]=1;g.values[4][1]=1;g.values[3][7]=1;g.values[7][3]=1;g.values[4][7]=1;g.values[7][4]=1;g.values[2][5]=1;g.values[5][6]=1;g.values[6][5]=1;g.values[2][6]=1;g.values[5][2]=1;
}//展示图结构中各结点之间的权值
void ShowValues(Graph g) {cout << "Values of each node:" << endl; for(int i = 0; i < 8; i++) {cout<< i << ": ";for(int j = 0; j < 8; j++) {cout << g.values[i][j] << " ";}cout << endl;}cout<<endl;
}
深度优先搜索DFS
深度优先搜索算法(Depth First Search,简称DFS)是一种用于遍历或搜索树或图的算法。
它的基本思想是尽可能深地搜索树的分支,当节点v的所在边都已经被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止
通俗的讲,选定起始结点,随后一条路走到黑(走到没有路径时),返回原路,一旦有路就继续走,如此反复地得到遍历结果。


那么在这个图中,我们若以结点0为起始结点,那么遍历为
0 -> 1 -> 3 -> 7 -> 4 (此时只能再走去结点1,但是1已经遍历过了,因此要进行回溯)
回溯:4 - 7 (结点7没有连接无访问过的结点,因此还得再回溯)
7 - 3, 3 - 1, 1- 0 ,(到达结点0时发现有无访问过的结点2)继续遍历
0 -> 2 -> 5 ->6 (回溯发现所有结点都已访问过,搜索结束)
倘若我们使用路径矩阵,即
int ans[8][8] = {{1, 2}, {3, 4}, {5, 6}, {1, 7}, {1, 7}, {2, 6}, {2, 5}, {3, 4}};
第n个一维数组意味着,结点n连接的结点。如ans[0] = {1, 2} 意味着 结点0 连接 结点1 和 结点2 。
那么我们的代码应当为:
#include <iostream>
#include <queue>
#include <vector>using namespace std;
//图的路径矩阵
vector<vector<int>> adj = {{1, 2}, {3, 4}, {5, 6}, {1, 7}, {1, 7}, {2, 6}, {2, 5}, {3, 4}};
vector<bool> visited;//来记录结点是否被访问过
vector<int> ans; //记录遍历得到的结点,其实也可以省略
int degree[8]; //记录数组的度数void dfsDegree(int v) {ans.push_back(v);visited[v] = true;for (int u : adj[v]) {degree[v]++;if (!visited[u]) {dfsDegree(u);}}
}int main() {visited = vector<bool>(8, false);for (int i = 0; i < 8; i++) {degree[i] = 0;}dfsDegree(0);for (int i : ans) {cout << i << " ";}cout << endl;cout << "DFS to Degrees of each node:" << endl; //输出DFS遍历得到的结果for (int i = 0; i < 8; i++) {cout << "Node " << i << ": " << degree[i] << endl;}cout << endl;return 0;
}
通过运行结果可以得到通过DFS遍历的结果,以及各结点的度数。运行结果如下,
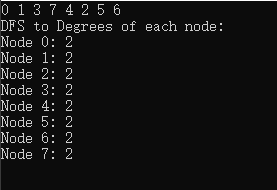
难点在于,如何通过邻接矩阵来进行深度优先遍历。
vector<vector<int>> iadj = {{0,1,1,0,0,0,0,0},{0,0,0,1,1,0,0,0},{0,0,0,0,0,1,1,0},{0,1,0,0,0,0,0,1},{0,1,0,0,0,0,0,1},{0,0,1,0,0,0,1,0},{0,0,1,0,0,1,0,0},{0,0,0,1,1,0,0,0}
};
深度优先遍历的思路是一样的,也就是说我们要修改for循环里面的条件,其他其实不用改动太多。
如通过递归、通过for循环遍历一个结点的相邻结点,判断是否访问过。
不同的是,如果是路径矩阵,for-each循环,得到的u直接就是结点,
而在邻接矩阵,我们如果还是for-each循环,得到的是1,如果要得到结点的话,就需要普通for循环了,用i来记录是哪个结点。
for循环代码为
for(int i = 0; i < 8; i++) {if(adj[v][i] == 0) continue;degree[v]++;if(!visited[i]) dfsDegree(i);}
完整代码如下:
#include <iostream>
#include <queue>
#include <vector>using namespace std;
//图的路径矩阵
vector<vector<int>> adj = {{0,1,1,0,0,0,0,0},{0,0,0,1,1,0,0,0},{0,0,0,0,0,1,1,0},{0,1,0,0,0,0,0,1},{0,1,0,0,0,0,0,1},{0,0,1,0,0,0,1,0},{0,0,1,0,0,1,0,0},{0,0,0,1,1,0,0,0}
};
vector<bool> visited;//来记录结点是否被访问过
vector<int> ans; //记录遍历得到的结点,其实也可以省略
int degree[8]; //记录数组的度数void dfsDegree(int v) {ans.push_back(v);visited[v] = true;for(int i = 0; i < 8; i++) {if(adj[v][i] == 0) continue;degree[v]++;if(!visited[i]) dfsDegree(i);}
}int main() {visited = vector<bool>(8, false);for (int i = 0; i < 8; i++) {degree[i] = 0;}dfsDegree(0);for (int i : ans) {cout << i << " ";}cout << endl;cout << "DFS to Degrees of each node:" << endl; //输出DFS遍历得到的结果for (int i = 0; i < 8; i++) {cout << "Node " << i << ": " << degree[i] << endl;}cout << endl;return 0;
}
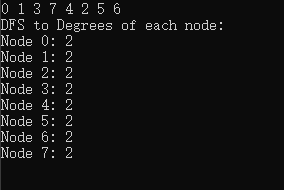
运行结果一致。