😀前言
推荐从上看到下
算法 - 符号表-上

🏠个人主页：尘觉主页

算法 - 符号表

查找树

2-3 查找树引入了 2- 节点和 3- 节点，目的是为了让树平衡。一颗完美平衡的 2-3 查找树的所有空链接到根节点的距离应该是相同的。

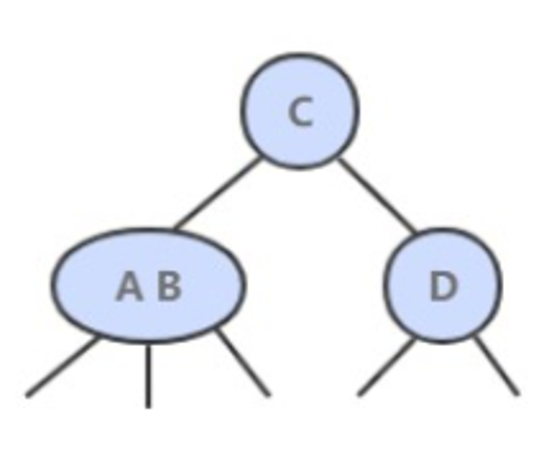
1. 插入操作

插入操作和 BST 的插入操作有很大区别，BST 的插入操作是先进行一a次未命中的查找，然后再将节点插入到对应的空链接上。但是 2-3 查找树如果也这么做的话，那么就会破坏了平衡性。它是将新节点插入到叶子节点上。

根据叶子节点的类型不同，有不同的处理方式：

• 如果插入到 2- 节点上，那么直接将新节点和原来的节点组成 3- 节点即可。

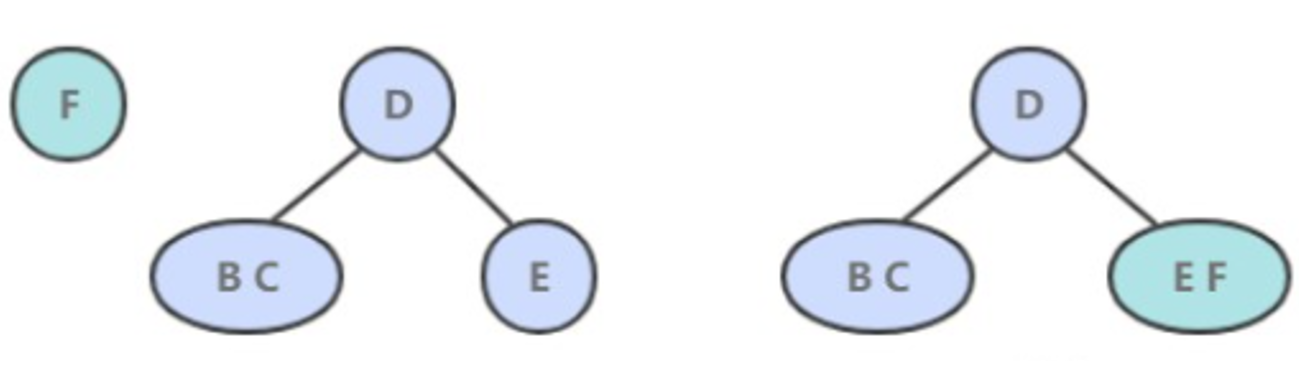
• 如果是插入到 3- 节点上，就会产生一个临时 4- 节点时，需要将 4- 节点分裂成 3 个 2- 节点，并将中间的 2- 节点移到上层节点中。如果上移操作继续产生临时 4- 节点则一直进行分裂上移，直到不存在临时 4- 节点。

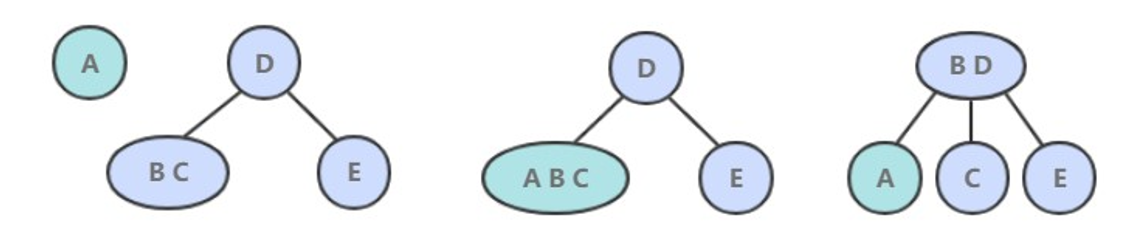
2. 性质

2-3 查找树插入操作的变换都是局部的，除了相关的节点和链接之外不必修改或者检查树的其它部分，而这些局部变换不会影响树的全局有序性和平衡性。

2-3 查找树的查找和插入操作复杂度和插入顺序无关，在最坏的情况下查找和插入操作访问的节点必然不超过 logN 个，含有 10 亿个节点的 2-3 查找树最多只需要访问 30 个节点就能进行任意的查找和插入操作。

红黑树

红黑树是 2-3 查找树，但它不需要分别定义 2- 节点和 3- 节点，而是在普通的二叉查找树之上，为节点添加颜色。指向一个节点的链接颜色如果为红色，那么这个节点和上层节点表示的是一个 3- 节点，而黑色则是普通链接。

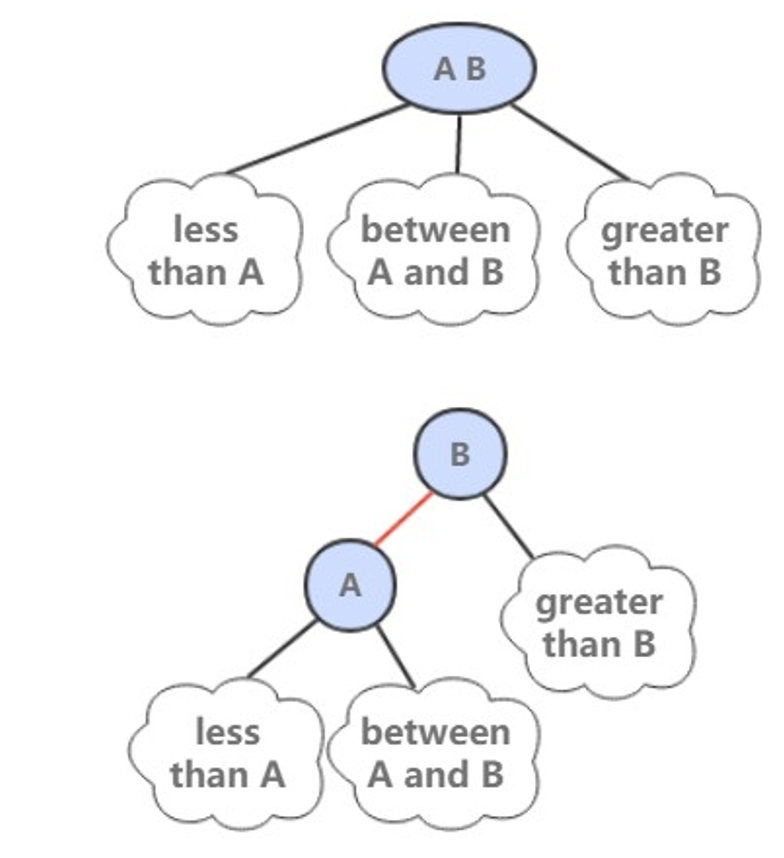
红黑树具有以下性质：

• 红链接都为左链接；
• 完美黑色平衡，即任意空链接到根节点的路径上的黑链接数量相同。

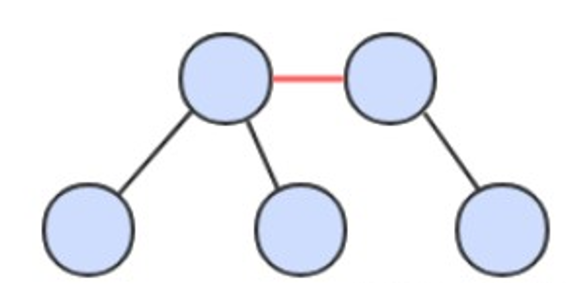
画红黑树时可以将红链接画平。

public class RedBlackBST<Key extends Comparable<Key>, Value> extends BST<Key, Value> {private static final boolean RED = true;private static final boolean BLACK = false;private boolean isRed(Node x) {if (x == null)return false;return x.color == RED;}
}

1. 左旋转

因为合法的红链接都为左链接，如果出现右链接为红链接，那么就需要进行左旋转操作。

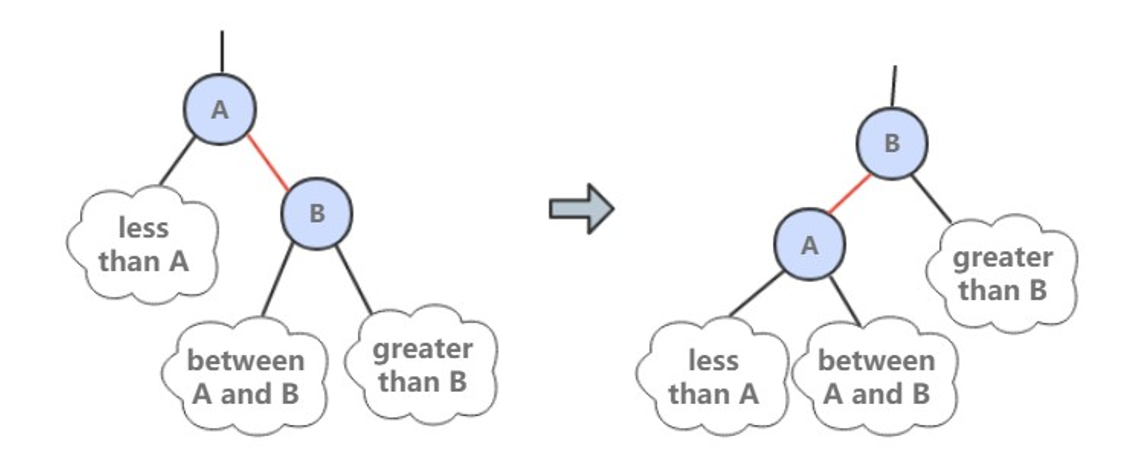
public Node rotateLeft(Node h) {Node x = h.right;h.right = x.left;x.left = h;x.color = h.color;h.color = RED;x.N = h.N;recalculateSize(h);return x;
}

2. 右旋转

进行右旋转是为了转换两个连续的左红链接，这会在之后的插入过程中探讨。

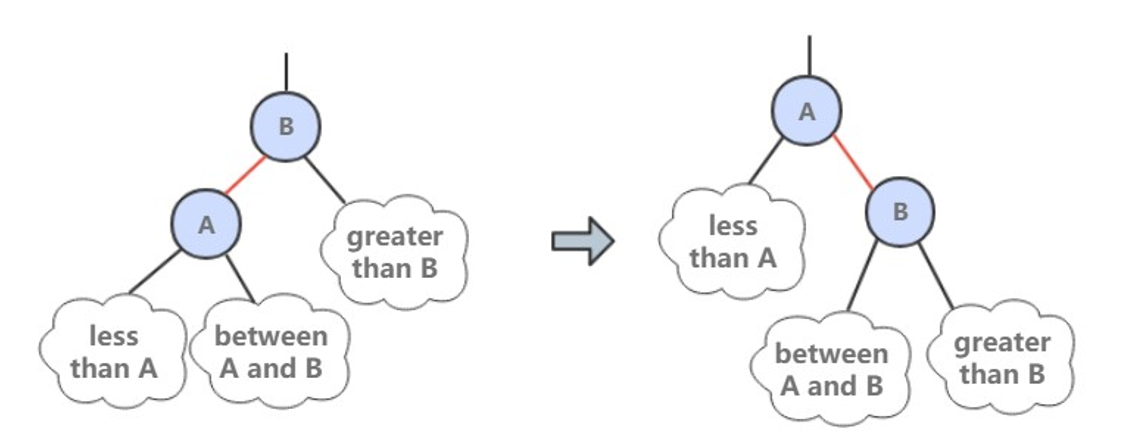
public Node rotateRight(Node h) {Node x = h.left;h.left = x.right;x.right = h;x.color = h.color;h.color = RED;x.N = h.N;recalculateSize(h);return x;
}

3. 颜色转换

一个 4- 节点在红黑树中表现为一个节点的左右子节点都是红色的。分裂 4- 节点除了需要将子节点的颜色由红变黑之外，同时需要将父节点的颜色由黑变红，从 2-3 树的角度看就是将中间节点移到上层节点。

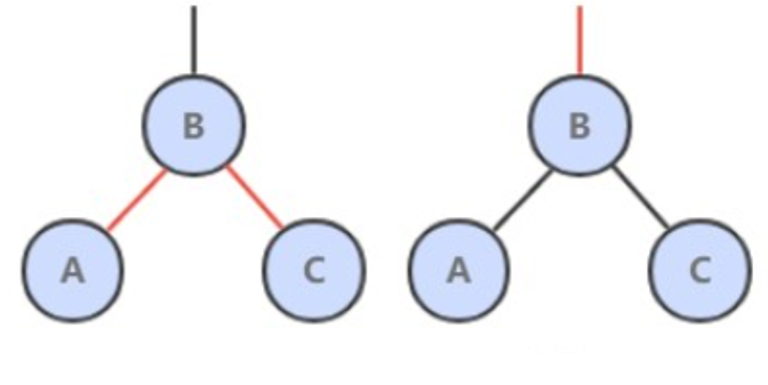
void flipColors(Node h) {h.color = RED;h.left.color = BLACK;h.right.color = BLACK;
}

4. 插入

先将一个节点按二叉查找树的方法插入到正确位置，然后再进行如下颜色操作：

• 如果右子节点是红色的而左子节点是黑色的，进行左旋转；
• 如果左子节点是红色的，而且左子节点的左子节点也是红色的，进行右旋转；
• 如果左右子节点均为红色的，进行颜色转换。

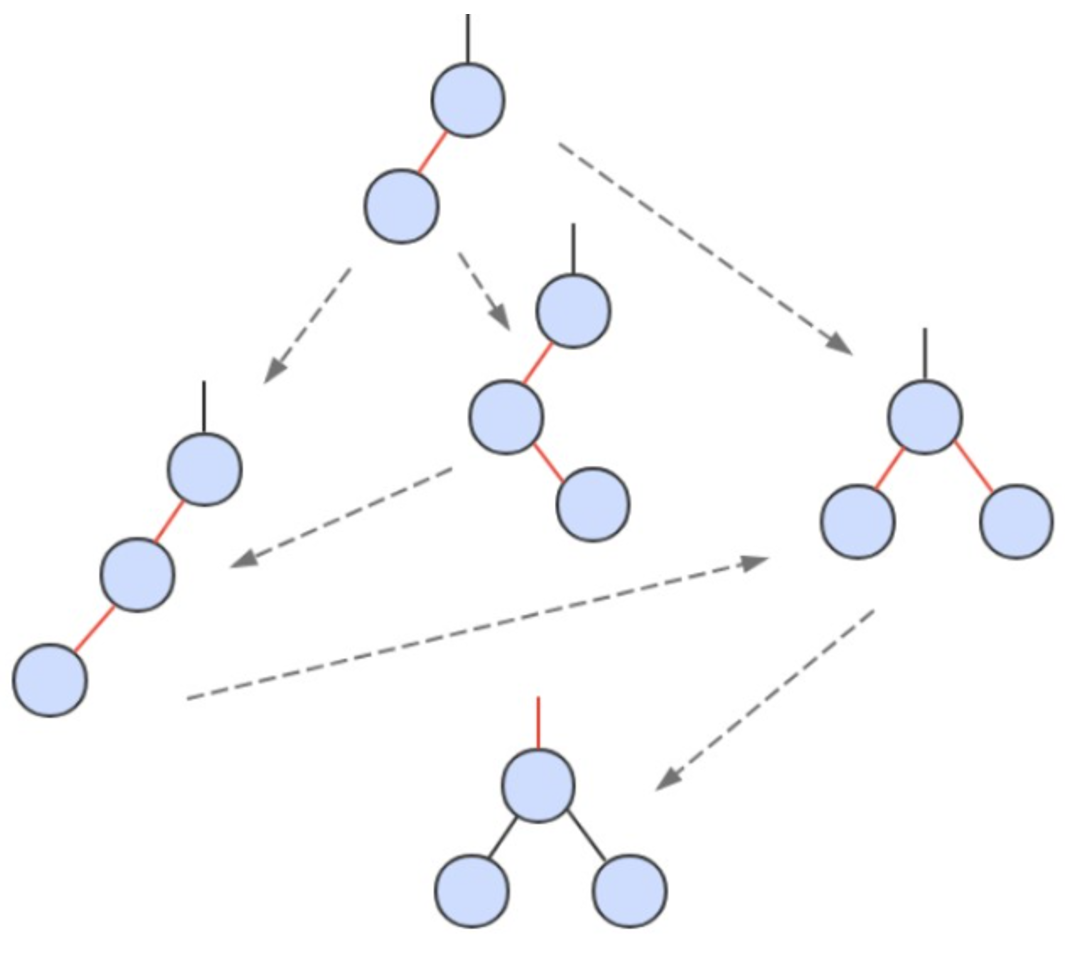
@Override
public void put(Key key, Value value) {root = put(root, key, value);root.color = BLACK;
}private Node put(Node x, Key key, Value value) {if (x == null) {Node node = new Node(key, value, 1);node.color = RED;return node;}int cmp = key.compareTo(x.key);if (cmp == 0)x.val = value;else if (cmp < 0)x.left = put(x.left, key, value);elsex.right = put(x.right, key, value);if (isRed(x.right) && !isRed(x.left))x = rotateLeft(x);if (isRed(x.left) && isRed(x.left.left))x = rotateRight(x);if (isRed(x.left) && isRed(x.right))flipColors(x);recalculateSize(x);return x;
}

可以看到该插入操作和二叉查找树的插入操作类似，只是在最后加入了旋转和颜色变换操作即可。

根节点一定为黑色，因为根节点没有上层节点，也就没有上层节点的左链接指向根节点。flipColors() 有可能会使得根节点的颜色变为红色，每当根节点由红色变成黑色时树的黑链接高度加 1.

5. 分析

一颗大小为 N 的红黑树的高度不会超过 2logN。最坏的情况下是它所对应的 2-3 树，构成最左边的路径节点全部都是 3- 节点而其余都是 2- 节点。

红黑树大多数的操作所需要的时间都是对数级别的。

散列表

散列表类似于数组，可以把散列表的散列值看成数组的索引值。访问散列表和访问数组元素一样快速，它可以在常数时间内实现查找和插入操作。

由于无法通过散列值知道键的大小关系，因此散列表无法实现有序性操作。

1. 散列函数

对于一个大小为 M 的散列表，散列函数能够把任意键转换为 [0, M-1] 内的正整数，该正整数即为 hash 值。

散列表存在冲突，也就是两个不同的键可能有相同的 hash 值。

散列函数应该满足以下三个条件：

• 一致性：相等的键应当有相等的 hash 值，两个键相等表示调用 equals() 返回的值相等。
• 高效性：计算应当简便，有必要的话可以把 hash 值缓存起来，在调用 hash 函数时直接返回。
• 均匀性：所有键的 hash 值应当均匀地分布到 [0, M-1] 之间，如果不能满足这个条件，有可能产生很多冲突，从而导致散列表的性能下降。

除留余数法可以将整数散列到 [0, M-1] 之间，例如一个正整数 k，计算 k%M 既可得到一个 [0, M-1] 之间的 hash 值。注意 M 最好是一个素数，否则无法利用键包含的所有信息。例如 M 为 10^k，那么只能利用键的后 k 位。

对于其它数，可以将其转换成整数的形式，然后利用除留余数法。例如对于浮点数，可以将其的二进制形式转换成整数。

对于多部分组合的类型，每个部分都需要计算 hash 值，这些 hash 值都具有同等重要的地位。为了达到这个目的，可以将该类型看成 R 进制的整数，每个部分都具有不同的权值。

例如，字符串的散列函数实现如下：

int hash = 0;
for (int i = 0; i < s.length(); i++)hash = (R * hash + s.charAt(i)) % M;

再比如，拥有多个成员的自定义类的哈希函数如下：

int hash = (((day * R + month) % M) * R + year) % M;

R 通常取 31。

Java 中的 hashCode() 实现了哈希函数，但是默认使用对象的内存地址值。在使用 hashCode() 时，应当结合除留余数法来使用。因为内存地址是 32 位整数，我们只需要 31 位的非负整数，因此应当屏蔽符号位之后再使用除留余数法。

int hash = (x.hashCode() & 0x7fffffff) % M;

使用 Java 的 HashMap 等自带的哈希表实现时，只需要去实现 Key 类型的 hashCode() 函数即可。Java 规定 hashCode() 能够将键均匀分布于所有的 32 位整数，Java 中的 String、Integer 等对象的 hashCode() 都能实现这一点。以下展示了自定义类型如何实现 hashCode()：

public class Transaction {private final String who;private final Date when;private final double amount;public Transaction(String who, Date when, double amount) {this.who = who;this.when = when;this.amount = amount;}public int hashCode() {int hash = 17;int R = 31;hash = R * hash + who.hashCode();hash = R * hash + when.hashCode();hash = R * hash + ((Double) amount).hashCode();return hash;}
}

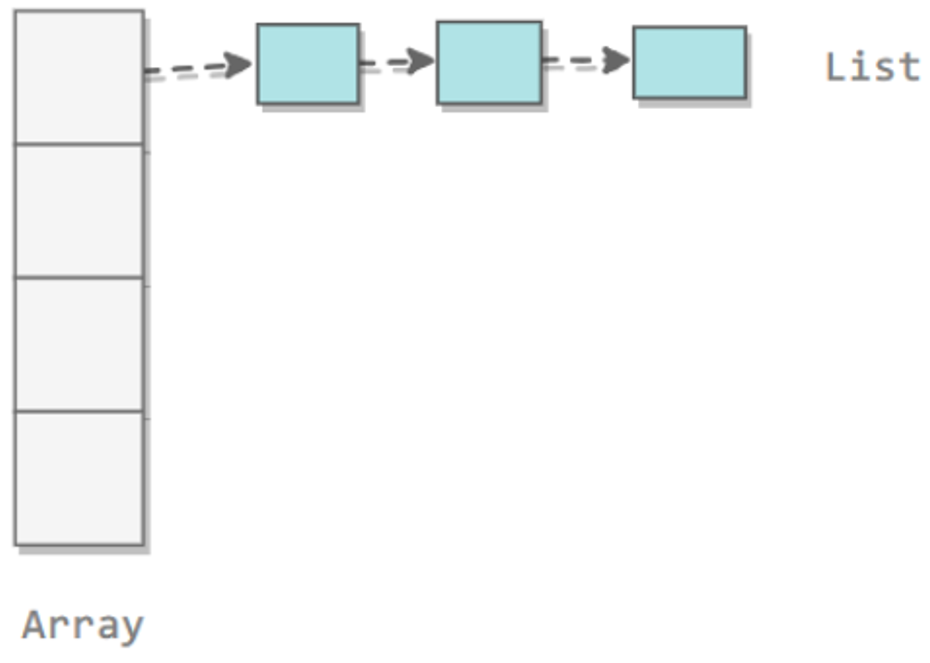
2. 拉链法

拉链法使用链表来存储 hash 值相同的键，从而解决冲突。

查找需要分两步，首先查找 Key 所在的链表，然后在链表中顺序查找。

对于 N 个键，M 条链表 (N>M)，如果哈希函数能够满足均匀性的条件，每条链表的大小趋向于 N/M，因此未命中的查找和插入操作所需要的比较次数为 ~N/M。

3. 线性探测法

线性探测法使用空位来解决冲突，当冲突发生时，向前探测一个空位来存储冲突的键。

使用线性探测法，数组的大小 M 应当大于键的个数 N（M>N)。

public class LinearProbingHashST<Key, Value> implements UnorderedST<Key, Value> {private int N = 0;private int M = 16;private Key[] keys;private Value[] values;public LinearProbingHashST() {init();}public LinearProbingHashST(int M) {this.M = M;init();}private void init() {keys = (Key[]) new Object[M];values = (Value[]) new Object[M];}private int hash(Key key) {return (key.hashCode() & 0x7fffffff) % M;}
}

3.1 查找

public Value get(Key key) {for (int i = hash(key); keys[i] != null; i = (i + 1) % M)if (keys[i].equals(key))return values[i];return null;
}

3.2 插入

public void put(Key key, Value value) {resize();putInternal(key, value);
}private void putInternal(Key key, Value value) {int i;for (i = hash(key); keys[i] != null; i = (i + 1) % M)if (keys[i].equals(key)) {values[i] = value;return;}keys[i] = key;values[i] = value;N++;
}

3.3 删除

删除操作应当将右侧所有相邻的键值对重新插入散列表中。

public void delete(Key key) {int i = hash(key);while (keys[i] != null && !key.equals(keys[i]))i = (i + 1) % M;// 不存在，直接返回if (keys[i] == null)return;keys[i] = null;values[i] = null;// 将之后相连的键值对重新插入i = (i + 1) % M;while (keys[i] != null) {Key keyToRedo = keys[i];Value valToRedo = values[i];keys[i] = null;values[i] = null;N--;putInternal(keyToRedo, valToRedo);i = (i + 1) % M;}N--;resize();
}

3.5 调整数组大小

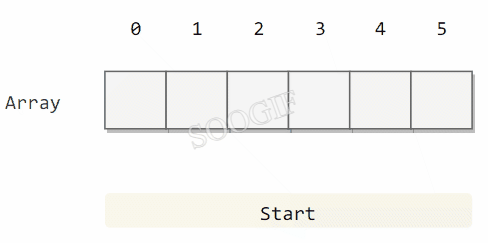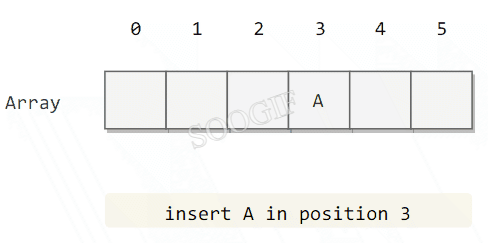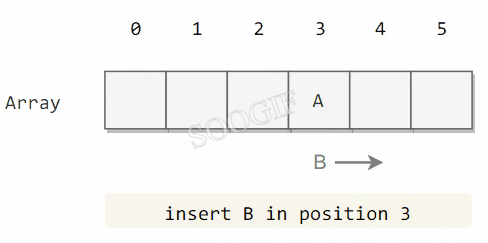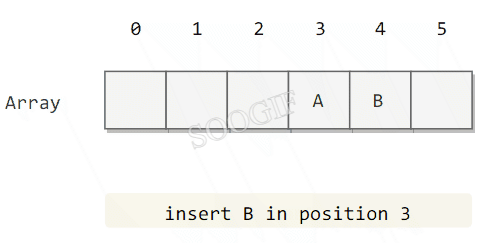
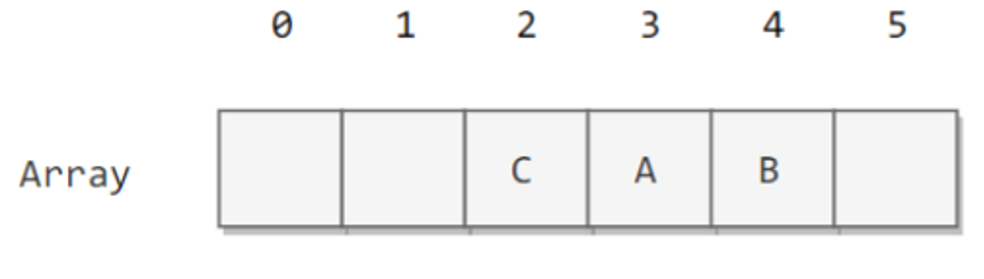
线性探测法的成本取决于连续条目的长度，连续条目也叫聚簇。当聚簇很长时，在查找和插入时也需要进行很多次探测。例如下图中 2~4 位置就是一个聚簇。

α = N/M，把 α 称为使用率。理论证明，当 α 小于 1/2 时探测的预计次数只在 1.5 到 2.5 之间。为了保证散列表的性能，应当调整数组的大小，使得 α 在 [1/4, 1/2] 之间。

private void resize() {if (N >= M / 2)resize(2 * M);else if (N <= M / 8)resize(M / 2);
}private void resize(int cap) {LinearProbingHashST<Key, Value> t = new LinearProbingHashST<Key, Value>(cap);for (int i = 0; i < M; i++)if (keys[i] != null)t.putInternal(keys[i], values[i]);keys = t.keys;values = t.values;M = t.M;
}

小结

1. 符号表算法比较

算法	插入	查找	是否有序
链表实现的无序符号表	N	N	yes
二分查找实现的有序符号表	N	logN	yes
二叉查找树	logN	logN	yes
2-3 查找树	logN	logN	yes
拉链法实现的散列表	N/M	N/M	no
线性探测法实现的散列表	1	1	no

应当优先考虑散列表，当需要有序性操作时使用红黑树。

2. Java 的符号表实现

• java.util.TreeMap：红黑树
• java.util.HashMap：拉链法的散列表

3. 稀疏向量乘法

当向量为稀疏向量时，可以使用符号表来存储向量中的非 0 索引和值，使得乘法运算只需要对那些非 0 元素进行即可。

public class SparseVector {private HashMap<Integer, Double> hashMap;public SparseVector(double[] vector) {hashMap = new HashMap<>();for (int i = 0; i < vector.length; i++)if (vector[i] != 0)hashMap.put(i, vector[i]);}public double get(int i) {return hashMap.getOrDefault(i, 0.0);}public double dot(SparseVector other) {double sum = 0;for (int i : hashMap.keySet())sum += this.get(i) * other.get(i);return sum;}
}

算法 - 符号表-上

😁热门专栏推荐
想学习vue的可以看看这个

java基础合集

数据库合集

redis合集

nginx合集

linux合集

手写机制

微服务组件

spring_尘觉

springMVC

mybits

等等等还有许多优秀的合集在主页等着大家的光顾感谢大家的支持

🤔欢迎大家加入我的社区 尘觉社区

文章到这里就结束了，如果有什么疑问的地方请指出，诸佬们一起来评论区一起讨论😁
希望能和诸佬们一起努力，今后我们一起观看感谢您的阅读🍻
如果帮助到您不妨3连支持一下，创造不易您们的支持是我的动力🤞