2331. 计算布尔二叉树的值

给你一棵 完整二叉树 的根，这棵树有以下特征：

• 叶子节点 要么值为 0 要么值为 1 ，其中 0 表示 False ，1 表示 True 。

• 非叶子节点 要么值为 2 要么值为 3 ，其中 2 表示逻辑或 OR ，3 表示逻辑与 AND 。

计算 一个节点的值方式如下：

• 如果节点是个叶子节点，那么节点的 值 为它本身，即 True 或者 False 。

• 否则，计算 两个孩子的节点值，然后将该节点的运算符对两个孩子值进行 运算 。

返回根节点 root 的布尔运算值。

完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。

叶子节点 是没有孩子的节点。

示例 1：

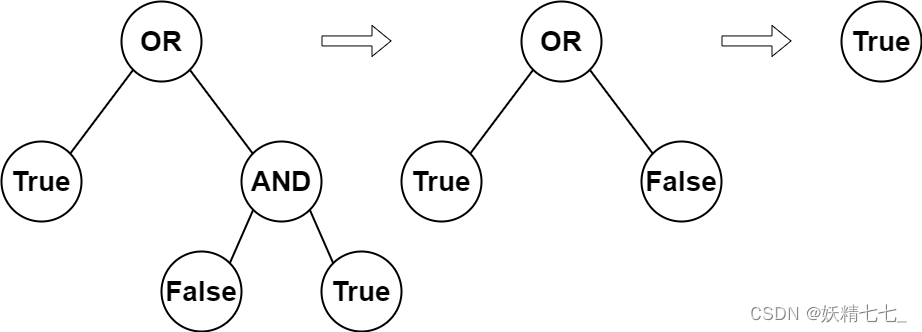
输入：root = [2,1,3,null,null,0,1] 输出：true 解释：上图展示了计算过程。 AND 与运算节点的值为 False AND True = False 。 OR 运算节点的值为 True OR False = True 。 根节点的值为 True ，所以我们返回 true 。

示例 2：

输入：root = [0] 输出：false 解释：根节点是叶子节点，且值为 false，所以我们返回 false 。

提示：

• 树中节点数目在 [1, 1000] 之间。

• 0 <= Node.val <= 3

• 每个节点的孩子数为 0 或 2 。

• 叶子节点的值为 0 或 1 。

• 非叶子节点的值为 2 或 3 。

定义递归函数，evaluateTree计算root这棵树的布尔值。

维护递归定义内部逻辑，先计算左右子树的布尔值，然后分类讨论。

bool rightbool = evaluateTree(root->right); if (root->val == 2) return leftbool || rightbool; else return leftbool && rightbool;

递归出口，如果root是叶子节点，直接返回自身即可，val==1返回true，否则返回false。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:bool evaluateTree(TreeNode* root) {// 定义递归函数evaluateTree，计算bool值// 递归的出口if (root->left == nullptr && root->right == nullptr)return root->val == 1 ? true : false;bool leftbool = evaluateTree(root->left);bool rightbool = evaluateTree(root->right);if (root->val == 2)return leftbool || rightbool;elsereturn leftbool && rightbool;}
};

时间复杂度分析：

假设每一个子问题都是同等规模。

T(N)=2*T(N/2)+O(1)。

a=2,b=2,d=0,a=b^k,k=1

T(N)=N。

空间复杂度分析：

递归函数evaluateTree的递归调用会使用系统栈空间来存储每一层递归的状态信息，因此空间复杂度取决于递归的深度。

在最坏情况下，空间复杂度取决于二叉树的高度，为O(h)；在平衡二叉树的情况下，空间复杂度为O(log n)。

此外，除了系统栈空间外，并没有使用额外的数据结构来存储节点信息，因此除了系统栈空间外，并不会额外消耗其他空间。

因此，该函数的时间复杂度为O(n)，空间复杂度为O(h)或O(log n)，取决于二叉树的形状。

129. 求根节点到叶节点数字之和

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

• 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3] 输出：25 解释： 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此，数字总和 = 12 + 13 = 25

示例 2：

输入：root = [4,9,0,5,1] 输出：1026 解释： 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此，数字总和 = 495 + 491 + 40 = 1026

提示：

• 树中节点的数目在范围 [1, 1000] 内

• 0 <= Node.val <= 9

• 树的深度不超过 10

定义dfs递归函数计算根节点到root树中的叶节点数字之和。

定义prevnums为根节点到root节点的数字。

维护递归函数定义内部逻辑，首先维护prevnums变量，如果root是叶子节点，此时prevnums变量存储的就是root根节点到叶子节点数字之和。返回prevnums即可。

如果root不是叶子节点，此时计算根节点到左树中的叶子节点数字和+根节点到右树中的叶子节点数字和。

递归出口，如果root只有一个节点，直接返回prevnums。

处理细节，如果root==nullptr，直接返回0。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:int sumNumbers(TreeNode* root) {// 定义dfs，计算root节点所构成的数字和，在prevnums的基础上。// 递归出口，叶子节点int prevnums = 0;return dfs(root, prevnums);}int dfs(TreeNode* root, int prevnums) {if(root==nullptr) return 0;prevnums = prevnums * 10 + root->val;if (root->left == nullptr && root->right == nullptr)return prevnums;int ret = 0;ret += dfs(root->left, prevnums);ret += dfs(root->right, prevnums);return ret;}
};

时间复杂度分析：

假设每一个子问题都是同等规模。

T(N)=2*T(N/2)+O(1)

a=2,b=2,d=0,a=b^k,k=1。

k>d,T(N)=O(N^K)=O(N)

空间复杂度分析：

递归函数sumNumbers的递归调用会使用系统栈空间来存储每一层递归的状态信息，因此空间复杂度取决于递归的深度。

在最坏情况下，空间复杂度取决于二叉树的高度，为O(h)，其中h为树的高度。

除了系统栈空间外，并没有使用额外的数据结构来存储节点信息，因此除了系统栈空间外，并不会额外消耗其他空间。

因此，该函数的时间复杂度为O(n)，空间复杂度取决于树的高度，为O(h)。

814. 二叉树剪枝

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

输入：root = [1,null,0,0,1] 输出：[1,null,0,null,1] 解释： 只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

输入：root = [1,0,1,0,0,0,1] 输出：[1,null,1,null,1]

示例 3：

输入：root = [1,1,0,1,1,0,1,0] 输出：[1,1,0,1,1,null,1]

提示：

• 树中节点的数目在范围 [1, 200] 内

• Node.val 为 0 或 1

定义递归函数pruneTree对root树进行剪枝的操作，返回剪枝之后的根节点。

维护递归函数内部逻辑，对左子树和右子树进行剪枝，此时链接左右子树。此时如果左右子树都是nullptr，并且root->val==0，此时直接返回nullptr。

递归出口，如果root==nullptr，不需要进行剪枝操作，直接返回nullpt。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {// 定义pruneTree对root进行剪枝，返回剪枝后的节点// 递归出口if (root == nullptr)return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if (root->val == 0 && root->left == nullptr && root->right == nullptr)return nullptr;return root;}
};

假设每一个子问题都是同等规模。

T(N)=2*T(N/2)+O(1)。

a=2,b=2,d=0,a=b^k,k=1。

k>d,T(N)=O(N^K)=O(N)。

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！