4.1 时间序列预测

设置现在有一个时间序列$s(k)$，对于观测者可以获得对应的观测值$x(k)$
$$x(k)=s(k)+n(k)+In(k)+J(k)$$
其中$n(k)$为测量误差/噪声，$In(k)$为自然干扰，$J(k)$为人为干扰。

现在我们已经构造好了一个观察的时间序列了。现在我们的目标是去时间序列预测，而我们可以利用是数据是历史滑动窗内的数据，这个滑动窗的大小为p。利用前p个观测值，来预测当前$s(k)$。

现在我们拥有N个时间序列的数据$x(1),x(2),...,x(N)$
设置前D个点$x(1),x(2),...,x(D)$用于训练，即训练集，其中D往往为N的75%~80%；
由此我们的测试集为$x(D+1),x(D+2),...,x(N)$

构造D-p个训练组
$$X^{(1)}=[x(1),...,x(p),x(p+1){]}^T,...,X^{(D-p)}=[x(D-p),...,x(D-1),x(D){]}^T,$$
其中每组的前p个数据作为训练FLS的输入，第p+1的数据作为FLS期望的输出。

同理有N-p-D个检测组
$$X^{(D+1)}=[x(D+1),...,x(D+p),x(D+p+1){]}^T,...,X^{(N-p)}=[x(N-p),...,x(N-1),x(N){]}^T,$$

值得注意的是，这里的每个训练组都可以为FLS预测器训练对应的规则，而测试集则用于测试各被提取的规则的精度性能。

4.2 提取规则的方法

4.2.1 One-pass method（一次性方法）

4.2.1.1数据赋值法

该方法是利用数据来构造出在规则的前因（antecedent）和后因（consequent）中的模糊集的中心

例子1

如果现在$F_i^l$是一个为Gaussian MF的模糊集
μ F i l ( x i ) = exp ⁡ { − ( x i − m F i l ) 2 2 σ F i l 2 } , i = 1 , 2 , . . . , p \mu_{F_i^l}(x_i)=\exp \{-\frac{(x_i-m_{F_i^l})^2}{2\sigma_{F_i^l}^2}\},i=1,2,...,p μFil​​(xi​)=exp{−2σFil​2​(xi​−mFil​​)2​},i=1,2,...,p
对于一个规则来说，前因参数数目为2p，后因参数数目为1，
现在我们有D-p个测试组，即有D-p个规则，那么总共涉及到了$(2p+1)(D-p)$个参数。

针对以上的例子，问题的关键是，我们应该如何去选择大量的MF和初始化大量的参数

4.2.1.1 WM方法

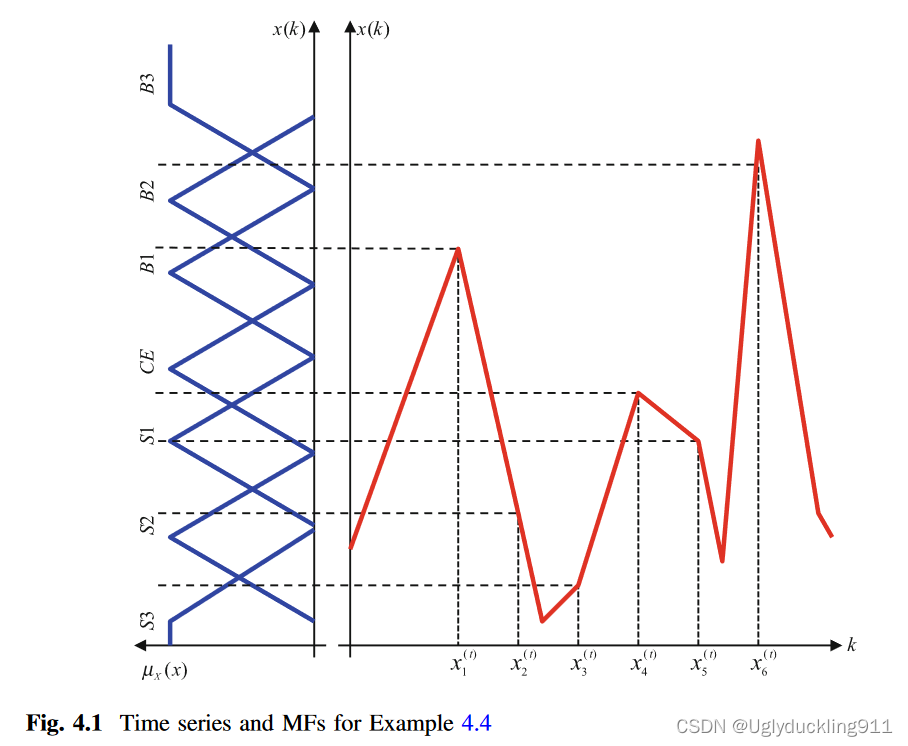该方法主要是通过预指定好前因和后因的数据，然后将将这些数据关联起来
以上图为例，

• 首先，设计好关于$x^{(l)}$的自由度${\mu }_x(x)$；
• 然后将时间序列映射到其中最大的自由度对应的值；
• 由此得到一个具有输入输出关系的规则了

以上图为例，$x_1\to B_1,x_2\to S_2,x_3\to B_3,x_4\to CE,...$

但是以上的WM方法也存在一个问题就是，对于大量的数据，可能产生相互矛盾的规则。
对于这样的现象，我们往往选择从中选择一个最大值的情况。

以上介绍了数据赋值方法和WM方法都属于One-pass方法，特点都是比较简单，可实现；但需要大量的参数和规则提前设定

接下来，我们的目标是构造一个FLS框架，利用数据来最优化参数并减少规则。

4.2.2 最小二乘法

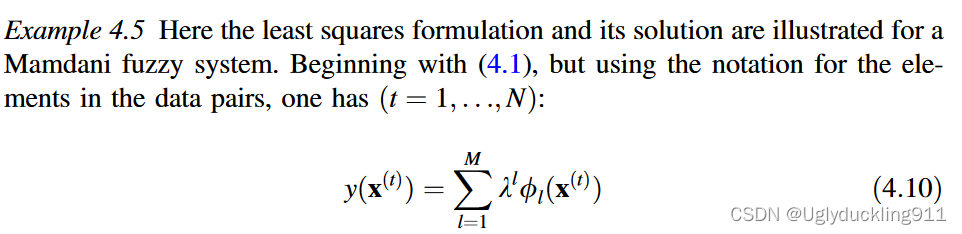
4.2.3 基于导数的方法

两种最流行和广泛使用的基于导数的优化算法是 steepest 下降和 Marquardt-Levenberg。使用它们时，不会提前固定任何前因或后因参数。这两种算法都需要关于每个 MF 参数的数学目标函数的一阶导数。在本节中，重点介绍单例 Mamdani 模糊系统和乘积 t 范数的最陡峭下降算法

最速下降优化算法仅对每个 $e^{(t)}$更新一次参数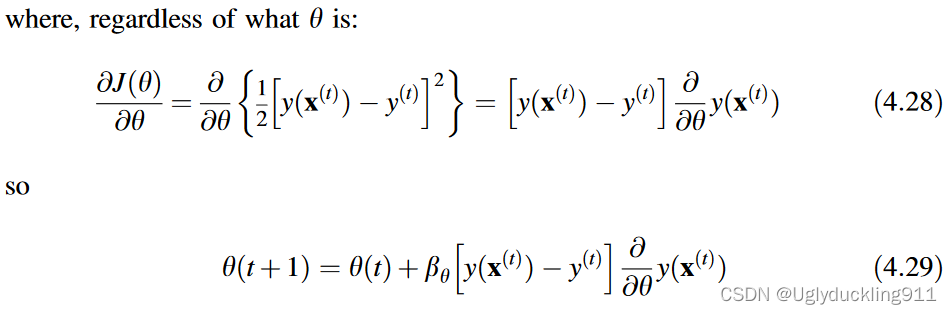$\theta$

• 如果 MF 在其域上更改其数学公式（例如，三角形和梯形 MF 的情况），则导数公式也会更改，并且必须包括耗时的域测试。
• 他们倾向于只找到目标函数的局部极值而不是全局极值，也就是说，他们倾向于被困在局部极值。当然，有一些方法可以避免被困住，但是当使用衍生品时，有被困的倾向。
• 如何选择FBF的数量，M，是一个悬而未决的问题。下一个方法可用于解决此缺点。

4.2.4 SVD-QR方法

对于模糊系统来说，规则分解可能是一个问题，而奇异值分解 （SVD） 是规则约简的一种方法。矩阵的 SVD 是数值线性代数中非常强大的工具。它的重要用途包括确定矩阵的秩和线性最小二乘问题的数值解。它可以应用于正方形或矩形矩阵，其元素要么是实数，要么是复数

4.2.6 迭代法