一、 实验目的
1.加深学生对算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;
2.提高学生利用课堂所学知识解决实际问题的能力;
3.提高学生综合应用所学知识解决实际问题的能力。
二、实验任务
1、【ACM、面试题】求解按“最多排序”到“最小排序”的顺序排列问题。一个序列中的“未排序”的度量是相对于彼此顺序不一致的条目对的数量,例如,在字母序列“DAABEC”中,该度量为5,因为D大于右边是4个字母,E大于其右边的1个字母。该度量称为该序列的逆序数。序列“AACEDGG”只有一个逆序对(E和D),它几乎被排序好了,而序列“ZWQM”有6个逆序对,它是未排序的,恰好是反序。
你需要对若干个DNA序列(仅包含4个字母A、C、G和T的字符串)分类,注意是分类而不是按字母顺序排序,而是按照“最多排序”到“最小排序”的顺序排列,所有DNA序列的长度都相同。
输入:第一行包含两个整数:n(0<n≤50)表示字符串长度,m(0<m≤100)表示字符串个数。后面是m行,每行包含一个长度为n的字符串。
输出:按“最多排序”到“最小排序”的顺序输出所有字符串。若两个字符串的逆序对个数相同,按原始顺序输出它们。
2、字符串匹配算法(BF,KMP)
给定一个文本,在该文本中查找并定位任意给定字符串。
3、循环赛日程安排问题
设有n=2k个选手要进行网球循环赛,要求设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能赛一次。
4、采用分治法求解最大连续子序列和问题
给定一个有n(n≥1)个整数的序列,要求求出其中最大连续子序列的和。
例如:
序列(-2,11,-4,13,-5,-2)的最大子序列和为20
序列(-6,2,4,-7,5,3,2,-1,6,-9,10,-2)的最大子序列和为16。
规定一个序列最大连续子序列和至少是0(长度为0的子序列),如果小于0,其结果为0。
5、 采用动态规划法求解最大连续子序列和问题
三、实验设备及编程开发工具
实验设备:Win10 电脑
开发工具:Visual Studio 2019
编程语言:C/JAVA
四、实验过程设计(算法设计过程)
(一)、DNA序列分类
1、算法分析:
输入字符的时候可以利用string对象来处理。在计算逆序对时要按照逆序对从小到大的顺序输出,这里有个小技巧,多定义一个数组来存放原始顺序的逆序对数,然后对求取到的逆序对进行从小到大的排序,最后将备用存放逆序对的数组数据跟排好序的进行比较,然后对应原始下标输出对应的字符串即可。
2、代码实现:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;int n, m;
string a[55];
int t[110]={0},r[110];int s(string a)
{int sum = 0;for(int i = 0; i < a.length()-1; i++)for(int j = i+1; j < a.length(); ++j)if(a[i] > a[j])sum++;return sum;
}int main()
{int x = 0;cout << "请输入字符串长度和字符串个数:\n"; scanf("%d%d",&n,&m);cout << "请输入所有的字符串:\n";for (int i = 0; i < m; ++i){cin >> a[i];}for(int i = 0; i < m; i++){ t[i] = s(a[i]);r[i] = t[i];}sort(t,t+m);cout << "=================\n";cout << "排序后的字符串顺序为:\n";for(int i = 0; i < m; i++)for(int j = 0; j < m; j ++){if(t[i] == r[j])cout << a[j] << endl;}return 0;}DNA序列分类
1、实验结果
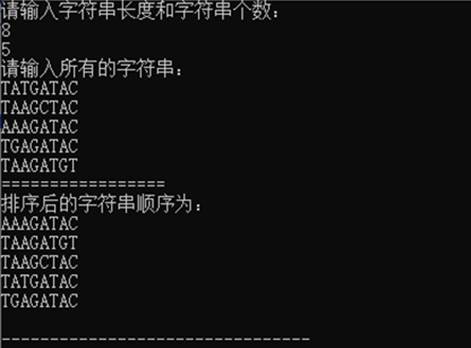
2、算法复杂度分析
时间复杂度:O(n^2)
二)、字符串匹配
1、算法分析:
首先,原字符串和子串左端对齐,比较第一个字符,发现不相等,子串向后移动,直到子串的第一个字符能和原字符串匹配。 当A匹配上之后,接着匹配后续的字符,直至原字符串和子串出现不相等的字符为止。参见kmp算法。
2、代码实现:
#include "vector"
#include "string"
#include <iostream>
#include "algorithm"using namespace std;//计算模式P的部分匹配值,保存在next数组中
void MakeNext(const string &P, vector<int> &next)
{int q,k;//k记录所有前缀的对称值 int m = P.size();//模式字符串的长度 next[0] = 0;//首字符的对称值肯定为0 for (q = 1, k = 0; q < m; ++q)//计算每一个位置的对称值 {//k总是用来记录上一个前缀的最大对称值 while (k > 0 && P[q] != P[k])k = next[k - 1];//k将循环递减,值得注意的是next[k]<k总是成立 if (P[q] == P[k])k++;//增加k的唯一方法 next[q] = k;//获取最终值 }
}void KmpMatch(const string &T, const string &P, vector<int> &next)
{int n, m;n = T.size();m = P.size();MakeNext(P, next);for (int i = 0, q = 0; i < n; ++i){while (q > 0 && P[q] != T[i])q = next[q - 1];if (P[q] == T[i])q++;if (q == m){cout << "模式文本的偏移为:" << (i - m + 1) << endl;q = next[q - 1];//寻找下一个匹配}}
}int main()
{system("color 0A");vector<int> next(20,0);//保存待搜索字符串的部分匹配表(所有前缀函数的对称值)string T = "abcdefgikjhgdjahfsdhgfusgr";//文本string P = "sdhg";//待搜索字符串cout <<"文本字符串:"<< T << endl;cout <<"模式字符串:"<< P << endl;KmpMatch(T, P, next);return 0;
}字符串匹配
1、实验结果
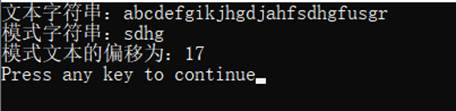
2、算法复杂度分析
时间复杂度:O(m+n)
(三)、循环赛日程安排
1、算法分析:
按照要求,可以将比赛表设计成一个n行n-1列的二维表,其中第i行第j列的元素表示和第i个选手在第j天比赛的选手号。采用分治策略,可将所有参加比赛的选手分成两部分, n = 2 k n=2^k n=2k个选手的比赛日程表就可以通过 n = 2 ( k − 1 ) n=2^{(k-1)} n=2(k−1)个选手的的比赛日程表来决定。递归的执行这样的分割,直到只剩下两个选手,比赛日程表的就可以通过这样的分治策略逐步构建。
假设有 2 1 2^1 21个选手,其安排如下:
| 1 | 2 |
|---|---|
| 2 | 1 |
假设有 2 2 2^2 22个选手,其安排如下:
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 2 | 1 | 4 | 3 |
| 3 | 4 | 1 | 2 |
| 4 | 3 | 2 | 1 |
假设有 2 3 2^3 23个选手,其安排如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 4 | 4 | 6 | 5 | 8 | 7 |
| 3 | 4 | 1 | 2 | 7 | 8 | 5 | 6 |
| 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 |
| 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| 6 | 5 | 8 | 7 | 2 | 1 | 4 | 3 |
| 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2 |
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
根据以上的规律,求解过程可以看作四个部分:
-
求左上角子表:左上角子表是前 2 ( k − 1 ) 2^{(k-1)} 2(k−1)个选手的比赛前半程的比赛日程。
-
求左下角子表:左下角子表是剩余的 2 ( k − 1 ) 2^{(k-1)} 2(k−1)个选手的比赛前半程比赛日程。这个子表和左上角子表的对应关系式,对应元素等于左上角子表对应元素加 2 ( k − 1 ) 2^{(k-1)} 2(k−1)。
-
求右上角子表:等于左下角子表的对应元素。
-
求右下角子表:等于左上角子表的对应元素。
2、代码实现:
#include<stdio.h>
#include<math.h>
#define N 50
void GameTable(int k,int array[][N]);
void print(int k,int array[][N]); //输出二维数组
main()
{int k;int array[N][N];printf("参赛选手的人数为n(n=2^k),请输入k 的值:");do{scanf("%d",&k);if(k>0){GameTable(k,array);print(k,array);}elseprintf("您输入的数据有误,请重新输入"); }while(k!=0);//排除输入错误k值}
void GameTable(int k,int array[][N])//数组下标从1开始
{int i,j,s,t;int n=1;for(i=1;i<=k;i++)n*=2; //求总人数for(i=1;i<=n;i++)array[1][i]=i; //第一行排1-8int m=1; //用来控制每一次填表时i行j列的起始填充位置for(s=1;s<=k;s++) //s指对称赋值的总循环次数,即分成几大步进行制作日程表{n=n/2;for(t=1;t<=n;t++) //t指明内部对称赋值的循环次数for(i=m+1;i<=2*m;i++)for(j=m+1;j<=2*m;j++){array[i][j+(t-1)*m*2]=array[i-m][j+(t-1)*m*2-m]; //右上角等于左上角的值array[i][j+(t-1)*m*2-m]=array[i-m][j+(t-1)*m*2]; //左下角等于右上角的值}m*=2;}}
void print(int k,int array[][N])
{int i,j;int num=pow(2,k);printf("%d人的循环赛日程表如下:\n",num);for(i=1;i<=num;i++) //输出二维数组 {for(j=1;j<=num;j++){printf("%d\t",array[i][j]);}printf("\n");}
}循坏日程赛安排
1、实验结果
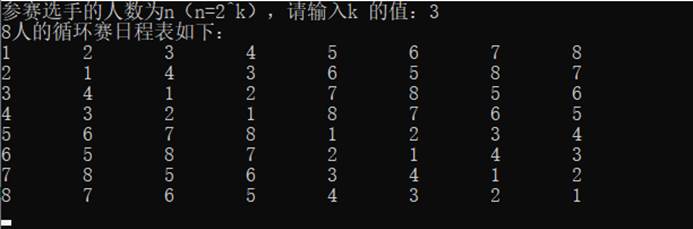
2、算法复杂度分析
时间复杂度:O(2^k * 2^k)。
(四)、(分治)最大连续子序列和
1、算法分析:
1.将一个长度为n的序列,一分为二变为两个长度为n/2的子序列,继续将子序列们一分为二,直到每个子序列只含有1个整数。
2.此时问题已经足够小,“最大子序列和”有以下三种情况:左边序列的最大子序列和、右边序列的最大子序列和和处在中间位置上的最大子序列和,我们通过比较,得到三者中的最大值。
3.再将这些“小问题”合并,使用同样的比较方法逐步向上合并这些“左右序列”,直到得到整个序列的最大子序列和,解决问题。
2、代码实现:
#include<stdio.h>
#define MAXSIZE 100int max3(int a,int b,int c)
{if(a>b) return a>c?a:c;else return b>c?b:c;
}int MaxSubseqSum(int a[],int left,int right)
{int maxLeftSum,maxRightSum,maxMidSum;int maxLeftBorderSum,LeftBorderSum;int maxRightBorderSum,RightBorderSum;int mid;int i;if(left==right) //递归出口,子序列只有一个元素时return a[left];mid=(left+right)/2; //求中间位置maxLeftSum=MaxSubseqSum(a,left,mid); //求左边序列的最大子序列和maxRightSum=MaxSubseqSum(a,mid+1,right); //求右边序列的最大子序列和maxLeftBorderSum=0;LeftBorderSum=0;for(i=mid;i>=left;i--) //从中间位置向左找靠边界的最大子序列{LeftBorderSum+=a[i];if(LeftBorderSum>maxLeftBorderSum)maxLeftBorderSum=LeftBorderSum;}maxRightBorderSum=0;RightBorderSum=0;for(i=mid+1;i<=right;i++) //从中间位置向右找靠边界的最大子序列{RightBorderSum+=a[i];if(RightBorderSum>maxRightBorderSum)maxRightBorderSum=RightBorderSum;}maxMidSum=maxLeftBorderSum+maxRightBorderSum; //得到处在中间位置上的最大子序列和return max3(maxLeftSum,maxRightSum,maxMidSum);
}int MaxNum(int a[],int left,int right)
{int maxLeft,maxRight;int mid;if(left==right)return a[left];mid=(left+right)/2;maxLeft=MaxNum(a,left,mid);maxRight=MaxNum(a,mid+1,right);return maxLeft>maxRight?maxLeft:maxRight;
}int main()
{int a[MAXSIZE];int count=0;int i,n;printf("序列长度:");scanf("%d",&n);printf("输入整数序列:");for(i=0;i<n;i++){scanf("%d",&a[i]);if(a[i]<=0)count++;}if(count==n) //判断是否含有正整数printf("最大子序列和:%d\n",MaxNum(a,0,n-1));elseprintf("最大子序列和:%d\n",MaxSubseqSum(a,0,n-1));}(分治)最大连续子序列和
1、实验结果
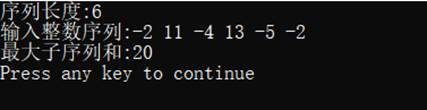
2、算法复杂度分析
时间复杂度:O(nlog(n))
(五)、(动态规划)最大连续子序列和
1、算法分析:
- 动态规划算法:求最大连续子序列
1) k[j] 表示最大连续子序列最后一个元素,dk[j]表示最大连续子序列和
2)最大连续子序列和为从 dk[i] ~ dk[j] - 分两种情况:
1)最大和为k[j]。它之前的序列和都小于k[j]
2)最大和为dk[j-1]+k[j]。
3.得到状态转移方程:
dk[j] = max{dk[j-1]+k[j], k[j]} 边界为 dk[0] = j[0] - 动态规划算法计算特点(步骤):
从后往前算,每步计算结果都记录进表。
计算结束后,再遍历记录表。
2、代码实现:
import java.util.Scanner;public class MaxSubSequence {public static void main(String[] args) {Scanner sc = new Scanner(System.in);System.out.println("请输入子序列长度:");int N = sc.nextInt();System.out.println("请输入子序列:");int[] A = new int[N];for (int i = 0; i < A.length; i++) {A[i] = sc.nextInt();}int ThisSum, MaxSum, j;ThisSum = MaxSum = 0;for (j = 0; j < N; j++) {ThisSum += A[j];if (ThisSum > MaxSum)MaxSum = ThisSum;else if (ThisSum < 0)ThisSum = 0;}System.out.println("最大子序列和位:" + MaxSum);}
}(动态规划)最大连续子序列和
1、实验结果
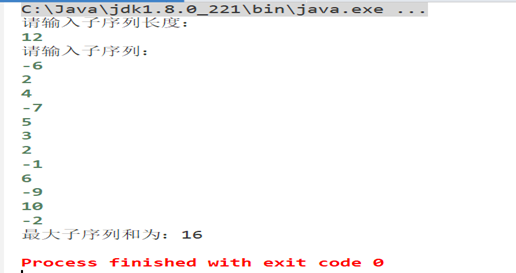
2、算法复杂度分析
时间复杂度:0(n)
五、实验小结(包括问题和解决方法、心得体会等)
分治法,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。本次实验增加了动手编码能力,对算法设计有了更进一步的认识,但是技术上的缺陷,编码能力上存在的短板,在今后的实验中还需要加大练习力度。