在过去一周里,比特币价格经历了一段下跌,并在随后出现了一些反弹迹象。与此同时,链上数据显示,巨鲸们在囤积稳定币,预示着“强烈的看涨情绪”。以太坊方面,美国证券交易委员会(SEC)已开放对三项以太币现货ETF提案发表评论的窗口,但现下行业分析师对其能否顺利通关变得不那么乐观。

数据显示,比特币价格最近出现了复苏迹象,多头在近期下跌后纠正走势的"高效率",给市场观察人士留下了深刻的印象,交易员和分析师指出,这些反弹主要来自现货市场的买盘,而不是衍生品市场。虽然这种势头需要持续一段时间才能实现持久的变化,但随着价格上涨,那些做空比特币的人可能会面临问题。
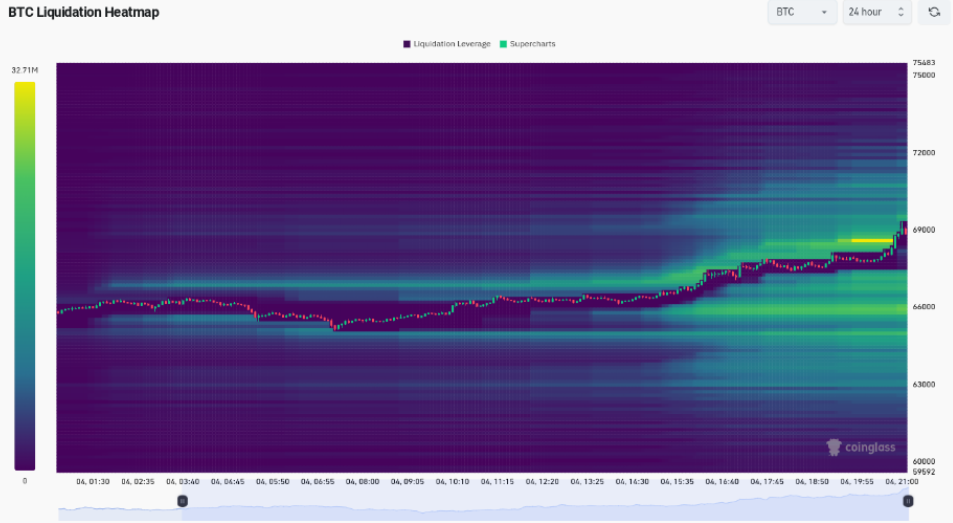
监控资源显示,随着比特币突破68620美元,一堵价值3270万美元的流动性墙被拆除。然而,69000美元仍然是一个重要的阻力位,这是自2021年底以来比特币价格的历史高点,也是关键的价格焦点。
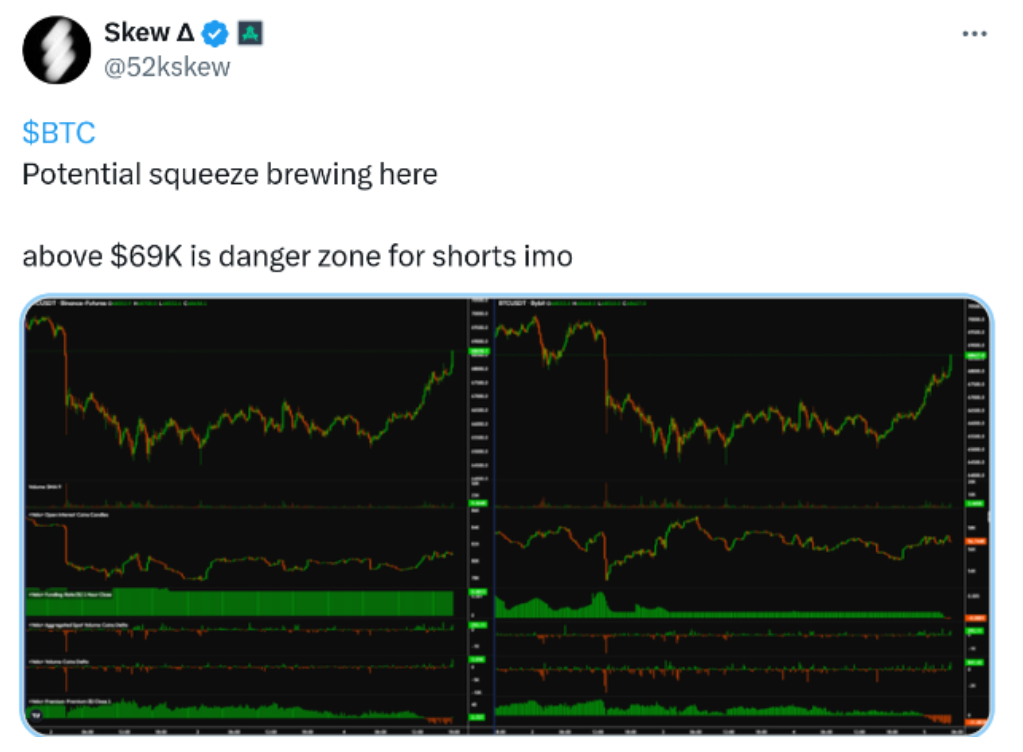
除了交易所币安的BTC/USDT订单簿数据图表外,另一位交易员也将69000美元描述为一个重要的关键位。他解释说,对于了解市场对更高价格的实际需求来说,从这个水平开始的下跌非常重要。
著名交易员兼分析师Josh Rager表示,200周期指数移动平均线在4小时时间范围内为比特币提供了有效支撑,比特币还有上涨的空间,收盘价可能会超过71000美元。
与此同时,链上数据显示,巨鲸们在囤积稳定币。这些巨鲸背后所代表的往往是传统金融资金,预示着“强烈的看涨情绪”。而新增的稳定币要么是大资金在布局进场准备抄底,要么是巨鲸们提前抛售比特币的结果,引起了市场的广泛关注,因为巨鲸的举动通常被视为市场趋势的指示。
以太坊方面,市场最关注的莫过于SEC是否会在5月前通过以太坊现货ETF。目前已经有9个以太坊现货ETF的申请,其中最早面临最终审批期限的是VanEck,SEC需要在5月23日前决定是否批准他们的申请。
SEC目前还没有积极与各家发行商进行协商,这使得市场对于在五月获批的预期降低。然而,最近的情况似乎有所转机。根据4月2日发布的通知,SEC正在公开征求对于Bitwise、Fidelity和Grayscale提出的关于允许以太坊现货ETF在各大交易所上市和交易的规则改动提案的意见。
公众在这些提案发布在联邦公报(Federal Register)后有21天的时间提出回应。Bitwise和Grayscale提出在纽约证券交易所Arca上市交易,而Fidelity选择了Cboe BZX交易所。有一些人认为这是SEC积极推进以太坊现货ETF的信号,增加了其在五月获批的可能性。

然而,彭博ETF分析师James Seyffart表示,从19b-4表格来看,征求公众意见是标准程序,每个19b-4的ETF申请都要经历相同的流程,无论最终是批准还是拒绝。对于以太坊ETF来说,并没有构成任何形式的利好消息。
实际上,SEC在3月8日已经征求公众意见,针对以太坊ETF申请中潜在的批准问题。其中,SEC询问了以太坊转向权益证明(PoS)机制是否存在欺诈和操纵风险,需要关注这一问题。
对此,Metamask钱包开发商Consensys于3月29日提交了评论信,回应了这种担忧,并表示以太坊的PoS机制在安全性方面甚至超过了比特币的PoW机制。他们指出,基于比特币的ETF已经获得了SEC的批准上市交易,因此也主张以太坊现货ETF应该获得批准。

总结
总之,比特币和以太坊在最近一周都经历了波动。比特币价格出现了一些反弹迹象,并且多头市场在现货市场上表现出较强的买盘。然而,市场对比特币价格在69000美元附近的阻力位持谨慎态度。美SEC呼吁公众对以太币ETF提供意见,但并没有构成任何形式的利好消息。
因此,市场对于比特币和以太坊的未来走势仍存在不确定性。各种因素,包括市场情绪、监管决策和投资者行为,都可能对加密货币市场产生影响。因此,投资者应该保持谨慎,并在进行任何投资之前进行充分的研究和尽职调查。
![[HackMyVM]靶场Birthday](https://img-blog.csdnimg.cn/direct/935aef11ee634a6681b652c6b3d06fe6.png)