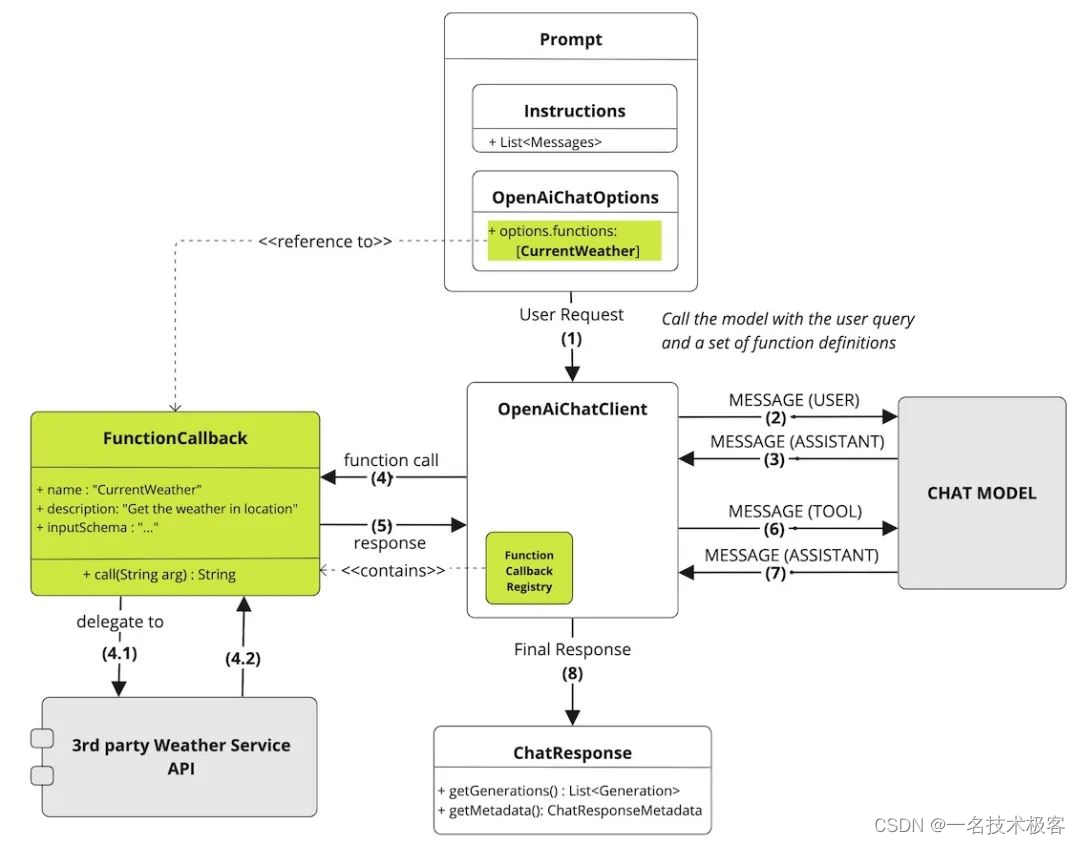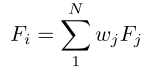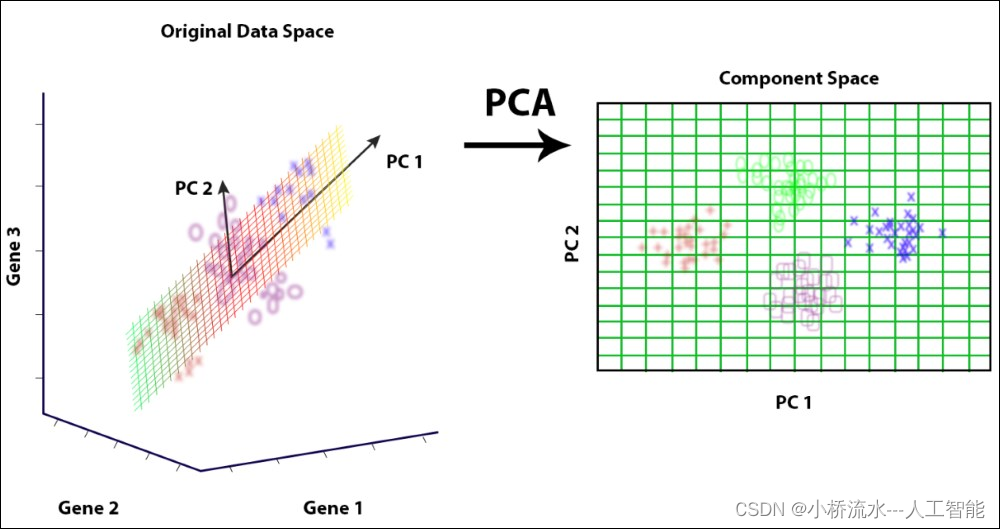
PCA(Principal Component Analysis,主成分分析)是一种广泛应用于数据分析和机器学习的技术,主要用于数据降维和特征提取。在PCA中,协方差矩阵起着核心作用,它描述了数据集中不同特征(变量)之间的线性相关性。
协方差矩阵的每一个元素表示了数据集中两个不同特征之间的协方差,即它们共同变化的程度。协方差是一个衡量两个随机变量之间线性关系的统计量。具体来说,协方差可以反映两个变量是如何一起变化的:如果它们同时增大或减小,协方差为正;如果一个增大而另一个减小,协方差为负;如果它们之间没有明确的线性关系,协方差可能接近于零。
然而,协方差和协方差矩阵只能衡量变量之间的线性关系,这是由它们的定义和计算方法所决定的。对于非线性关系,协方差无法提供有效的度量。这是因为协方差的计算基于的是两个变量之间的差的乘积的平均值,这种计算方式只能捕捉线性变化模式,而无法捕捉更复杂的非线性模式。
在PCA中,我们假设数据中的主要变化可以由其特征的线性组合来表示。因此,PCA通过计算协方差矩阵来找到数据中的最大方差方向,即主成分,这些主成分能够最好地表示数据的线性结构。但是,如果数据中存在非线性关系,PCA可能无法有效地提取这些关系,因为协方差矩阵无法描述这些非线性模式。
为了处理非线性关系,可能需要使用其他更复杂的方法,如核主成分分析(Kernel PCA)或其他非线性降维技术。这些方法通过引入非线性变换或核函数来扩展PCA的能力,使其能够捕捉和处理数据中的非线性结构。
综上所述,PCA中的协方差矩阵只能衡量变量之间的线性相关性,而不能衡量非线性关系,这是由协方差的定义和PCA的基本假设所决定的。在处理包含非线性关系的数据时,可能需要考虑使用其他更适合的方法。
总结
PCA(Principal Component Analysis)中的协方差矩阵只能衡量变量之间的线性相关性,而不能衡量非线性关系,主要原因如下:
-
线性假设:PCA假设数据是线性相关的,即特征之间的关系可以通过线性组合来表示。因此,PCA中使用协方差矩阵来衡量特征之间的相关性,它基于特征之间的线性关系进行计算。
-
协方差的局限性:协方差是衡量两个变量之间线性关系的统计量,它只能反映变量之间的线性相关性,无法捕捉非线性关系。在存在非线性关系的情况下,协方差矩阵的结果可能会失真,导致主成分无法有效地提取数据的特征。
-
主成分的线性组合:PCA通过寻找使得数据变换后方差最大的线性组合来构建主成分,这意味着PCA提取的主成分是原始特征的线性组合,无法捕捉非线性关系。
因此,虽然PCA是一种强大的降维技术,但它适用于线性相关的数据集。对于包含非线性关系的数据集,PCA可能无法提供准确的降维结果。在处理非线性数据时,通常需要使用其他方法,如核PCA等,来捕捉数据中的非线性结构。