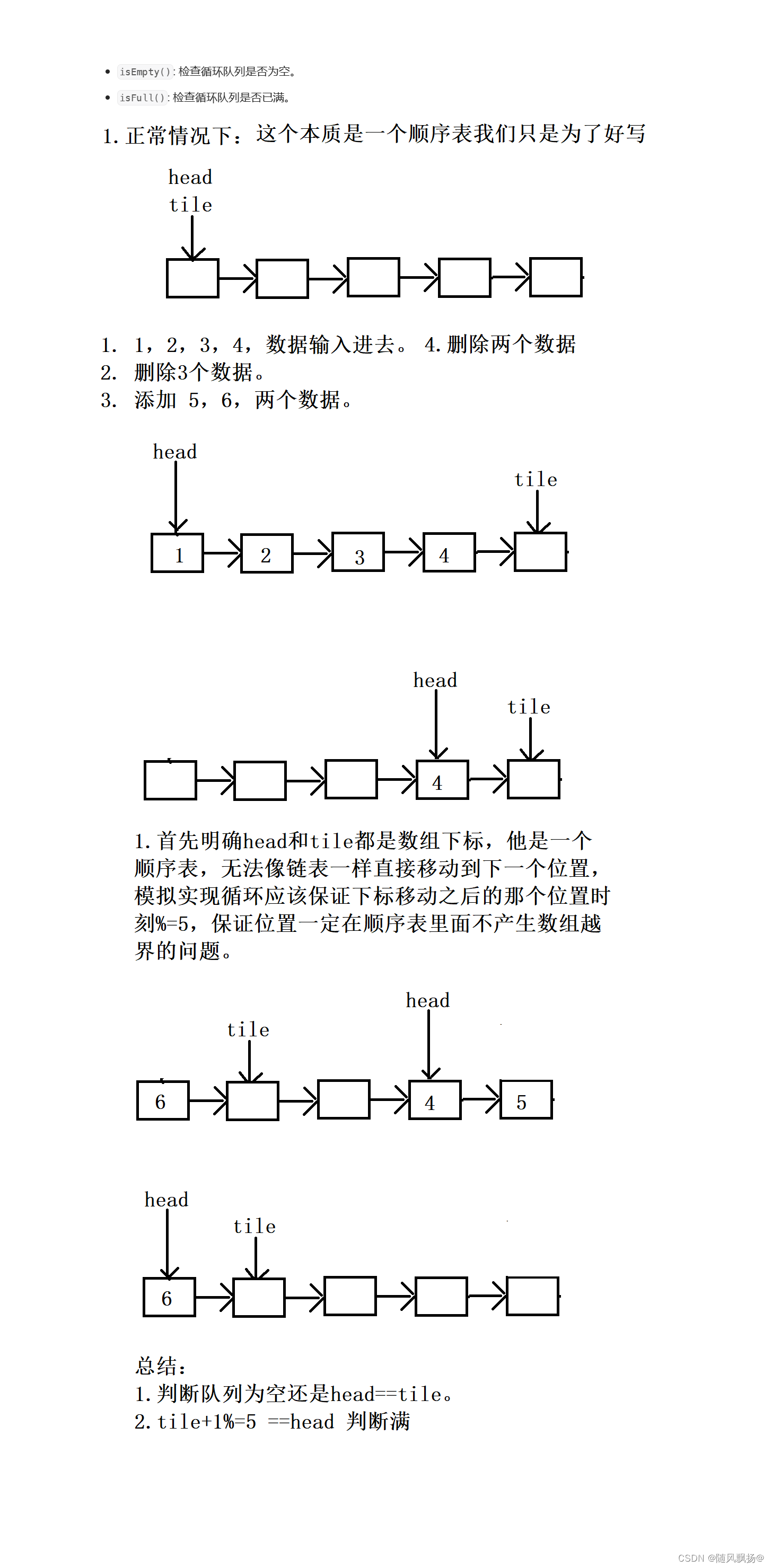
文章目录
- 写在前面
- 哈夫曼树及哈夫曼编码的算法实现
- 实验内容
- 代码实现
- 图的基本操作
- 实验内容
- 代码实现
写在前面
本篇实验代码非本人写,代码源自外部,经调试解决了部分warning和error后在本地vs上可以正常运行,如有运行失败可换至vs
未来会重构实现该两个实验
哈夫曼树及哈夫曼编码的算法实现
实验内容
内容要求:
1、初始化(Init):能够对输入的任意长度的字符串s进行统计,统计每个字符的频度,并建立哈夫曼树
2、建立编码表(CreateTable):利用已经建好的哈夫曼树进行编码,并将每个字符的编码输出。
3、编码(Encoding):根据编码表对输入的字符串进行编码,并将编码后的字符串输出。
4、译码(Decoding):利用已经建好的哈夫曼树对编码后的字符串进行译码,并输出译码结果。
测试数据:
输入字符串“thisprogramismyfavourite”,完成这28个字符的编码和译码。
代码实现
#include<iostream>
#include<string.h>
#include<queue>
#define MAX 10000
using namespace std;
char a[100], buff[1024], p;
typedef struct
{char letter, * code;int weight;int parent, lchild, rchild;
}HTNode, * HuffmanTree;int n;
char coding[100];int Min(HuffmanTree& HT, int i)
{int j;int k = MAX;int flag=0;for (j = 0; j <= i; ++j){if (HT[j].weight < k && HT[j].parent == 0){k = HT[j].weight;flag = j;}}HT[flag].parent = 1;return flag;
}void Select(HuffmanTree& HT, int i, int& s1, int& s2)
{s1 = Min(HT, i);s2 = Min(HT, i);
}void CreateHuffmanTree(HuffmanTree& HT, char t[], int w[])
{int m;int i, s1, s2;if (n <= 1)return;m = 2 * n - 1; HT = new HTNode[m + 1];for (i = 0; i < n; i++){char arr[] = "0";char* pa = arr;HT[i].code = pa;HT[i].parent = 0;HT[i].lchild = -1;HT[i].rchild = -1;HT[i].letter = t[i];HT[i].weight = w[i];}for (i = n; i <= m; i++){char arr[] = "0";char* pa = arr;HT[i].code = pa;HT[i].parent = 0;HT[i].lchild = -1;HT[i].rchild = -1;HT[i].letter = ' ';HT[i].weight = 0;}cout << "********************************" << endl;for (i = n; i < m; i++){Select(HT, i - 1, s1, s2);HT[s1].parent = i;HT[s2].parent = i;HT[i].lchild = s1;HT[i].rchild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}void CreatHuffmanCode(HuffmanTree HT)
{int start, c, f;int i;char* cd = new char[n];cd[n - 1] = '\0';cout << "字符编码为:" << endl;for (i = 0; i < n; i++){start = n - 1;c = i;f = HT[i].parent;while (f != 0) {--start;if (HT[f].lchild == c) {cd[start] = '0';}else {cd[start] = '1';}c = f;f = HT[f].parent;}HT[i].code = new char[n - start];strcpy(HT[i].code, &cd[start]);cout << HT[i].letter << ":" << HT[i].code << endl;}delete[] cd;
}void HuffmanTreeDecode(HuffmanTree HT, char cod[], int b)
{char sen[100];char temp[50];char voidstr[] = " ";int t = 0;int s = 0;int count = 0;for (int i = 0; i < b; i++){temp[t++] = cod[i];temp[t] = '\0';for (int j = 0; j < n; j++) {if (!strcmp(HT[j].code, temp)) {sen[s] = HT[j].letter;s++;count += t;strcpy(temp, voidstr);t = 0;break;}}}if (t == 0) {sen[s] = '\0';cout << "译码为:" << endl;cout << sen << endl;}else {cout << "二进制源码有错!从第" << count + 1 << "位开始" << endl;}
}int main()
{HuffmanTree HT;int b[100]={0};int i, j;int symbol = 1, x, k;cout << "请输入一段文字:";cin >> buff;int len = (int)strlen(buff);for (i = 0; i < len; i++){for (j = 0; j < n; j++){if (a[j] == buff[i]){b[j] = b[j] + 1;break;}}if (j >= n){a[n] = buff[i];b[n] = 1;n++;}}cout << "字符和权值信息如下" << endl;for (i = 0; i < n; i++){cout << "字符:" << a[i] << " 权值:" << b[i] << endl;}CreateHuffmanTree(HT, a, b);CreatHuffmanCode(HT);cout << "文字编码为:\n";for (int i = 0; i < len; i++){for (int j = 0; j < n; j++){if (buff[i] == HT[j].letter){cout << HT[j].code;break;}}}cout << "\n译码:" << endl;while (1){cout << "请输入要译码的二进制字符串,输入'#'结束:";x = 1;k = 0; symbol = 1;while (symbol) {cin >> p;if (p != '1' && p != '0' && p != '#') {x = 0;}coding[k] = p;if (p == '#')symbol = 0;k++;}if (x == 1) {HuffmanTreeDecode(HT, coding, k - 1);}else {cout << "有非法字符!" << endl;}cout << "是否继续?(Y/N):";cin >> p;if (p == 'y' || p == 'Y')continue;elsebreak;}return 0;
}
图的基本操作
实验内容
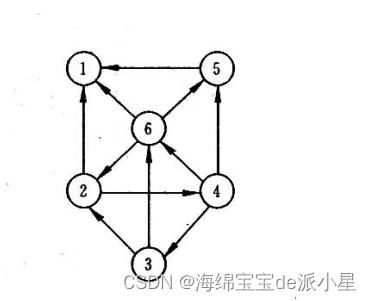
分别用邻接矩阵和邻接表对如下有向图实现:
1.输出存储结果;
2.计算各结点的出度和入度,并输出;
3.实现图的深度优先遍历和广度优先遍历,并输出。
代码实现
#include<stdio.h>
#include<stdlib.h>#define MAXVEX 50
int visit[MAXVEX];
int in_deg[MAXVEX];//入度
int out_deg[MAXVEX];//出度 typedef struct
{int vertices[MAXVEX];int arc[MAXVEX][MAXVEX];int vexnum, arcnum;
}MGraph;typedef struct queue
{int* pBase;int front, rear;
}QUEUE;void init_queue(QUEUE* Q)
{Q->pBase = (int*)malloc((sizeof(int)) * MAXVEX);Q->front = 0;Q->rear = 0;
}bool isfull_queue(QUEUE* Q)
{if (((Q->rear + 1) % MAXVEX) == Q->front)return true;elsereturn false;
}bool isempty_queue(QUEUE* Q)
{if (Q->rear == Q->front)return true;elsereturn false;
}void in_queue(QUEUE* Q, int val)
{if (isfull_queue(Q))return;Q->pBase[Q->rear] = val;Q->rear = (Q->rear + 1) % MAXVEX;
}int out_queue(QUEUE* Q)
{int temp = 0;if (isempty_queue(Q))return 0;temp = Q->pBase[Q->front];Q->front = (Q->front + 1) % MAXVEX;return temp;
}void BFS(MGraph G, QUEUE* Q, int v)
{if (!visit[v]) {visit[v] = 1;printf("%d ", G.vertices[v]);in_queue(Q, v);}while (!isempty_queue(Q)) {int temp = out_queue(Q);for (int i = 0; i < G.vexnum; i++) {if (G.arc[temp][i] != 0 && !visit[i]) {visit[i] = 1;printf("%d ", G.vertices[i]);in_queue(Q, i);}}}
}void BFST(MGraph G, QUEUE* Q)
{printf("\nBFS的遍历:");int i = 0;for (i = 0; i < G.arcnum; i++)visit[i] = 0;for (i = 0; i < G.vexnum; i++) {if (!visit[i]) BFS(G, Q, i);}
}int LocateVex(MGraph G, int v)
{for (int i = 0; i < G.vexnum; i++) {if (G.vertices[i] == v)return i;}return 0;
}void CreatMGraph(MGraph* G)
{int i = 0, j = 0;printf("请分别输入顶点数和边数: \n");scanf("%d%d", &(G->vexnum), &(G->arcnum));printf("请输入顶点信息:\n");for (i = 0; i < G->vexnum; i++)scanf("%d", &(G->vertices[i]));for (i = 0; i < G->vexnum; i++) {for (j = 0; j < G->vexnum; j++)G->arc[i][j] = 0;}printf("请输入构成边的两个顶点: \n");for (i = 0; i < G->arcnum; i++) {int num, num1;scanf("%d%d", &num, &num1);int j = LocateVex(*G, num);int k = LocateVex(*G, num1);G->arc[j][k] = 1;}
}void PrintMGraph(MGraph G)
{printf("*************************\n");printf("邻接矩阵的遍历:\n");for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {printf("%d ", G.arc[i][j]);if (G.arc[i][j] != 0)out_deg[i]++;if (G.arc[j][i] != 0)in_deg[i]++;}printf("\n");}printf("*************************\n");
}void Print_in_out_deg(MGraph G)
{printf("\n*************************\n");printf("各顶点的度的遍历:\n");for (int i = 0; i < G.vexnum; i++) {printf("\n第%d条边的入度: %d 与出度: %d\n", i + 1, in_deg[i], out_deg[i]);}printf("*************************\n");
}void DFS(MGraph G, int v)
{visit[v] = 1;printf("%d ", G.vertices[v]);for (int i = 0; i < G.vexnum; i++) {if (G.arc[v][i] != 0 && visit[i] == 0)DFS(G, i);}
}void DFST(MGraph G)
{printf("DFS的遍历:");for (int i = 0; i < G.vexnum; i++) {if (!visit[i])DFS(G, i);}
}int main()
{MGraph G;QUEUE Q;init_queue(&Q);CreatMGraph(&G);PrintMGraph(G);DFST(G);BFST(G, &Q);Print_in_out_deg(G);return 0;
}
![[保研/考研机试] KY129 简单计算器 浙江大学复试上机题 C++实现](https://img-blog.csdnimg.cn/2397235da5da434d96b767297e4328d8.png)