标题：【leetcode】前缀和

@水墨不写bug

---

正文开始：

（一）简单前缀和

描述

给定一个长度为n的数组a1​,a2​,....an​.

接下来有q次查询, 每次查询有两个参数l, r.

对于每个询问, 请输出al​+al+1​+....+ar​

输入描述：

第一行包含两个整数n和q.

第二行包含n个整数, 表示a1​,a2​,....an​.

接下来q行,每行包含两个整数   l和r.

1≤n,q≤10^5
-10^9≤a[i]≤10^9
1≤l≤r≤n

输出描述：

输出q行,每行代表一次查询的结果.

示例1

输入：

3 2
1 2 4
1 2
2 3

输出：

3
6

         思路一： 暴力求解，时间复杂度O（N^2），看到下方的数据量，显然是会超时的算法；

        思路二：动态规划

        动态规划是一种解决多阶段决策问题的数学优化方法。它将原问题分解为若干个子问题，并把子问题的解保存起来，避免重复计算，从而减少计算量。动态规划通常适用于具有重叠子问题和最优子结构的问题，通过构建一个递推关系式，将问题的最优解表示成子问题的最优解的组合。通过自底向上的方式，从子问题的最优解逐步推导出原问题的最优解。动态规划可以大大提高问题的求解效率，但也需要额外的空间来存储子问题的解。

        通过这一思想，我们可以创建一个dp数组：它的每一个下标i对应的位置存储和它对应下标的arr的前（i）个元素和：

        这时若要求得 [l,r] 闭区间的两个下标之间的元素之和，只需对dp数组操作即可。解题关键就是找到如何构造dp数组的方法，以及如何利用dp数组来得到结果。

        本题构建dp数组的策略比较简单：dp数组的前一项加上arr数组的本项即可得到dp数组的本项:

dp[k] = dp[k-1] + arr[k]

        利用dp数组的方法也很简单：输出dp的r下标和dp的（l - 1）下标之和即可：

cout<<(long)dp[r]-(long)dp[l-1]<<endl;

        时间复杂度O(q);

       

        考虑到题目需要做加法，并且数据量达到10 ^5,数据返回范围达到了10^9量级，所以数据类型开成long。

参考代码： 

#include <iostream>
#include <vector>
using namespace std;
int main() {int n,q;cin>>n>>q;vector<long> arr(n+1);for(int i = 1;i < n+1;i++) cin>>arr[i];vector<long> dp(n+1);//构造数组dpfor(int k = 1;k < n+1;k++) dp[k] = dp[k-1] + arr[k];for(int j = 0;j < q;j++)//主逻辑{int l = 0,r = 0;cin>>l>>r;cout<<(long)dp[r]-(long)dp[l-1]<<endl;}
}

（二）二维前缀和

描述

给你一个 n 行 m 列的矩阵 A ，下标从1开始。

接下来有 q 次查询，每次查询输入 4 个参数 x1 , y1 , x2 , y2

请输出以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和，

输入描述：

第一行包含三个整数n,m,q.

接下来n行，每行m个整数，代表矩阵的元素

接下来q行，每行4个整数x1, y1, x2, y2，分别代表这次查询的参数

1≤n,m≤1000
1≤q≤10^5
−109≤a[i][j]≤10^9
1≤x1​≤x2​≤n
1≤y1​≤y2​≤m

输出描述：

输出q行，每行表示查询结果。

示例1

输入：

3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4

输出：

8
25
32

备注：

读入数据可能很大，请注意读写时间。

         经过了一维前缀和的铺垫，对前缀和有了一些初步理解，在解决二维前缀和就容易多了：

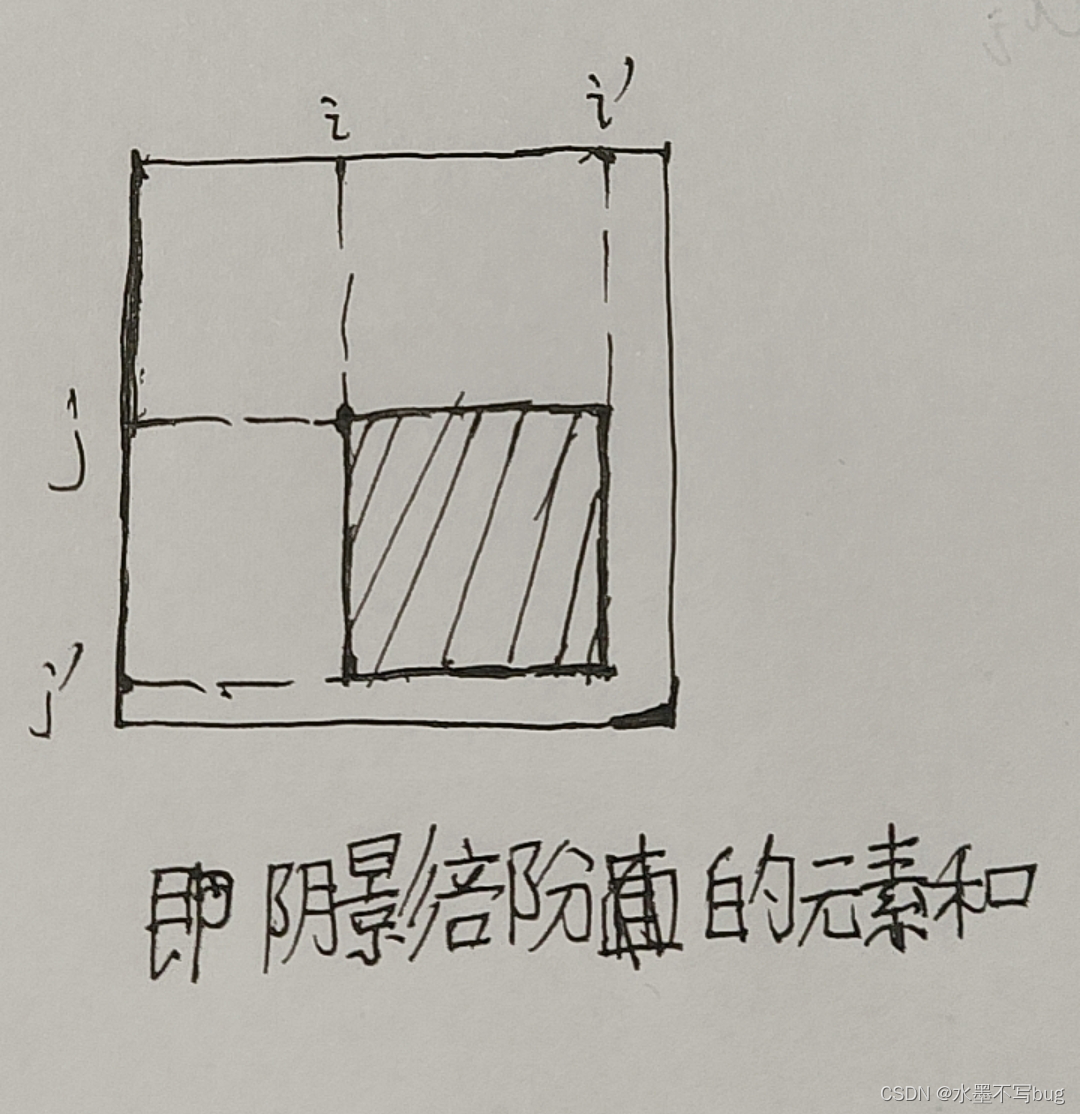
        题目要求是返回两个坐标之间的元素和：

思路一：暴力求解，时间复杂度O（q*N^2），显然是会超时的算法。

 思路二：用动态规划思想，采用二维前缀和方法。

        首先，我们可以定义一个辅助矩阵dp，其中dp[i][j]表示以(1,1)为左上角，(i,j)为右下角的子矩阵的和。

                                （下标为0的行和列不使用）

        接下来，我们可以通过以下方程来计算dp数组：

dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + A[i][j]

        其中，dp[i-1][j]表示以(1,1)为左上角，(i-1,j)为右下角的子矩阵的和； dp[i][j-1]表示以(1,1)为左上角，(i,j-1)为右下角的子矩阵的和； dp[i-1][j-1]表示以(1,1)为左上角，(i-1,j-1)为右下角的子矩阵的和； A[i][j]表示矩阵A的元素。

        对于每次查询(x1, y1)(x2, y2)，我们可以通过如下公式计算子矩阵的和：

sum = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

        其中，dp[x2][y2]表示以(1,1)为左上角，(x2,y2)为右下角的子矩阵的和； dp[x1-1][y2]表示以(1,1)为左上角，(x1-1,y2)为右下角的子矩阵的和； dp[x2][y1-1]表示以(1,1)为左上角，(x2,y1-1)为右下角的子矩阵的和； dp[x1-1][y1-1]表示以(1,1)为左上角，(x1-1,y1-1)为右下角的子矩阵的和。

        其实前缀和是一类题型，我们可以在一定程度上记忆状态转移方程（上述的dp表构建方程，使用dp表方程）， 但是我认为更重要的是理解方程为什么是这样的结构，以及方程的推导由来：

         

参考代码： 

#include <iostream>
#include<vector>
using namespace std;int main(){int n = 0,m = 0,q = 0;cin>>n>>m>>q;vector<vector<int>> arr(n+1,vector<int>(m+1));for(int i = 1;i <= n ; i++)//读取数据for(int j = 1;j <= m ; j++)cin>>arr[i][j];vector<vector<long>> dp(n+1,vector<long>(m+1));//long防止溢出for(int i = 1;i <= n ; i++)//建表for(int j = 1;j <= m ; j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];for(int c = 0;c<q;c++)//c仅仅起计数作用{int i0 = 0,j0 = 0,i = 0,j = 0;cin>>i0>>j0>>i>>j;long ret = dp[i][j] - dp[i][j0-1] - dp[i0-1][j]+dp[i0-1][j0-1];cout<<ret<<endl;}
}
// 64 位输出请用 printf("%lld")

（三）寻找数组的中心下标

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

示例 1：

输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。

示例 2：

输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。

示例 3：

输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0 ，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。

提示：

• 1 <= nums.length <= 10^4
• -1000 <= nums[i] <= 1000

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<long> f(n), g(n);for(int i = 1;i < n;i++)//建f，g表f[i] = f[i-1] + nums[i-1];//不赋值默认为0for(int i = n-2;i >= 0;i--)g[i] = g[i+1] + nums[i+1];for(int k = 0;k < n;k++)if(f[k]==g[k]) return k;return -1;}
};

 （四）除自身外数组的乘积

        给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

        题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

        请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

提示：

• 2 <= nums.length <= 10^5
• -30 <= nums[i] <= 30
• 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n), g(n);f[0] = g[n-1] = 1;//乘法操作不能初始化为0for(int i = 1;i < n;i++)//建f，g表f[i] = f[i-1] * nums[i-1];//不赋值默认为0for(int i = n-2;i >= 0;i--)g[i] = g[i+1] * nums[i+1];vector<int> ret;for(int i = 0;i < n;i++)ret.push_back(f[i]*g[i]);return ret;}
};

---

完~

未经作者同意禁止转载