本篇博客主要是浅谈数据结构概念及时间复杂度,并做长期的维护更新,有需要借鉴即可。
复杂度目录
- 一、初识数据结构
- 1.基础概念
- 2.如何学好数据结构
- 二、复杂度
- 1.复杂度
- 2.时间复杂度
- ①有限数的时间复杂度
- ②函数的时间复杂度
- ③二分查找时间复杂度
- ④递归
- 拓展练习题1:消失的数字
- 3.空间复杂度
- 拓展练习题2:旋转数组
- 拓展练习题③数组,二级指针
- 拓展练习题④移除元素
一、初识数据结构
1.基础概念
数据结构(Data Structure) 是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。简单来说,数据结构就是在内存中管理数据。
相关概念拓展:
算法(Algorithm) 就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。简单来说,算法就是在磁盘中管理数据。
在内存与磁盘中管理数据的区别:
在内存中,
- 数据存储速度比较快(相对磁盘而言)
- 属于带电存储类型
相对应的,在磁盘中,
- 数据存储速度比较慢(相对内存而言)
- 属于不带电存储类型。
思考:带电与不带电存储对存储的影响是什么?
答:存储寿命
如果是需要带电存储,那么就需要不断电,那么也就意味这文件内容不能永久性存储;相应的,如果可以脱离电量进行存储,那么就可以永久性存储在硬件中(这里不考虑硬件寿命问题)。
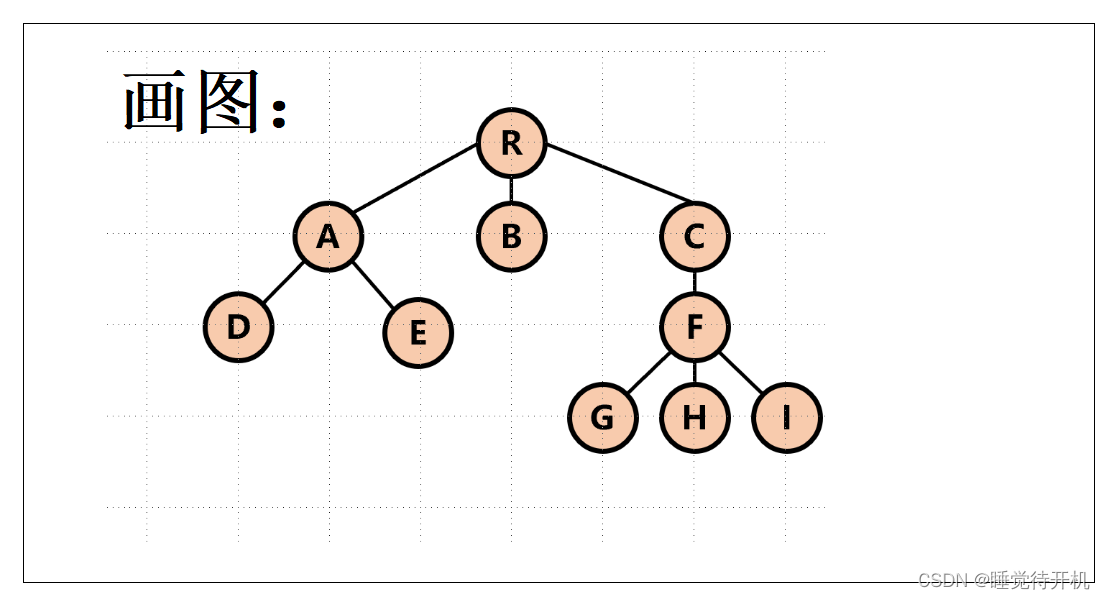
2.如何学好数据结构
- 画图
- 代码练习与思考

二、复杂度
1.复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
元素个数的逐渐增大,复杂度的差异逐渐明显
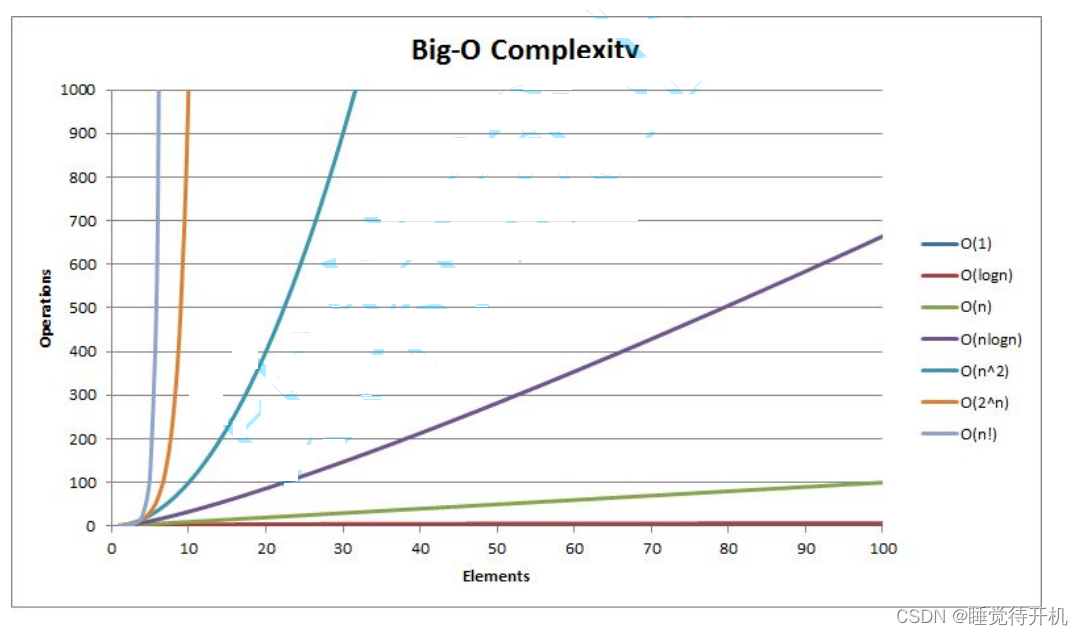
复杂度包括两个方面:
- 时间复杂度
- 空间复杂度
表示方法:
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
- 在实际中一般情况关注的是算法的最坏运行情况。
复杂度的意义何在?
用来衡量/决策比较某一种/多种实现方法的优劣
复杂度是准确的吗?
复杂度是粗略估计,对算法进行大致分“阶级”
2.时间复杂度
算法中的基本操作的执行次数,为算法的时间复杂度。
举例:
①有限数的时间复杂度

②函数的时间复杂度

注strchr:LINK
③二分查找时间复杂度
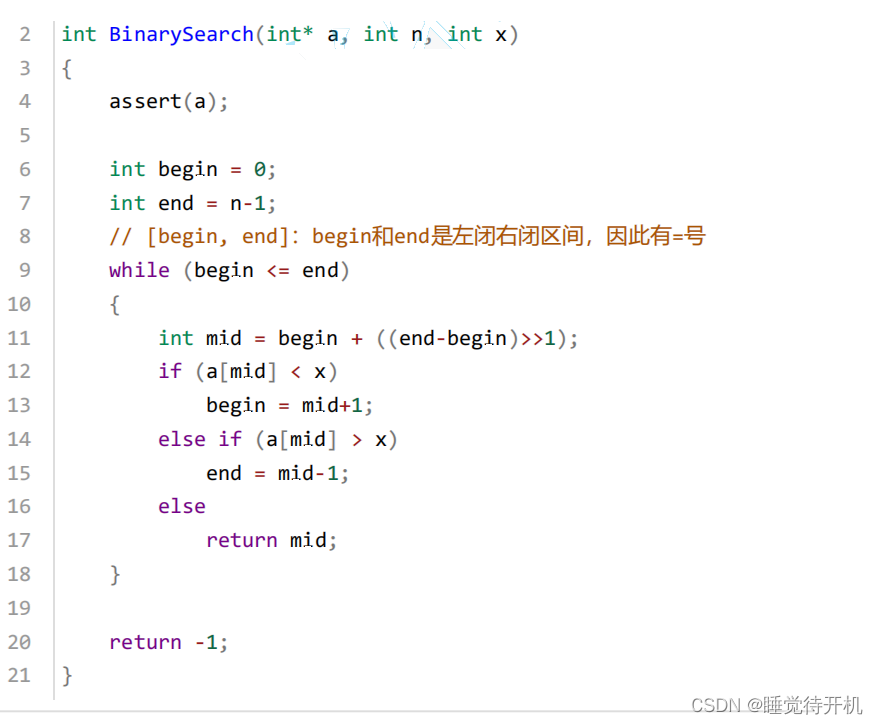
时间复杂度:O(logN)
④递归

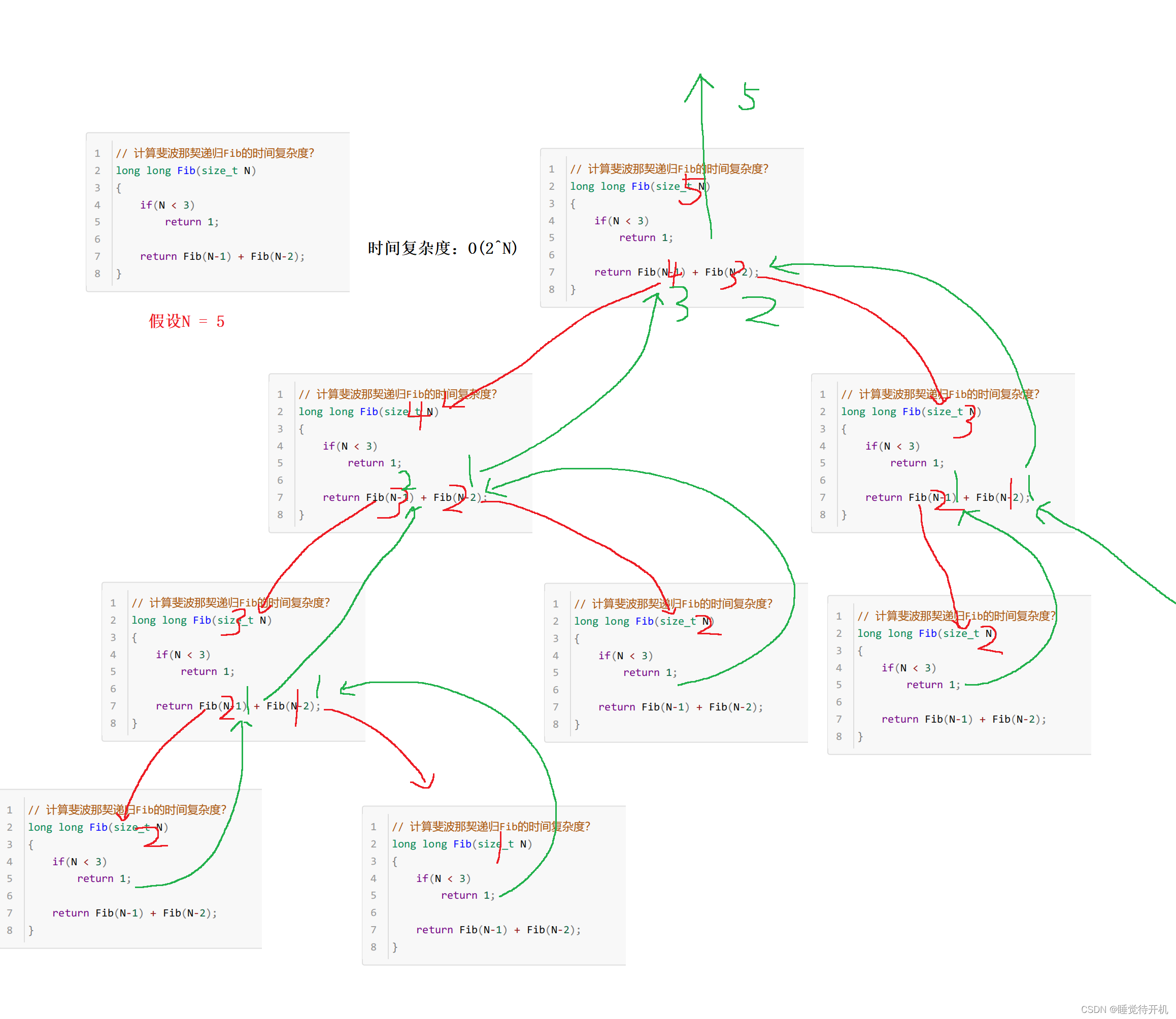
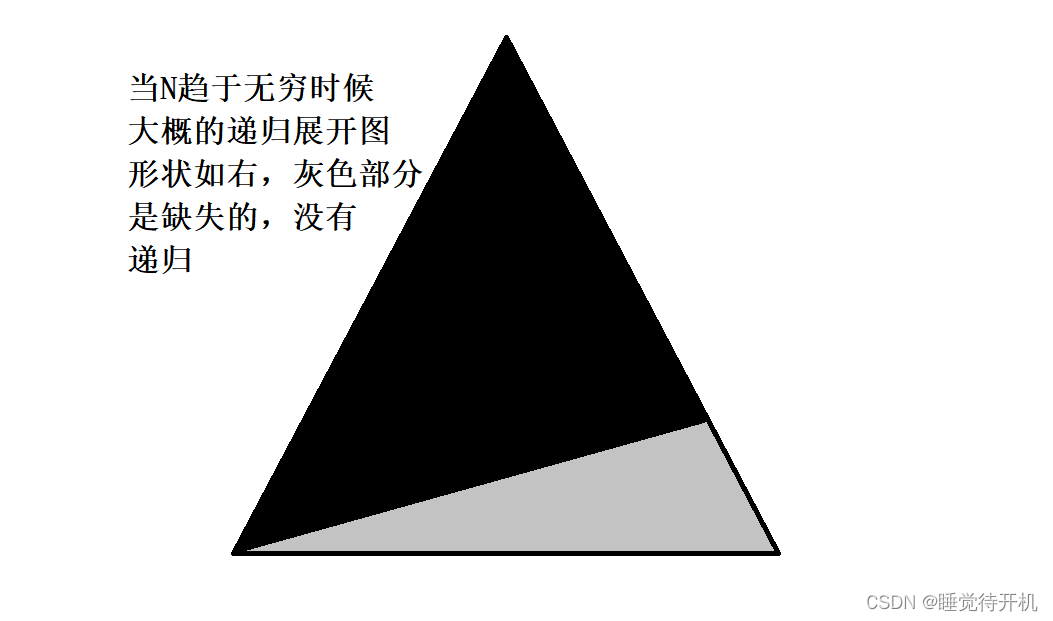
拓展练习题1:消失的数字
消失的数字:LINK
int missingNumber(int* nums, int numsSize){// //思路二:先加起来然后减去,即可得到消失的数字
// int i = 0;
// int lose = 0;
// int sum = 0;
// //加上0到numsSize全部的数字
// for(i = 0;i<numsSize+1;i++)
// {
// sum+=i;
// }
// //减去原数组0到numsSize的数字
// for(i = 0;i<numsSize;i++)
// {
// sum-=nums[i];
// }
// //得到消失的数字
// lose = sum;
// return lose;//思路三:异或操作
int i = 0;
int lose = 0;
//异或正常的数组
for(i = 0;i<numsSize+1;i++)
{lose^=i;
}
//异或原来的数组
for(i = 0;i<numsSize;i++)
{lose^=nums[i];
}
//返回
return lose;
}3.空间复杂度
为了实现某个功能额外开辟的空间。
需要注意的是:时间一去不复返,但是空间可以重复利用滴。
拓展练习题2:旋转数组
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>//旋转数组
void printArray(int arr[],int length)
{for (int i = 0; i < length; i++){printf("%d ", arr[i]);}printf("\n");
}//1.暴力求解
void test1(int arr[],int length,int k)
{while (k--){int temp = arr[length - 1];for (int i = length -1-1; i >= 0; i--){arr[i+1] = arr[i];}arr[0] = temp;}printArray(arr, length);
}void Swap(int arr[],int start,int end)
{while (start < end){int temp = arr[start];arr[start] = arr[end];arr[end] = temp;start++;end--;}}
//2.逆置法
void test2(int arr[], int length, int k)
{//1.首先逆置后半部分Swap(arr,length-k, length-1);printArray(arr, length);//2.其次逆置前半部分Swap(arr, 0, length - k - 1);printArray(arr, length);//3.整个数组进行逆置Swap(arr, 0, length - 1);printArray(arr, length);
}//3.空间换时间方法
void test3(int arr[], int length, int k)
{//开辟空间int* temp = (int*)malloc(sizeof(int) * length);if (temp == NULL){perror("malloc fail");exit(-1);}//拷贝值到新数组中去for (int i = 0,j = k; i <= length - k - 1; i++,j++){temp[j] = arr[i];}for (int i = length - k, j = 0; i <= length - 1; i++, j++){temp[j] = arr[i];}//拷贝回去for (int i = 0; i < length; i++){arr[i] = temp[i];}printArray(arr, length);
}int main()
{int k = 3;int arr[] = { 1,2,3,4,5,6,7 };//test1(arr, sizeof(arr) / sizeof(int), k);//test2(arr, sizeof(arr) / sizeof(int), k);test3(arr, sizeof(arr) / sizeof(int), k);return 0;
}
拓展练习题③数组,二级指针

拓展练习题④移除元素
原题链接:LINK

//三条思路
//1.传统的覆盖
//2.开新数组
//3.双指针
int removeElement(int* nums, int numsSize, int val) {int i = 0;int p1 = 0;//探路者int p2 = 0;//守家者for(i = 0;i<numsSize;i++){if(nums[p1]==val){p1++;}else{nums[p2++] = nums[p1++];}}return p2;
}
#if 1
/*解题思路:1. 设置一个变量count,用来记录nums中值等于val的元素的个数2. 遍历nums数组,对于每个元素进行如下操作:a. 如果num[i]等于val,说明值为val的元素出现了一次,count++b. 如果nums[i]不等于元素,将nums[i]往前搬移count个位置因为nums[i]元素之前出现过count个值等于val的元素,已经被删除了因此次数需要将nums[i]往前搬移3. 返回删除之后新数组中有效元素个数时间复杂度:O(N) 空间复杂度:O(1)*/
int removeElement(int* nums, int numsSize, int val){int count = 0;for(int i = 0; i < numsSize; ++i){if(nums[i] == val){count++;}else{nums[i-count] = nums[i];}}return numsSize - count;
}
#endifEOF