给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

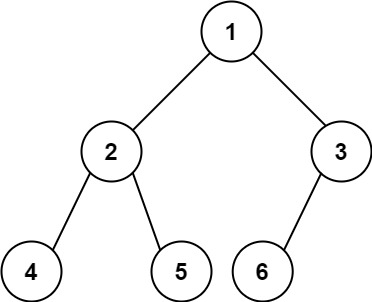
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

方法一 

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*///普通二叉树计算节点数量，后续遍历
class Solution {public int countNodes(TreeNode root) {if(root == null) return 0;int leftcount = countNodes(root.left);int rightcount = countNodes(root.right);return leftcount+rightcount+1;}
}

方法二 

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int countNodes(TreeNode root) {if(root==null) return 0;TreeNode leftnode = root.left;TreeNode rightnode = root.right;int leftnum = 0;int rightnum = 0;//判断是否为满二叉树，可以减少遍历节点的次数while(leftnode!=null){leftnum++;leftnode = leftnode.left;}while(rightnode!=null){rightnum++;rightnode = rightnode.right;}if(rightnum==leftnum){return (2<<leftnum )-1;//满二叉树2^n-1;}return countNodes(root.left)+countNodes(root.right)+1;}
}