The idea behind this algorithm consists in reducing the number of  multiplications at the expense of increasing the number of additions and subtractions. In short, this algorithm uses 7 multiplications and 18 additions of n/2 × n/2 matrices.

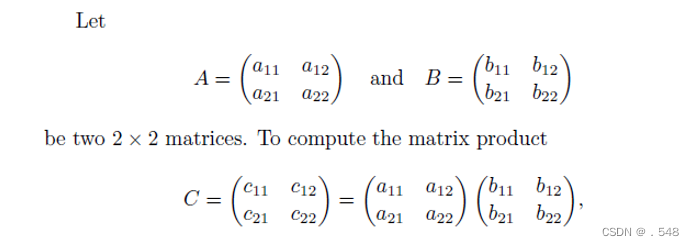
要计算两个复数 x=a+bi 和 y=c+di 的乘积，只使用三次乘法，可以按照以下步骤进行：

1. 计算 p=a×c 和 q=b×d。
2. 使用三次乘法计算 r=(a+b)×(c+d)：r=ac+ad+bc+bd。
3. 乘积的实部为 ac−bd=p−q。
4. 乘积的虚部为 ad+bc=r−p−q。

这种方法可以使用更少的乘法来计算两个复数的乘积，比标准方法（需要四次乘法）更高效。