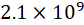本篇为本科课程《电力系统稳态分析》的笔记。
本篇这一章的第二篇笔记。上一篇传送门,下一篇传送门。
三相线路的正序电纳
线路的电导
线路的电导反映的是导线上施加电压后的电晕现象和绝缘子中产生的泄露电流的参数。一般情况线路绝缘良好,泄露电流很小。
电晕只在线路电压超过某一临界值才会发生,这一临界值就是电晕起始电压或电晕临界电压,其相电压近似为:
U c r = 49.3 m 1 m 2 δ r lg D m r (kV) U_{cr}=49.3m_1m_2\delta r \lg\frac{D_m}{r} \quad \text{(kV)} Ucr=49.3m1m2δrlgrDm(kV)
其中, m 1 m_1 m1是导体表面的光滑系数,单股导线为0.831,绞线为0.830.87。 m 2 m_2 m2是气象系数,通常为0.81~1(干燥晴天为1)。 δ \delta δ为空气相对密度。
在一般的电力系统计算中,通常忽略电晕损耗和泄露电流,取 g = 0 g=0 g=0。
线路方程及等值电路
如果将线路用集中参数元件来代替,则可以从两端电压、电流向量之间的关系式导出相应的等值电路。
线路方程
参数沿着线路均匀分布,那么线路的一相电路如图所示在任意一个长度上都有串联阻抗 Δ x ( R 0 + L 0 ) \Delta x(R_0+L_0) Δx(R0+L0)和并联导纳 Δ x ( G 0 + C 0 ) \Delta x(G_0+C_0) Δx(G0+C0)

如图所示,可以根据电压和电流列出式子:
u ( x + Δ x , t ) − u ( x , t ) = Δ x R 0 i ( x + Δ x , t ) + Δ x L 0 ∂ i ( x + Δ x , t ) ∂ T i ( x + Δ x , t ) − i ( x , t ) = Δ x G 0 u ( x , t ) + Δ x C 0 ∂ u ( x , t ) ∂ T u(x+\Delta x,t)-u(x,t)=\Delta x R_0 i(x+\Delta x,t)+\Delta x L_0 \frac{\partial i(x+\Delta x,t)}{\partial T}\\\\ i(x+\Delta x,t)-i(x,t)=\Delta x G_0 u(x,t)+\Delta x C_0 \frac{\partial u(x,t)}{\partial T} u(x+Δx,t)−u(x,t)=ΔxR0i(x+Δx,t)+ΔxL0∂T∂i(x+Δx,t)i(x+Δx,t)−i(x,t)=ΔxG0u(x,t)+ΔxC0∂T∂u(x,t)
将 Δ x \Delta x Δx除到等式的左边,并且令 Δ x → 0 \Delta x \rightarrow0 Δx→0,则:
∂ u ( x , t ) ∂ x = R 0 i ( x , t ) + L 0 ∂ i ( x , t ) ∂ t ∂ i ( x , t ) ∂ x = G 0 u ( x , t ) + C 0 ∂ u ( x , t ) ∂ t \frac{\partial u(x,t)}{\partial x}=R_0 i(x,t)+L_0\frac{\partial i(x,t)}{\partial t}\\\\ \frac{\partial i(x,t)}{\partial x}=G_0 u(x,t)+C_0\frac{\partial u(x,t)}{\partial t} ∂x∂u(x,t)=R0i(x,t)+L0∂t∂i(x,t)∂x∂i(x,t)=G0u(x,t)+C0∂t∂u(x,t)
上述推导的公式,是一般的表达式,既适用于稳态分析,也适用于暂态分析。
而稳态的工频电压表达式为: U ˙ ( x , t ) = 2 U ( x ) sin ( ω t + ϕ ( x ) ) \dot{U}(x,t)=\sqrt{2}U(x)\sin(\omega t+\phi(x)) U˙(x,t)=2U(x)sin(ωt+ϕ(x)),即 U ˙ ( x ) = U ( x ) ∠ ϕ ( x ) \dot{U}(x)=U(x)\angle \phi(x) U˙(x)=U(x)∠ϕ(x)。
将电压对时间求偏导可得: ∂ U ˙ ( x ) ∂ t = j ω U ˙ ( x ) \frac{\partial \dot{U}(x)}{\partial t}=j\omega \dot{U}(x) ∂t∂U˙(x)=jωU˙(x)。
对于稳态电流的处理也是相同的过程。
那么就可以把上述微分方程化为:
d U ˙ ( x ) d x = R 0 I ˙ ( x ) + j ω L 0 I ˙ ( x ) = z 0 I ˙ ( x ) d I ˙ ( x ) d x = G 0 U ˙ ( x ) + j ω C 0 U ˙ ( x ) = y 0 U ˙ ( x ) \frac{\mathrm{d} \dot{U}(x)}{\mathrm{d} x}=R_0 \dot{I}(x)+j\omega L_0 \dot{I}(x)=z_0\dot{I}(x)\\\\ \frac{\mathrm{d} \dot{I}(x)}{\mathrm{d} x}=G_0 \dot{U}(x)+j\omega C_0 \dot{U}(x)=y_0\dot{U}(x) dxdU˙(x)=R0I˙(x)+jωL0I˙(x)=z0I˙(x)dxdI˙(x)=G0U˙(x)+jωC0U˙(x)=y0U˙(x)
这个微分方程电压和电流时耦合在一起的,需要解耦,那么两边同时再求一次关于x的导数,可得:
d 2 U ˙ ( x ) d x 2 = z 0 d I ˙ ( x ) d x = z 0 y 0 U ˙ ( x ) d 2 I ˙ ( x ) d x 2 = y 0 d U ˙ ( x ) d x = z 0 y 0 I ˙ ( x ) \frac{\mathrm{d}^2 \dot{U}(x)}{\mathrm{d} x^2}=z_0\frac{\mathrm{d} \dot{I}(x)}{\mathrm{d} x}=z_0 y_0\dot{U}(x)\\\\ \frac{\mathrm{d}^2 \dot{I}(x)}{\mathrm{d} x^2}=y_0\frac{\mathrm{d} \dot{U}(x)}{\mathrm{d} x}=z_0 y_0\dot{I}(x) dx2d2U˙(x)=z0dxdI˙(x)=z0y0U˙(x)dx2d2I˙(x)=y0dxdU˙(x)=z0y0I˙(x)
得到参数 ρ 2 = z 0 y 0 \rho^2=z_0y_0 ρ2=z0y0,那么 ρ = ± z 0 y 0 = ± Γ \rho=\pm\sqrt{z_0y_0}=\pm\Gamma ρ=±z0y0=±Γ,即 Γ = z 0 y 0 \Gamma =\sqrt{z_0y_0} Γ=z0y0,这是传播系数,也是一个复数,值 Γ = α + β \Gamma =\alpha+\beta Γ=α+β, α \alpha α称为衰减系数,而 β \beta β称为移相系数。
可以解出电压和电流的通解为:
U ˙ ( x ) = C 1 e Γ x + C 2 e − Γ x I ˙ ( x ) = 1 z 0 d U ˙ ( x ) d x = Γ z 0 ( C 1 e Γ x − C 2 e − Γ x ) \dot{U}(x)=C_1e^{\Gamma x}+C_2e^{-\Gamma x}\\\\ \dot{I}(x)=\frac{1}{z_0}\frac{\mathrm{d} \dot{U}(x)}{\mathrm{d} x}=\frac{\Gamma}{z_0}(C_1e^{\Gamma x}-C_2e^{-\Gamma x}) U˙(x)=C1eΓx+C2e−ΓxI˙(x)=z01dxdU˙(x)=z0Γ(C1eΓx−C2e−Γx)
定义 z c = z 0 y 0 = z 0 Γ z_c=\sqrt{\frac{z_0}{y_0}}=\frac{z_0}{\Gamma} zc=y0z0=Γz0为线路的特征阻抗或波阻抗。那么可以重新书写电流的通解:
I ˙ ( x ) = 1 z c ( C 1 e Γ x − C 2 e − Γ x ) \dot{I}(x)=\frac{1}{z_c}(C_1e^{\Gamma x}-C_2e^{-\Gamma x}) I˙(x)=zc1(C1eΓx−C2e−Γx)
实际中想要确定常数的值,需要用到线路末端x=0,即最右端处的边界条件 U ˙ ( 0 ) = U ˙ 2 , I ˙ ( 0 ) = I ˙ 2 \dot{U}(0)=\dot{U}_2,\dot{I}(0)=\dot{I}_2 U˙(0)=U˙2,I˙(0)=I˙2,带入式中,解得:
C 1 = U ˙ 2 + z c I ˙ 2 2 C 2 = U ˙ 2 − z c I ˙ 2 2 C_1=\frac{\dot{U}_2+z_c\dot{I}_2}{2}\\\\ C_2=\frac{\dot{U}_2-z_c\dot{I}_2}{2} C1=2U˙2+zcI˙2C2=2U˙2−zcI˙2
再将解得的常数带回方程通解,得到特解,并利用双曲函数导出:
U ˙ ( x ) = U ˙ 2 cosh Γ x + I ˙ 2 Z c sinh Γ x I ˙ ( x ) = U ˙ 2 z c sinh Γ x + I ˙ 2 cosh Γ x \dot{U}(x)=\dot{U}_{2}\cosh\Gamma x+\dot{I}_{2}Z_{c}\sinh\Gamma x \\ \dot{I}(x)=\frac{\dot{U}_{2}}{z_{c}}\sinh\Gamma x+\dot{I}_{2}\cosh\Gamma x U˙(x)=U˙2coshΓx+I˙2ZcsinhΓxI˙(x)=zcU˙2sinhΓx+I˙2coshΓx
这就是已知末端电压电流的情况下,线路任意处的电压和电流的表达式。
-
令x=l,也就是带入线路始端即最左端的坐标,得到起始端的电压 U ˙ 1 \dot{U}_{1} U˙1和电流 I ˙ 1 \dot{I}_{1} I˙1,线路两端的电流电压关系式是:
U ˙ 1 = U ˙ 2 cosh Γ l + I ˙ 2 z c sinh Γ l I ˙ 1 = U ˙ 2 z c sinh Γ l + I ˙ 2 cosh Γ l \begin{equation} \begin{aligned} \dot{U}_1=\dot{U}_2\cosh{\Gamma}l+\dot{I}_2z_c\sinh{\Gamma}l\\ \dot{I}_1=\frac{\dot{U}_2}{z_c}\sinh{\Gamma}l+\dot{I}_2\cosh{\Gamma}l \end{aligned} \end{equation} U˙1=U˙2coshΓl+I˙2zcsinhΓlI˙1=zcU˙2sinhΓl+I˙2coshΓl -
当末端接一个阻抗 z L = z c z_L=z_c zL=zc时, U ˙ 2 = z c I ˙ 2 = z L I ˙ 2 \dot{U}_2=z_c\dot{I}_2=z_L\dot{I}_2 U˙2=zcI˙2=zLI˙2, U ˙ ( x ) = U ˙ 2 cosh Γ x + I ˙ 2 Z c sinh Γ x = e α x U ˙ 2 ∠ ( ϕ 2 + β x ) \dot{U}(x)=\dot{U}_{2}\cosh\Gamma x+\dot{I}_{2}Z_{c}\sinh\Gamma x=e^{\alpha x}\dot{U}_2\angle(\phi_2+\beta x) U˙(x)=U˙2coshΓx+I˙2ZcsinhΓx=eαxU˙2∠(ϕ2+βx)
线路的自然功率
令线路的 R 0 = 0 R_0=0 R0=0和 G 0 = 0 G_0=0 G0=0,成为了无损耗线路,其波阻抗 z c = z 0 y 0 = L 0 C 0 z_c=\sqrt{\frac{z_0}{y_0}}=\sqrt{\frac{L_0}{C_0}} zc=y0z0=C0L0为纯电阻。
在线路末端为纯有功功率,其值为:
S ~ z = 3 U ˙ 2 ( U ˙ 2 3 z c ) ∗ = U 2 2 z c \widetilde{S}_z=\sqrt{3}\dot{U}_2(\frac{\dot{U}_2}{\sqrt{3}z_c})^*=\frac{U_2^2}{z_c} S z=3U˙2(3zcU˙2)∗=zcU22
这个值也被称为线路的自然功率 P e P_e Pe,是一个固有的参数,在线路的任意一点 S ~ ( x ) = 3 U ˙ ( x ) I ˙ ( x ) \widetilde{S}(x)=\sqrt{3}\dot{U}(x)\dot{I}(x) S (x)=3U˙(x)I˙(x)均等于自然功率。
传播系数 Γ = j β = z 0 y 0 = j ω L 0 C 0 \Gamma=j\beta=\sqrt{z_0y_0}=j\omega L_0 C_0 Γ=jβ=z0y0=jωL0C0,可见没有实数部分即 α = 0 \alpha=0 α=0。可以导出任意一点的电压电流值:
U ˙ ( x ) = U ˙ 2 ( cos β x + j sin β x ) = U ˙ 2 e j β x I ˙ ( x ) = I ˙ 2 ( cos β x + j sin β x ) = I ˙ 2 e j β x \dot{U}(x)=\dot{U}_2(\cos\beta x+j\sin\beta x)=\dot{U}_2e^{j\beta x}\\\\ \dot{I}(x)=\dot{I}_2(\cos\beta x+j\sin\beta x)=\dot{I}_2e^{j\beta x} U˙(x)=U˙2(cosβx+jsinβx)=U˙2ejβxI˙(x)=I˙2(cosβx+jsinβx)=I˙2ejβx
同一点的电流电压同相位,即任意点的无功功率都为0。
线路传输的波速推导:
U ˙ ( x ) = e Γ x U ˙ 2 + z c I ˙ 2 2 + e − Γ x U ˙ 2 − z c I ˙ 2 2 = U ˙ + ( x ) + U ˙ − ( x ) \dot{U}(x)=e^{\Gamma x}\frac{\dot{U}_2+z_c\dot{I}_2}{2}+e^{-\Gamma x}\frac{\dot{U}_2-z_c\dot{I}_2}{2}=\dot{U}_+(x)+\dot{U}_-(x) U˙(x)=eΓx2U˙2+zcI˙2+e−Γx2U˙2−zcI˙2=U˙+(x)+U˙−(x)
将电压波可以分解成两个波,一个 U ˙ + ( x ) \dot{U}_+(x) U˙+(x)正向转播,一个 U ˙ − ( x ) \dot{U}_-(x) U˙−(x)反向传播。
对于 U ˙ + ( x ) \dot{U}_+(x) U˙+(x),有:
U ˙ + ( x ) = e j β x ∣ C 1 ∣ ∠ θ = ∣ C 1 ∣ ∠ ( θ + β x ) \dot{U}_+(x)=e^{j\beta x}|C_1|\angle \theta=|C_1|\angle (\theta+\beta x) U˙+(x)=ejβx∣C1∣∠θ=∣C1∣∠(θ+βx)
将 U ˙ + ( x ) \dot{U}_+(x) U˙+(x)写成三角函数的形式:
U + ( x , t ) = 2 ∣ C 1 ∣ sin ( ω t + θ + β x ) U_+(x,t)=\sqrt{2}|C_1|\sin(\omega t+\theta+\beta x) U+(x,t)=2∣C1∣sin(ωt+θ+βx)
令 ω t + θ + β x = 0 \omega t+\theta+\beta x=0 ωt+θ+βx=0也就是波峰的位置,解得 x = ω β t + C x=\frac{\omega}{\beta}t+C x=βωt+C,C是常数。
波峰移动的速度就是波传播的速度: v = d x d t = ω β = ω ω L 0 C 0 = 1 L 0 C 0 v=\frac{\mathrm{d}x}{\mathrm{d}t}=\frac{\omega}{\beta}=\frac{\omega}{\omega\sqrt{L_0C_0}}=\frac{1}{\sqrt{L_0C_0}} v=dtdx=βω=ωL0C0ω=L0C01
根据本章前文给出的电网阻抗和导纳计算公式,可以将他们相乘:
X B = 0.1445 lg D m r × 7.58 × 1 0 − 6 D m r = ω L 0 ω C 0 = ω 2 L 0 C 0 = ( 100 π ) 2 L 0 C 0 ⇒ 0.1445 × 7.58 × 1 0 − 6 = ( 100 π ) 2 L 0 C 0 XB=0.1445\lg\frac{D_m}{r}\times\frac{7.58\times10^{-6}}{\frac{D_m}{r}}=\omega L_0 \omega C_0=\omega^2 L_0 C_0=(100\pi)^2L_0C_0\\\\ \Rightarrow 0.1445\times 7.58\times10^{-6}=(100\pi)^2L_0C_0 XB=0.1445lgrDm×rDm7.58×10−6=ωL0ωC0=ω2L0C0=(100π)2L0C0⇒0.1445×7.58×10−6=(100π)2L0C0
所以 v = 1 L 0 C 0 = 100 π 0.1445 × 7.58 × 1 0 − 6 ≈ 3 × 1 0 5 km/s v=\frac{1}{\sqrt{L_0C_0}}=\frac{100\pi}{\sqrt{0.1445\times 7.58\times10^{-6}}}\approx3\times 10^{5}\quad \text{km/s} v=L0C01=0.1445×7.58×10−6100π≈3×105km/s
β = X B = 1.05 × 1 0 − 3 (rad/km) ≈ 0.06 (deg/km) \beta=\sqrt{XB}=1.05\times10^{-3}\text{(rad/km)}\approx0.06\text{(deg/km)} β=XB=1.05×10−3(rad/km)≈0.06(deg/km),也就是每100km相角改变 6 ° 6\degree 6°。
线路的等值电路
将线路的两端,即起始端和末端的电压关系可以写成下面的矩阵形式:
[ U ˙ 1 I ˙ 1 ] = [ cosh Γ l z c sinh Γ l 1 z c sinh Γ l cosh Γ l ] = [ U ˙ 2 I ˙ 2 ] \begin{bmatrix}\dot{U}_1\\\\ \dot{I}_1\end{bmatrix}= \begin{bmatrix}\cosh\Gamma l&z_c\sinh\Gamma l\\\\ \frac{1}{z_c}\sinh\Gamma l&\cosh\Gamma l\end{bmatrix}= \begin{bmatrix}\dot{U}_2\\\\ \dot{I}_2\end{bmatrix} U˙1I˙1 = coshΓlzc1sinhΓlzcsinhΓlcoshΓl = U˙2I˙2
可以把他看成无源的两端口网络,且可以用两端口网络的传输参数 A , B , C , D A,B,C,D A,B,C,D表示为:
[ U ˙ 1 I ˙ 1 ] = [ A B C D ] = [ U ˙ 2 I ˙ 2 ] \begin{bmatrix}\dot{U}_1\\\\ \dot{I}_1\end{bmatrix}= \begin{bmatrix}A&B\\\\ C&D\end{bmatrix}= \begin{bmatrix}\dot{U}_2\\\\ \dot{I}_2\end{bmatrix} U˙1I˙1 = ACBD = U˙2I˙2
对于这样的无源二端口网络,可以使用 Π \Pi Π形或 T \text{T} T等值电路代替。实际中, Π \Pi Π形等值电路比较常见。

如图所示为线路的 Π \Pi Π形等值电路,可以导出两端的电压电流关系:
U ˙ 1 = ( 1 + Z L Y L 2 ) U ˙ 2 + Z L I ˙ 2 I ˙ 1 = Y L ( 1 + Z L Y L 4 ) U ˙ 2 + ( 1 + Z L Y L 2 ) I ˙ 2 \dot{U}_1=\left(1+\frac{Z_LY_L}{2}\right)\dot{U}_2+Z_L\dot{I}_2\\\\ \dot{I}_1=Y_L\left(1+\frac{Z_LY_L}{4}\right)\dot{U}_2+\left(1+\frac{Z_LY_L}{2}\right)\dot{I}_2 U˙1=(1+2ZLYL)U˙2+ZLI˙2I˙1=YL(1+4ZLYL)U˙2+(1+2ZLYL)I˙2
因为等效二端口网络和线路方程描述的是一个系统,所以将上式和上文所述式(1)的两端电流电压关系式相对比,可得:
1 + Z L Y L 2 = cosh Γ l Z L = z c sinh Γ l Y L ( 1 + Z L Y L 4 ) = 1 z c sinh Γ l 1+\frac{Z_LY_L}{2}=\cosh\Gamma l\\\\ Z_L=z_c\sinh\Gamma l\\\\ Y_L\left(1+\frac{Z_LY_L}{4}\right)=\frac{1}{z_c}\sinh\Gamma l 1+2ZLYL=coshΓlZL=zcsinhΓlYL(1+4ZLYL)=zc1sinhΓl
从而可以推出 Π \Pi Π形等值电路的各个参数:
Z L = z c sinh Γ l = z c Γ l sinh Γ l Γ l = z 0 y 0 z 0 y 0 l sinh Γ l Γ l = z 0 l sinh Γ l Γ l Y L = 1 z c 2 ( cosh Γ l − ) sinh Γ l = y 0 tanh Γ l 2 Γ l 2 Z_L=z_c\sinh\Gamma l=z_c\Gamma l\frac{\sinh\Gamma l}{\Gamma l}=\sqrt{\frac{z_0}{y_0}}\sqrt{z_0y_0}l\frac{\sinh\Gamma l}{\Gamma l}=z_0l\frac{\sinh\Gamma l}{\Gamma l}\\\\ Y_L=\frac{1}{z_c}\frac{2(\cosh \Gamma l-)}{\sinh \Gamma l}=y_0\frac{\tanh\frac{\Gamma l}{2}}{\frac{\Gamma l}{2}} ZL=zcsinhΓl=zcΓlΓlsinhΓl=y0z0z0y0lΓlsinhΓl=z0lΓlsinhΓlYL=zc1sinhΓl2(coshΓl−)=y02Γltanh2Γl
z 0 , y 0 z_0,y_0 z0,y0就是线路的阻抗和导纳参数。这样,就把线路的参数化成了无空间信息的集总参数。
对于长度不大于300km,电压低于220kV的输电线路,可以近似的将 Z L , Y L Z_L,Y_L ZL,YL直接取成 z 0 , y 0 z_0,y_0 z0,y0。对于较长的线路,常常使用系数修正或级数分解的方法。
变压器的数学模型
变压器的结构有很多,除了有双绕组变压器、三绕组变压器和自耦变压器,还可以按照构成的情况不同,分为单相变压器组和三相变压器。还有分类分为箱式变压器和组式变压器。
双绕组变压器的等值电路
根据电机学的内容,可得双绕组变压器的T型等值电路,如图所示:

图中的参数,是将2次侧的参数折算到1次侧的参数。
因为变压器励磁阻抗比变压器的楼阻抗大得多,所以并联支路电流很小,可以简化为 Γ \Gamma Γ型等值电路,如图所示:

图中参数 R T = R T 1 + R T 2 ′ , X T = X T 1 + X T 2 ′ R_T=R_{T1}+R'_{T2},X_T=X_{T1}+X'_{T2} RT=RT1+RT2′,XT=XT1+XT2′, G T , B T G_T,B_T GT,BT是由变压器提供的短路试验和空载实验得到的,或者由实际实验计算而来。
变压器出厂铭牌会提供:额定变比 U 1 N U 2 N \frac{U_{1N}}{U_{2N}} U2NU1N,额定容量 S N S_N SN,短路电压百分数 U k % U_k\% Uk%,短路损耗 P k ( k W ) P_k\mathrm{(kW)} Pk(kW),空载电流百分比 I 0 % I_0\% I0%,空载损耗 P 0 ( k W ) P_0\mathrm{(kW)} P0(kW)。
空载实验和变压器等值电路中的电导和电纳
即开路实验,在一侧施加额定电压,另一侧开路,可以测出有功功率损耗 P 0 P_0 P0和空载电流百分比 I 0 % I_0\% I0%。
空载电流很小,所以在变压器绕组引起的铜耗很小,可以略去。将 P 0 P_0 P0视为铁耗即不变损耗,是有功功率损耗。此时的 P 0 P_0 P0采用的是通用单位kW,所以要换算除以1000一变成国际单位制:
P 0 1000 = 3 U I = 3 U N ( U N G T 3 ) = U N 2 G T \frac{P_0}{1000}=\sqrt{3}UI=\sqrt{3}U_N(\frac{U_N G_T}{\sqrt{3}})=U_N^2G_T 1000P0=3UI=3UN(3UNGT)=UN2GT
可以推出 G T = P 0 1000 U N 2 = P 0 1000 S N ( S N U N 2 ) G_T=\frac{P_0}{1000U^2_N}=\frac{P_0}{1000S_N}\left(\frac{S_N}{U^2_N}\right) GT=1000UN2P0=1000SNP0(UN2SN)。
可以近似的认为空载电流 I 0 I_0 I0全部流过了 B T B_T BT支路,所以有:
I 0 % = I 0 I N × 100 = U N B T 3 × 1 I N × 100 = U N 2 S N B T × 100 I_0\%=\frac{I_0}{I_N}\times100=\frac{U_N B_T}{\sqrt{3}}\times\frac{1}{I_N}\times100=\frac{U^2_N}{S_N}B_T\times100 I0%=INI0×100=3UNBT×IN1×100=SNUN2BT×100
考虑到铁芯是感性的,所以其导纳是负数:
B T = − I 0 % 100 ( S N U N 2 ) B_T=-\frac{I_0\%}{100}\left(\frac{S_N}{U^2_N}\right) BT=−100I0%(UN2SN)
短路试验和变压器等值电路中的电阻和电抗
试验中逐渐增加外施电压使得电流达到额定电流 I N I_N IN,这个时候测得的三相小号总有功功率是短路损耗 P k P_k Pk,流经励磁回路的电路太小可以忽略不计,所以也为铜耗,属于可变损耗。测得外施电压为短路电压 U k U_k Uk。
下面是 P k P_k Pk,采用的是通用单位kW,所以要换算除以1000一变成国际单位制:
P k 1000 = 3 I N 2 R T = 3 ( S N 3 U N ) 2 R T = S N 2 U N 2 R T \frac{P_k}{1000}=3I^2_NR_T=3\left(\frac{S_N}{\sqrt{3}U_N}\right)^2R_T=\frac{S^2_N}{U^2_N}R_T 1000Pk=3IN2RT=3(3UNSN)2RT=UN2SN2RT
可以推出: R T = P + k 1000 S N S N 2 U N 2 R_T=\frac{P+k}{1000S_N}\frac{S^2_N}{U^2_N} RT=1000SNP+kUN2SN2。
短路电压 U k U_k Uk和 X T X_T XT上的电压降基本相等:
U k % = U k U N × 100 = 3 I N X T U N × 100 = S N U N 2 X T × 100 U_k\%=\frac{U_k}{U_N}\times100=\frac{\sqrt{3}I_NX_T}{U_N}\times100=\frac{S_N}{U^2_N}X_T\times100 Uk%=UNUk×100=UN3INXT×100=UN2SNXT×100
得到阻抗:
X T = U k % 100 U k 2 S N X_T=\frac{U_k\%}{100}\frac{U^2_k}{S_N} XT=100Uk%SNUk2
不达到额定电路的短路试验
增加外施电压到 U k ′ U'_k Uk′,电流并不是额定电路,而是 α I k \alpha I_k αIk,此时的损耗:
P k ′ = 3 ( α I k ) 2 = α 2 P k P'_k=3(\alpha I_k)^2=\alpha^2 P_k Pk′=3(αIk)2=α2Pk
所以可得:
P k = 1 α 2 P k ′ P_k=\frac{1}{\alpha^2}P'_k Pk=α21Pk′
因为 U k ′ % = U k ′ U N × 100 U'_k\%=\frac{U'_k}{U_N}\times100 Uk′%=UNUk′×100,所以有:
U k ′ = U k ′ % 100 U N U'_k=\frac{U'_k\%}{100}U_N Uk′=100Uk′%UN
又因为 U k = α U k ′ U_k=\alpha U'_k Uk=αUk′,所以有:
U k % = 1 α U k ′ % U_k\%=\frac{1}{\alpha}U'_k\% Uk%=α1Uk′%
当很小的时候,难以精确地测量,当很大的时候,铁芯又会饱和。
参数总结
B T = I 0 % 100 S N U N 2 ( S ) X T = U k % 100 U N 2 S N ( Ω ) G T = P 0 1000 S N S N U N 2 ( S ) R T = P k 1000 S N U N 2 S N ( Ω ) P k = 1 α 2 P k ′ U k % = 1 α U k ′ % B_T=\frac{I_0\%}{100}\frac{S_N}{U^2_N}\quad \mathrm{(S)}\\\\ X_T=\frac{U_k\%}{100}\frac{U^2_N}{S_N}\quad \mathrm{(\Omega)}\\\\ G_T=\frac{P_0}{1000S_N}\frac{S_N}{U^2_N}\quad \mathrm{(S)}\\\\ R_T=\frac{P_k}{1000S_N}\frac{U^2_N}{S_N}\quad \mathrm{(\Omega)}\\\\ P_k=\frac{1}{\alpha^2}P'_k\\\\ U_k\%=\frac{1}{\alpha}U'_k\% BT=100I0%UN2SN(S)XT=100Uk%SNUN2(Ω)GT=1000SNP0UN2SN(S)RT=1000SNPkSNUN2(Ω)Pk=α21Pk′Uk%=α1Uk′%
三绕组变压器等值电路
由电机学内容可知,三绕组变压器等值电路如图所示。其中2,3侧的参数也需要折算到1次侧。

为了适应各侧对绕组容量的不同要求,三侧绕组的额定容量可能是不同的,一共有三类变压器:
- 额定容量比为100/100/100。其三侧绕组的额定容量都等于变压器的额定容量,也就是 S N = 3 U 1 N I 1 N = 3 U 2 N I 2 N = 3 U 3 N I 3 N S_N=\sqrt{3}U_{1N}I_{1N}=\sqrt{3}U_{2N}I_{2N}=\sqrt{3}U_{3N}I_{3N} SN=3U1NI1N=3U2NI2N=3U3NI3N,一般用于升压变压器。
- 额定容量比为100/100/50。跟第一类相比3侧的导线截面少了一半,其额定容量也少了一半。一般用于3侧的负荷小于1、2侧的厂站。
- 额定容量比为100/100/50。一般用于2侧的负荷小于1、3侧的厂站。
下面介绍如何确定三绕组的变压器的参数。
短路试验
对于第一类变压器,可以将三个绕组的出口依次两两短接,做出三回短路试验,测得对应两侧绕组的短路损耗之和:
P k ( 1 , 2 ) = P k 1 + P k 2 P k ( 1 , 3 ) = P k 1 + P k 3 P k ( 2 , 3 ) = P k 2 + P k 3 P_{k(1,2)}=P_{k1}+P_{k2}\\\\ P_{k(1,3)}=P_{k1}+P_{k3}\\\\ P_{k(2,3)}=P_{k2}+P_{k3} Pk(1,2)=Pk1+Pk2Pk(1,3)=Pk1+Pk3Pk(2,3)=Pk2+Pk3
其中, P k ( 1 , 2 ) , P k ( 1 , 3 ) , P k ( 2 , 3 ) P_{k(1,2)},P_{k(1,3)},P_{k(2,3)} Pk(1,2),Pk(1,3),Pk(2,3)是两两绕组间由短路试验得到的短路损耗, P k 1 , P k 2 , P k 3 P_{k1},P_{k2},P_{k3} Pk1,Pk2,Pk3分别是三侧绕组在额定电路下的铜耗。
可以解出每一侧绕组的短路损耗为:
P k 1 = 1 2 ( P k ( 1 , 2 ) + P k ( 1 , 3 ) − P k ( 2 , 3 ) ) P k 2 = 1 2 ( P k ( 1 , 2 ) + P k ( 2 , 3 ) − P k ( 1 , 3 ) ) P k 3 = 1 2 ( P k ( 1 , 3 ) + P k ( 2 , 3 ) − P k ( 1 , 2 ) ) P_{k1}=\frac{1}{2}( P_{k(1,2)}+P_{k(1,3)}-P_{k(2,3)})\\\\ P_{k2}=\frac{1}{2}( P_{k(1,2)}+P_{k(2,3)}-P_{k(1,3)})\\\\ P_{k3}=\frac{1}{2}( P_{k(1,3)}+P_{k(2,3)}-P_{k(1,2)}) Pk1=21(Pk(1,2)+Pk(1,3)−Pk(2,3))Pk2=21(Pk(1,2)+Pk(2,3)−Pk(1,3))Pk3=21(Pk(1,3)+Pk(2,3)−Pk(1,2))
那么就可以推出各侧绕组的电阻为:
R T 1 = P k 1 1000 S N U N 2 S N R T 2 = P k 2 1000 S N U N 2 S N R T 3 = P k 3 1000 S N U N 2 S N R_{T1}=\frac{P_{k1}}{1000S_N}\frac{U^2_N}{S_N}\\\\ R_{T2}=\frac{P_{k2}}{1000S_N}\frac{U^2_N}{S_N}\\\\ R_{T3}=\frac{P_{k3}}{1000S_N}\frac{U^2_N}{S_N} RT1=1000SNPk1SNUN2RT2=1000SNPk2SNUN2RT3=1000SNPk3SNUN2
根据两两绕组间的短路电压百分比数 U k ( 1 , 2 ) % , U k ( 1 , 3 ) % , U k ( 2 , 3 ) % U_{k(1,2)}\%,U_{k(1,3)}\%,U_{k(2,3)}\% Uk(1,2)%,Uk(1,3)%,Uk(2,3)%,可以通过同样的方法求出每一个绕组的短路电压百分数:
U k 1 % = 1 2 ( U k ( 1 , 2 ) % + U k ( 1 , 3 ) % − U k ( 2 , 3 ) % ) U k 2 % = 1 2 ( U k ( 1 , 2 ) % + U k ( 2 , 3 ) % − U k ( 1 , 3 ) % ) U k 3 % = 1 2 ( U k ( 1 , 3 ) % + U k ( 2 , 3 ) % − U k ( 1 , 2 ) % ) U_{k1}\%=\frac{1}{2}(U_{k(1,2)}\%+U_{k(1,3)}\%-U_{k(2,3)}\%)\\\\ U_{k2}\%=\frac{1}{2}(U_{k(1,2)}\%+U_{k(2,3)}\%-U_{k(1,3)}\%)\\\\ U_{k3}\%=\frac{1}{2}(U_{k(1,3)}\%+U_{k(2,3)}\%-U_{k(1,2)}\%) Uk1%=21(Uk(1,2)%+Uk(1,3)%−Uk(2,3)%)Uk2%=21(Uk(1,2)%+Uk(2,3)%−Uk(1,3)%)Uk3%=21(Uk(1,3)%+Uk(2,3)%−Uk(1,2)%)
那么就可以推出各侧绕组的漏电抗为:
X T 1 = U k 1 % U N 2 100 S N X T 2 = U k 2 % U N 2 100 S N X T 3 = U k 3 % U N 2 100 S N X_{T1}=\frac{U_{k1}\%U^2_N}{100S_N}\\\\ X_{T2}=\frac{U_{k2}\%U^2_N}{100S_N}\\\\ X_{T3}=\frac{U_{k3}\%U^2_N}{100S_N} XT1=100SNUk1%UN2XT2=100SNUk2%UN2XT3=100SNUk3%UN2
开路试验
通过同样的接法,试验得到三个结果,然后通过同样的算法,解出每一个绕组的断路电流百分数 I 0 % I_0\% I0%和断路损耗 P 0 P_0 P0。
然后通过计算得到:
G T = P 0 1000 S N S N U N 2 B T = I 0 % 100 S N U N 2 G_T=\frac{P_0}{1000S_N}\frac{S_N}{U^2_N}\\\\ B_T=\frac{I_0\%}{100} \frac{S_N}{U^2_N} GT=1000SNP0UN2SNBT=100I0%UN2SN
二三类变压器的折算
对于二三类变压器,一般设备提供的短路电压,都是已经折算过的,直接可以根据公式来计算变压器的参数。而对于没有折算过的短路电压,则需要根据容量来折算。
以第二类变压器(100/100/50)为例,因为短路的电压和电流成正比,而通过3侧的电流为其他侧的一半,所以电压也为一半,折算到变压器额定容量下的短路电压分别为:
U k ( 1 , 3 ) % = 2 × U k ( 1 , 3 ) ′ % U k ( 2 , 3 ) % = 2 × U k ( 2 , 3 ) ′ % U_{k(1,3)}\%=2\times U'_{k(1,3)}\%\\\\ U_{k(2,3)}\%=2\times U'_{k(2,3)}\% Uk(1,3)%=2×Uk(1,3)′%Uk(2,3)%=2×Uk(2,3)′%
自耦变压器等值电路
普通的变压器只存在磁路耦合,而自耦变压器则既存在磁路耦合,还存在电的联系。
如图所示:

k C = V 1 N V 2 N = J 2 N J 1 N = w 1 w 2 k_C=\frac{V_{1N}}{V_{2N}}=\frac{J_{2N}}{J_{1N}}=\frac{w_1}{w_2} kC=V2NV1N=J1NJ2N=w2w1
自耦部分:
k A = U 1 N U 2 N = V 1 N + V 2 N V 2 N = k C + 1 k_A=\frac{U_{1N}}{U_{2N}}=\frac{V_{1N}+V_{2N}}{V_{2N}}=k_C+1 kA=U2NU1N=V2NV1N+V2N=kC+1
总的容量为:
S A N = 3 U 1 N I 1 N = 3 ( V 1 N + V 2 N ) J 1 N = S C N + 3 V 2 N J 2 N k C = S C N ( 1 + 1 k C ) = S C N ( 1 + 1 k A − 1 ) S_{AN}=\sqrt{3}U_{1N}I_{1N}=\sqrt{3}(V_{1N}+V_{2N})J_{1N}=S_{CN}+\sqrt{3}V_{2N}\frac{J_{2N}}{k_C}=S_{CN}(1+\frac{1}{k_C})=S_{CN}(1+\frac{1}{k_A-1}) SAN=3U1NI1N=3(V1N+V2N)J1N=SCN+3V2NkCJ2N=SCN(1+kC1)=SCN(1+kA−11)