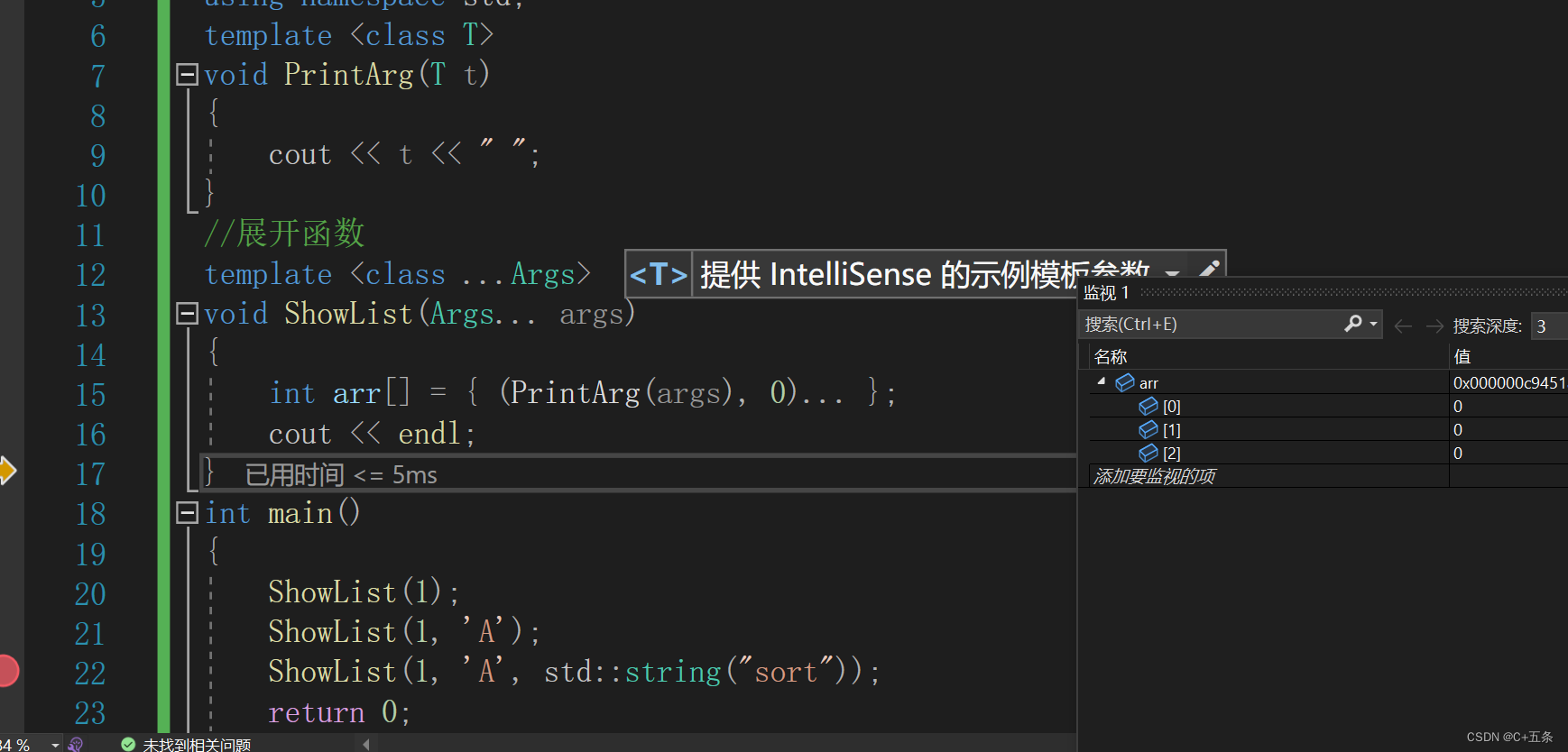
解非线性方程（Nonlinear Equations）的技术在其动机、分析和算法实现方面与优化技术（Optimization）有重叠。

相似点：

在优化和非线性方程中，牛顿法是许多重要算法的核心。诸如线搜索、信赖域和每次迭代中线性代数子问题的不精确解决方案等特征在两个领域中都很重要，还有其他问题，如导数评估和全局收敛。

诸如线搜索、信赖域和解决线性代数子问题等技术在解非线性方程和优化中起着至关重要的作用。这些方法有助于提高收敛速度、稳定性和效率。

非线性方程中的牛顿法

解 

采用了线性模型，在的Taylor展开中，只取了前两项（即进行一阶泰勒展开）。

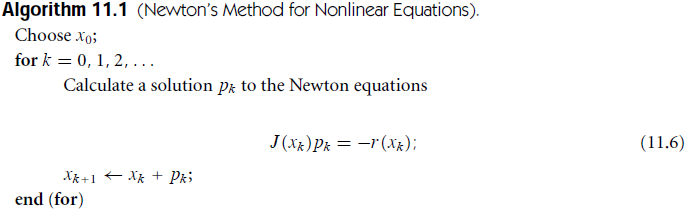
凸优化问题中的牛顿法

为了简单理解，以凸优化问题为例，求f(x)的极值点。

在凸优化问题中，局部最优即为全局最优。除了端点外，目标函数f(x)的极值点必有f'(x)=0。因此，凸优化问题可转化为求解f'(x)=0。

对f'(x)进行一阶泰勒展开

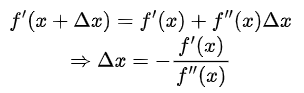
因此，迭代公式为

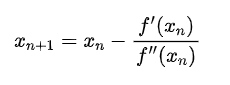
可以看出，优化问题中，实际上取了泰勒展开的前三项（即进行二阶泰勒展开）。

不同点：

1. 为了在优化问题中获得二次收敛，我们需要目标函数的二阶导数，而在非线性方程中，知道一阶导数就足够了。

2. 拟牛顿法在求解非线性方程组中可能不如在最优化问题中那么有用。

3. 线搜索和信赖域技术在最优化中起着同样重要的作用，但可以认为信赖域算法在解非线性方程组方面具有某些理论上的优点。

参考：

《Numerical Optimization》2nd Edition

学习笔记|凸优化问题中的牛顿法-云社区-华为云