2024.3.1|牛客周赛 Round 36

A.小红不想做炸鸡块粉丝粉丝题
B.小红不想做鸽巢原理
C.小红不想做完全背包（easy）
D.小红不想做完全背包（hard）
E.小红不想做莫比乌斯反演杜教筛求因子和的前缀和
F.小红不想做模拟题
G.小红不想做平衡树

心有猛虎，细嗅蔷薇。你好朋友，这里是锅巴的C\C++学习笔记，常言道，不积跬步无以至千里，希望有朝一日我们积累的滴水可以击穿顽石。

小红不想做炸鸡块粉丝粉丝题

题目：
小红作为炸鸡块哥哥的粉丝智乃的粉丝，做了一场炸鸡块哥哥的粉丝智乃的比赛后得出一个结论，那就是千万不要根据第一题的难度判断一场比赛的难度。
现在给定一场比赛6道题的难度，请你判断这场比赛是不是智乃style。
所谓智乃style，指第一题难度小于6道题难度之和的1/30。
输入描述:
六个正整数，用空格隔开。分别代表每道题的难度。
输出描述:
如果是智乃style，则输出"Yes"。否则输出"No"。
示例1
输入
200 1600 2200 2500 2800 3200
输出
Yes
示例2
输入
300 800 1000 1200 1800 2000
输出
No

注意：
A题是签到题。

实践代码：

void solve(){int a,b,c,d,e,f;cin>>a>>b>>c>>d>>e>>f;int sum=a+b+c+d+e+f;if(a<sum/30) cout<<"Yes";else cout<<"No";
}

小红不想做鸽巢原理

题目：
小红有n种不同颜色的小球，第i种颜色的小球有a_i个，放在同一个盒子中。
小红每次任意取出k个小球并丢弃，直到盒子中剩余的球数小于k个为止。
小红希望最终盒子里的小球颜色种类尽可能少，你能帮小红求出颜色的种类数量吗？
输入描述:
第一行输入两个正整数n,k，代表初始的颜色种类和小红每次丢弃的小球数量。
第二行输入n个正整数a_i，代表每种颜色的小球数量。
1≤n≤10⁵
1≤k,a_i≤10⁹
输出描述:
一个整数，代表最终剩余的颜色种类。
示例1
输入
4 2
1 2 2 4
输出
1
说明
小红可以操作4次，将第2、3、4三种小球全部丢弃。

注意：
B题先对每种球的个数排序，后按每种球的个数从小到大的每次丢弃k个

实践代码：

void solve(){int n,k;cin>>n>>k;vector<int> a(n);int sum=0,cnt;for(int i=0;i<n;i++) {cin>>a[i];sum+=a[i];}sort(a.begin(),a.end());//按每种球的个数从小到大排序if(sum%k==0) {cout<<0;return;}//如果恰好整除，说明丢弃k次正好能丢弃完(没有剩余)else{cnt=sum/k;//总共丢弃cnt次球(每次k个)int t=0;for(int i=0;i<n;i++){t+=a[i];//丢弃的前i种球的个数tif(t<(cnt*k)) a[i]=0;//如果t此时小于最多能够丢弃球的总数，那么将第i种球都丢弃掉else break;}}int f=0;//判断第i种球是否已全部丢弃完，不是则+1，说明此种球有剩余for(int i=0;i<n;i++){if(a[i]!=0) f++;}cout<<f;//输出剩余几种球
}

小红不想做完全背包（easy）

题目：
本题和hard版本的唯一区别是：p保证等于3。
完全背包是一个经典问题，但小红完全不会完全背包，因此她不想做完全背包。
现在小红拿到了一个长的很像完全背包的题，她希望你帮她解决一下。
给定一个背包，有n种物品，每种物品的价值为a_i​，有无穷多个。小红有一个无穷大的背包，
她希望往里面放若干个物品，使得最终所有物品的价值之和为p的倍数。
小红想知道最终至少要放多少物品？
（注意：不能不放物品）
输入描述:
第一行输入两个正整数n,p，用空格隔开。
第二行输入n个正整数1≤n≤2000
p=3
1≤a_i​≤10⁹
输出描述:
一个整数，代表小红最终要放的物品数量的最小值。
示例1
输入
4 3
1 2 3 4
输出
1
说明
小红只需要选择一个第三种物品即可。

注意：
C题，贪心+暴力枚举

实践代码：

void solve(){int n,p;cin>>n>>p;vector<int> a(n);for(int i=0;i<n;i++) cin>>a[i];sort(a.begin(),a.end());for(int i=0;i<n;i++) if(a[i]%3==0) {cout<<1;return;}for(int i=0;i<n;i++){for(int j=1;j<n;j++){//咔咔暴力咔咔就是干if((a[i]+a[j])%3==0) {cout<<2;return;}}}cout<<3;
}

小红不想做完全背包（hard）

题目：
本题和hard版本的唯一区别是：p没有必须等于3的限制。
完全背包是一个经典问题，但小红完全不会完全背包，因此她不想做完全背包。
现在小红拿到了一个长的很像完全背包的题，她希望你帮她解决一下。
给定一个背包，有n种物品，每种物品的价值为a_i​，有无穷多个。小红有一个无穷大的背包，
她希望往里面放若干个物品，使得最终所有物品的价值之和为p的倍数。
输入描述:
第一行输入两个正整数n,p，用空格隔开。
第二行输入n个正整数1≤n≤2000
p=3
1≤a_i​≤10⁹
输出描述:
一个整数，代表小红最终要放的物品数量的最小值。
示例1
输入
4 3
1 2 3 4
输出
1
说明
小红只需要选择一个第三种物品即可。

注意：
D题是一个典型的bfs+最短路径(二维数组存储)。

实践代码：

void solve(){int n,p;cin>>n>>p;vector<int> a(n+1),dp(p,INF);//dp[i]:选择的数对p取余等于i的最少选择数字个数for(int i=1;i<=n;i++) {cin>>a[i];a[i]%=p;dp[a[i]]=1;for(int j=0;j<p;j++){int ne=(a[i]+j)%p;dp[ne]=min(dp[ne],dp[j]+1);}}cout<<dp[0]<<endl;
}

小红不想做莫比乌斯反演杜教筛求因子和的前缀和

题目：
小红来到了一家蛋糕店，蛋糕店中售卖了若干种不同的长方体蛋糕，具体来讲，蛋糕店中售卖若干种形状为横向长度不大于n，纵向长度不大于m，高度不大于p个单位的蛋糕。每个蛋糕的表面要裹上奶油，也就是说，除了底面以外，其余5个面都需要裹奶油。我们不妨定义：奶油消耗量为暴露在空气中的5个面的面积之和。
我们定义两种蛋糕是不同的，当且仅当两个蛋糕的横向或者纵向长度或高度不同。即分别定义蛋糕横向的长度为i，纵向的长度为j，高度为k，则可以用三元组(i,j,k)表示蛋糕种类的唯一性。
现在小红希望你求出，共有多少种不同的奶油消耗量为x的蛋糕？
输入描述:
第一行输入四个正整数n,m,p,x，用空格隔开。
1≤n,m,p≤3000
1≤x≤10⁷
输出描述:
消耗量为x的蛋糕的种类数。
示例1
输入
2 2 2 8
输出
2

说明
如下图，共有以下两种蛋糕的奶油消耗量为8。

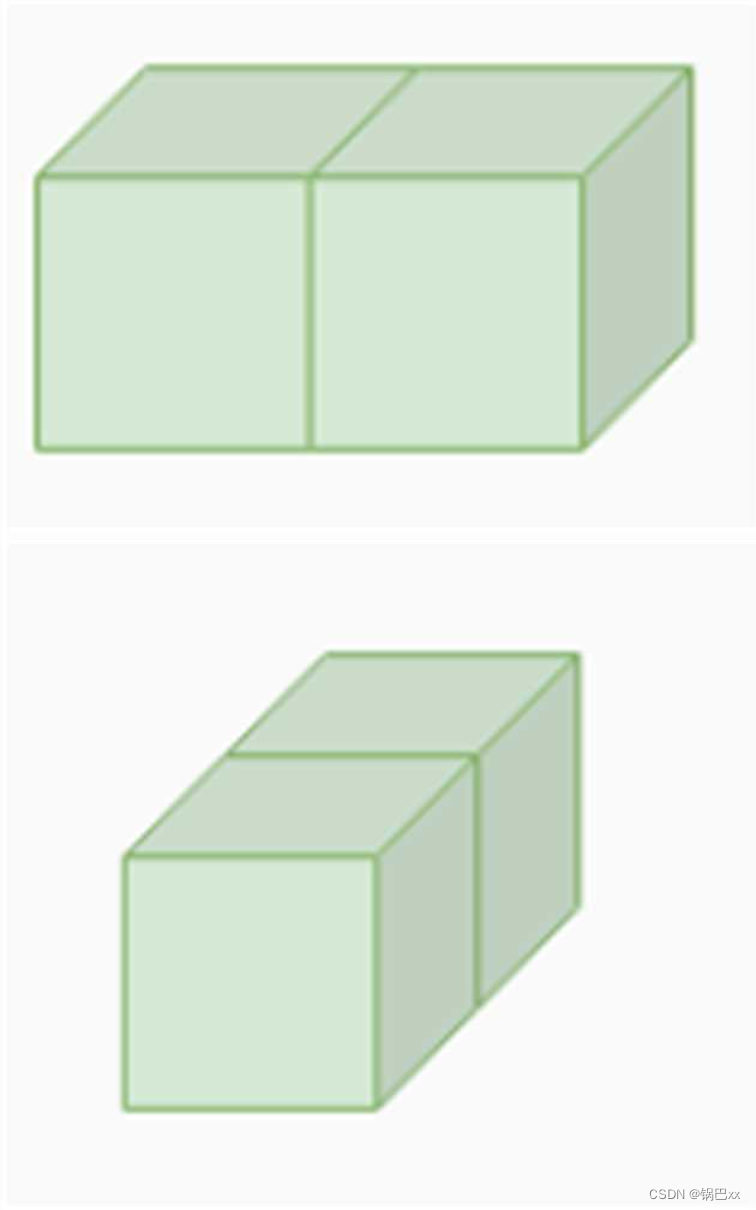
注意：
E题枚举长和宽即可，长和宽确定下来，高自然就固定了，接下来判断高是否大于p即可。

实践代码：

/** x = i*j+i*h*2+j*h*2 蛋糕的奶油量* x-i*j = 2*h*(i+j)* h = (x-i*j)/[2*(i+j)]  * */
void solve(){int n,m,p,x;cin>>n>>m>>p>>x;int ans=0;for(int i=1;i<=n;i++){//枚举长for(int j=1;j<=m;j++){//枚举宽if(x-i*j<=0) continue;int fz = (x-i*j),fm = (2*(i+j));if(fz%fm!=0) continue;int h=fz/fm;if(h<=p) ans++;}}cout<<ans;
}

小红不想做模拟题

题目：
给你两个长度大小为n的01串 A,B（指字符串的字符都为 '0’和 ‘1’ ）。
现在小红有若干次操作，每次选择一个01串的一个区间，将区间内所有字符都变成全1。
每次操作后，小红希望你求出两个字符串有多少个位置的对应字符都是1。用数学语言来说，即求${\sum }_{i=1}^n(a_i\&b_i)$。你能帮帮她吗？
输入描述:
第一行输入一个正整数 n，代表字符串的长度。
第二行和第三行分别输入一个长度为 n 的01串，分别代表A串和B串。
第四行输入一个正整数 q，代表操作次数。
接下来的 q 行，每行输入一个字符 c 和三个整数l,r，代表将对应字符串的第 l 个字符到第 r 个字符修改为 1。
1≤n,q≤10⁵
1≤l≤r≤n
c∈ ′A′,′B′
输出描述:
输出 q 行，每行输出操作后，两个字符串有多少个位置的对应字符都是1。
示例1
输入
4
0101
0110
2
A 2 3
B 1 4
输出
2
3
说明
第一次操作后，A字符串变成"0111"，有2个位置满足对应字符都是1。
第二次操作后，B字符串变成"1111"，有3个位置满足对应字符都是1。

注意：
F题数据水了，暴力即可。

实践代码：

void solve() {int n,q;string a,b;cin>>n>>a>>b>>q;int ans=0;for(int i=0;i<n;i++) ans+=(a[i]==b[i]&&a[i]=='1');while(q--){char c;int l,r;cin>>c>>l>>r;l--;r--;if(c=='A'){for(int i=l;i<=r;i++){if(a[i]=='0'&&b[i]=='1') ans++;a[i]='1';}}else{for(int i=l;i<=r;i++){if(b[i]=='0'&&a[i]=='1') ans++;b[i]='1';}}cout<<ans<<endl;}
}

心有猛虎，细嗅蔷薇。再见了朋友~